中考数学梯形压轴题解决策略

摘 要：数学作为初中阶段的主要课程，直接决定学生中考整体质量，受到广大师生的青睐。梯形压轴题作为数学试卷的重难点，也是令大部分学生头痛的所在。文中结合中考数学梯形压轴题特点，探讨如何做好这类题型的解答，提高解题质量与效率。

关键词：中考数学;梯形压轴题;解题思路

中考数学试题命制中梯形压轴题较为常见，通常会和几何图形、函数图像等内容结合起来，也有形式为动点的，全面考查学生综合运用能力。这就造成部分学生遇到这类题目后束手无策，白白失去大量分数。文中全面分析如何解决数学梯形压轴题。

一、 中考数学梯形压轴题的分析

（一）梯形压轴题特点

中考数学压轴题不是简单考查独立知识点的掌握程度，也不是如何运用某种解题思想与方法，而是对学生数学综合能力素养的考查，涉及非常多的数学知识点，全面运用各类数学思想方法，因此中考數学梯形压轴题特点：考查基础知识与技能的掌握;数学知识灵活运用能力;数学思维能力;数学研究能力的考查。中考数学试卷上压轴题分数较大，想要取得好的数学成绩，绝对不能忽略压轴题。数学教师已经意识到这点，中考数学复习时有意无意的加大压轴题的训练力度，但受到传统教育思想影响，师生都习惯题海战术，造成复习效果不理想。要想提高中考数学压轴题的复习质量，需要总结压轴题的特点，采取针对性的复制策略，提高数学梯形压轴题的解题效率。

（二）压轴题解题思路

梯形或等腰梯形问题解决时，要按照相应顺序进行：首先做好分类，分析时利用题目给出的已知条件，根据题意情况进行分类;其次画图，将符合题意的情况画出相应的图;最后完成计算，解决每一个画出图形的单位问题，解题时明白每种情况的都是相互独立的。

如果题干中给出一个三角形，解题时要从图形上找到第四个点，与三角形共同围成梯形，这时通过三角形定点做出对边平行线，移动这条平行线就能得到它与三角形的交点，这些交点与三角形其他顶点共同构成梯形，结合同位角、内错角等列出相应的方程;如果要解决一个等腰三角形，解题思路由梯形转为等腰梯形，根据“等腰梯形两边相等”，利用代数法或几何法证明两边相等即可。

二、 中考数学梯形压轴题的解决措施

已知直角梯形ASCD如图1所示，其中∠ABQ=90°，AD=24、BC=28，PQ两个动点分别从点A和点C出发，P点移动速度为1个单位长度/s、Q点移动速度为3个单位长度/s，前者运动轨迹为A-D、后者运动轨迹为C-B。如果有一个点抵达终点，另一个点也会停止移动。

求：（1）四边形PQCD从PQ两点开始运行时多久为平行四边形？

（2）四边形PQCD多久为等腰梯形？

解题思路：

这道题相对简单，解决P、Q两点运动时什么时候形成平行四边形与等腰梯形。但需要根据图形判断平行四边形、等腰梯形。如根据平行四边形的判定进行判断，在题干中找寻相应情况，并画出图形，最后表示出相应线段的长度，列出具体的方程。根据已知四边形ABCD是一个直角梯形，通过AD∥BC得到，只要证明PD=CQ即可;如果要根据等腰梯形判定，只需要得到两腰相等，罗列出相应的方程。

考虑到（1）问并不是研究重点，这里不做赘述，直接解决第（2）问。

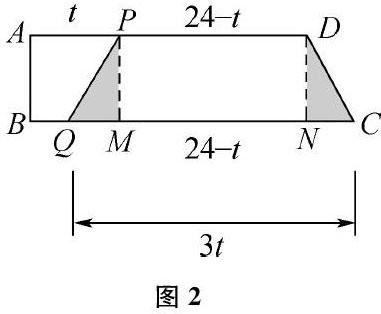
解：设经过t秒后四边形PQCD成为等腰梯形，如图2所示，直接经过P和D点作垂直BC的垂线，垂足标记为M、N，得到OM=CN，推出：AP=t，PD=24-t，CQ=3t，BQ=28-3t。

三、 教学反思

复习课上教师要做到创新，实现“反复而不重复”，避免学生出现审美疲劳，影响到复习课堂教学质量提升。

（一）重视知识迁移

复习课堂上要重视知识迁移训练，逐步淡化简单的知识再现，避免利用常见的问答式或学案填写方式展开教学，而是营造一个深刻的知识探究氛围，并将学生提出的问题达成骨架，系统解决问题，加强学生利用知识解决新问题的能力，巩固知识点。学生全部完成呈现出的知识结构，教师仅起到引导作用，加深其对知识点的理解。教师可以将同种题型进行归类。比如从易到难进行排列，将一些经典的并且高频率出现的题型归到一类，这样会让学生们更好地掌握其知识点，也会使自己在解决这些问题的时候也会具有一定的条理性。

（二）做好查漏补缺

问题在于学生如何找出知识漏洞。在平时讲课、做题、教师提问中，学生一定会出现一些错题，而对这些错题一定要引起重视，不能将其抛掷脑后，听之任之而不管不问，应该将他们抄录在错题本上，分析致错原因，有意识的记忆，保证不在同一个地方摔倒两次，这才是查漏补缺记忆法的正确用法。在开展数学复习时，教师需要参考《考试大纲》指引，同时结合近年来中考趋势变化，对学生开展专题复习，再利用问题法，引导学生借助问题进行深入复习，从而帮助学生养成针对问题的思考能力，鼓励同学之间开展交流和讨论，加深对知识点的理解与掌握，确保复习的有效性。在开展复习时，通过问题法引导学生进行高效复习，培养学生数学综合能力与素养。因为复习时间安排较紧，教师需要将专题中的主要内容以问题形式呈现给学生，加深学生记忆。

四、 结语

总之，中考数学梯形压轴题中以梯形或等腰梯形为主，虽然两者看似不同，但其中均隐藏着矩形，解题时巧妙使用隐藏矩形及相关性质，学生以此为基础做好总结分析工作，顺利完成总结与提炼工作，帮助其顺利解决数学压轴题，促进中考数学成绩的提高。

参考文献：

[1]郑宏周.中考数学梯形压轴题解决策略探究[J].中学数学，2020（8）：62-63.

[2]陈润凯，高志锋，杨随义.中考数学压轴题的竞赛数学背景溯源[J].数学教学研究，2012，31（9）：59-61.

[3]苗鑫，任北上，赵静静，等.中考数学压轴题中的双动点型问题解析[J].数学学习与研究，2012（13）：127-129.

[4]卢守平.中考数学压轴题的特点及策略[J].数学教学通讯，2012（13）：26-27.

作者简介：

谢激强，福建省泉州市，福建泉州安溪毓秀学校。