三种群竞争合作非局部扩散时滞系统行波解的存在性

姚美萍,乔鹏芝,王飏

(山西大学 数学科学学院,山西 太原 030006)

0 引言

近年来,如下带有时滞的三种群竞争合作反应扩散系统得到一定的关注[1],

(1)

其中,ui(x,t)表示3个种群的种群密度,di>0,ri>0, 0≤aij<1,τij≥0,i,j=1, 2, 3。事实上,可以看出,在系统(1)中,种群u1和u2相互合作并且同时与u3进行竞争。

(2)

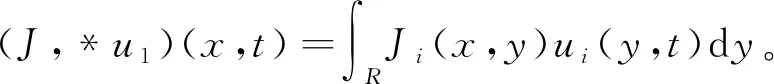
进一步,对系统(2)中的参数和核函数做出如下假设:d1=d2=d,a31k1+a32k2>1,且核函数Ji(i=1, 2, 3)满足

(P1)J1=J2=J;

本文将研究系统(2)连接平衡点E1和E2的行波解的存在性问题。

1 行波解的存在性

本节,我们考虑系统(2)行波解的存在性问题。事实上,如果向量函数

ξ=x+ct,ξ∈R,c>0,

且满足如下方程

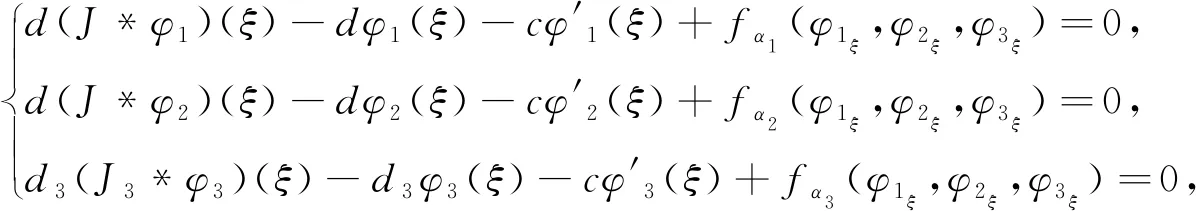
(3)

及边界条件

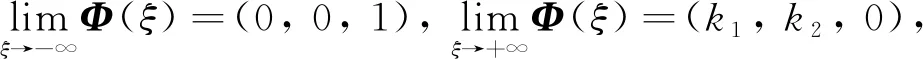
(4)

其中,

则称Φ(ξ)是系统(2)的连接E1和E2的行波解。

(5)

则系统(2)存在连接平衡点E1和E2的行波解对应于系统(5)存在连接平衡点(0, 0, 0)和(k1,k2, 1)的行波解。经变量替换后,边值问题(3)-(4)相应的转化为如下边值问题

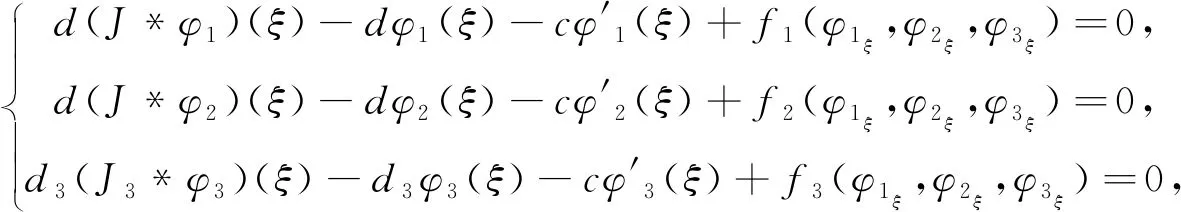
(6)

及

(7)

其中,

因此,我们只需证明边值问题(6)-(7)的解的存在性问题。

现在,我们给出系统(6)的上下解的定义。令

为了构造系统(6)的上下解,令

(8)

通过简单计算不难得到如下引理。

在本文中,我们给出如下假设:

(P4)r1(1-a13)=r2(1-a23)。

当(P4)成立时,由(8)式可知:

Δ1(λ,c)=Δ2(λ,c):=Δ(λ,c)。

进一步,引理1退化为下述推论。

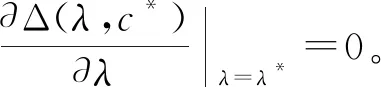
为方便起见,令

φiξ(s)=φi(ξ+s) (i=1, 2, 3),s∈[-cτ, 0],

τ=max{τij} (i,j=1, 2, 3)。

通过直接计算可得,当

β1>d+2r1k1+λ,β2>d+2r2k2+λ,

β3>d3+r3(1+a31k1+a32k2)+λ,

且τii=0时,函数fi(φ1,φ2,φ3) (i=1, 2, 3)满足文[5]所定义的拟单调条件(QM);

而当

β1>d+r1k1(eβ1τ11+1)+λ,

β2>d+r2k2(eβ2τ22+1)+λ,

β3>d3+r3(eβ3τ33+a31k1+a32k2)+λ,

且τii充分小时,函数fi(φ1,φ2,φ3) (i=1, 2, 3)满足文[5]所定义的弱拟单调条件(QM)*。

接下来,我们将通过两个引理证明,当c>c*时,如下定义的函数是系统(6)的上下解,

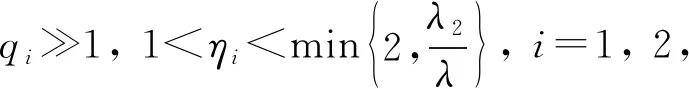
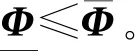
引理2 假设(P1)-(P4)成立,且满足

(9)

r3(a31k1+a32k2)≤r1(1-a13)。

(10)

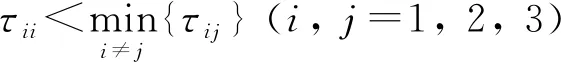
结合τ11<τ1j(j=2, 3),有

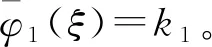
r1k1[1-a13-k1eλ(ξ-cτ11)+a12k2+a13eλ(ξ-cτ13)]=r1k1[k1(1-eλ(ξ-cτ11))-a13(1-eλ(ξ-cτ13))]。

令g(ξ,y)=k1(1-eλ(ξ-cy))-a13(1-eλ(ξ-cτ13))，当ξ=0时,

g(0,y)=k1(1-e-λcy)-a13(1-e-λcτ13)∶=h(y)。

当y=0时,

h(0)=-a13(1-e-λcτ13)<0。

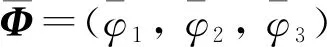
那么

dk1(eλξ-q1eη1λξ)-ck1(λeλξ-q1η1λeη1λξ)+r1k1(eλξ-q1eη1λξ)[(1-a13)-k1(eλ(ξ-cτ11)-q1eη1λ(ξ-cτ11))]≥

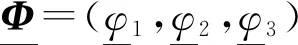
由引理1-3,我们可以得到本文的主要结论。

定理1假设(P1)-(P4),(9)-(10)成立,并且τii充分小或τii=0 (i=1,2,3)，当c≥c*时,对于系统(5),存在连接平衡点(0,0,0)和(k1,k2,1)的行波解Φ(ξ),且

(11)

证明当c>c*时,由文[6]及其参考文献易知,系统(5)存在连接平衡点(0, 0, 0)和(k1,k2, 1)的行波解。当c=c*时,由Helly定理[7-11]易知,系统(5)存在连接平衡点(0, 0, 0)和(k1,k2, 1)的行波解。接下来,我们讨论渐近行为。通过上下解的定义和函数的迫敛性可知

另外,

2 行波解的不存在性

定理2 当0

证明利用反证法讨论λ>0,c