R2中半线性椭圆型方程多解的存在性
张亚静,李巧琴,庞璐
(山西大学 数学科学学院,山西 太原 030006)
0 引言
我们研究以下半线性椭圆型方程:

(1)
其中Ω是R2中一个光滑有界区域,g∈C0(Ω)是一个非负且不恒为零的函数,λ≥0,γ≥0,函数f满足次临界增长条件。f在+∞处满足次临界增长条件是指对一切β>0都成立
f在-∞处满足次临界增长条件可类似定义。
近年来,很多人研究与问题(1)相关的方程:
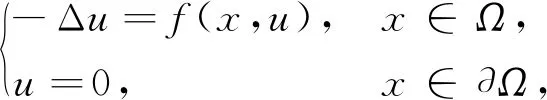
(2)

当空间维数N≥3时,具有物理与几何背景的方程

(3)
自从20世纪80年代以来得到了广泛研究。Brezis和Nirenerg在他们著名的论文[11]中指出该问题解的存在性不仅依赖于λ,而且与空间维数N有密切关系。邓引斌[12]以及朱熹平等人[13]研究了下面的非齐次问题

(4)
受到以上研究工作的启发,我们研究问题(P)γ。设函数f满足:
(H1)f∈C1(R,R),f(0)=f′(0)=0,f(t)t≥0,∀t∈R;
(H2)f(t)-f(s)>f′(s)(t-s),∀0≤s
(H3)存在独立于f的常数α>1,使得αf(t)≤f′(t)t,∀t≥0;

这些假设条件相对比较简单, 比如(H3)是著名的Ambrosetti-Rabinowitz类型的条件,(H4)也是很常见的条件。

则称u是问题(P)γ的一个解。
我们获得如下的结果。
定理1 假设函数f在±∞处满足次临界增长条件。对任意的λ∈(0,λ1),存在一个正数γ*使得当γ∈(0,γ*)时,问题(P)γ存在一个正极小解(极小解的定义将在第1节给出);当γ∈(γ*,+∞)时,问题(P)γ不存在正解。
定理2 假设函数f在±∞处满足次临界增长条件。对任意的λ∈(0,λ1),γ∈(0,γ*)(即定理1中的γ*),问题(P)γ至少存在两个解。
1 第一个解的存在性
本节将使用单调迭代法证明第一个解的存在性。
由于函数f具有次临界增长,故存在常数C和β使得
|f(t)|≤Ceβt2,∀t∈R。

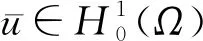
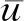

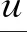

证明由条件(H4)可知存在常数C>0使得
再由条件(H3)可知
(α+1)F(t)≤f(t)t, ∀t≥0。
因此
取C1=-mint≥0[f(t)-(λ1-λ)t],我们可得
f(t)≥[λ1-λ]t-C1, ∀t≥0。
(5)
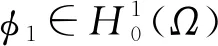
于是
因此
由(5)式可得
故

引理2 对任意λ∈[0,λ1),当γ充分小时, (P)γ至少存在一个正解。
证明既然f′(0)=0,那么存在ε>0使得
f(εφ1(x))<[λ1-λ]εφ1(x), ∀x∈Ω。
令
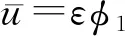
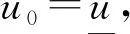
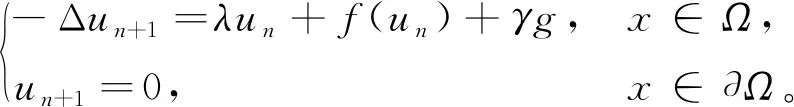
(6)


(7)
由(6)可得

(8)
类似地,由(7)可得

(9)
从(8)中减去(9)并且令ψ=(u1-w1)+,我们得到
因此ψ=0,于是u1≤w1在Ω上几乎处处成立。
类似地,由上、下解的定义以及(6)和(7),我们可以证明u0≤u1且w1≤w0。
我们接着使用归纳法来证明:un≤un+1≤wn+1≤wna.e.x∈Ω,∀n=0,1,2,…当n=0时上式显然成立。归纳假设
un-1≤un≤wn≤wn-1a.e.x∈Ω。
由(6)和(7)可得

(10)

(11)

因此un+1≤wn+1a.e.x∈Ω。 类似地我们可以证明un≤un+1以及wn+1≤wn。
由前面的两个结论可知
令
显然,u(x)≤w(x)a.e.x∈Ω。在(10)中取ψ=un+1可得

在(10)中令n→∞可得
类似地可知w也是(P)γ的一个弱解。然而,我们并不知道二者是否是两个不同的解。

un≤U≤wn, ∀n。
令n→∞可得
u≤U≤w,

(ii)当γ充分小时,引理2所得到的解实际上是(P)γ所有正解中的一个极小解。
引理3 对λ∈[0,λ1),存在正常数γ*使得当γ∈(0,γ*)时,(P)γ至少存在一个正解;而当γ>γ*时,(P)γ无正解。
证明令
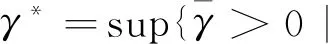
(P)γ都存在至少一个正解}。
由引理1和引理2可知γ*的定义是合理的。
任意取定γ0∈(0,γ*),我们取δ>0使得γ0+δ<γ*,设uγ0+δ是(P)γ0+δ的一个解。易知0是(P)γ0的一个下解并且uγ0+δ是一个上解。运用与引理2证明过程同样的方法可以得到(P)γ0的一个解uγ0,由注1可知uγ0是一个极小解。
再由类似的方法可知当γ>γ*时,(P)γ无正解。
引理4 假设λ∈[0,λ1),γ∈(0,γ*),其中γ*在引理3中定义。再设uγ是(P)γ的极小解,则
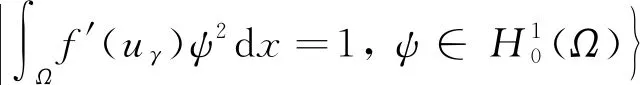
(12)
可以达到且τ>1。

因此|ψn|2是有界的。既然

因此当n→∞时,
由Lebesgue控制收敛定理可得
因此ψ0达到τ。显然|ψ0|也可以达到τ,所以不妨假设ψ0≥0,x∈Ω, 由Lagrange乘子法可知

(13)

(14)
由(13)和(14)可得
因此τ>1。
引理5
其中,
S={uγ|γ∈(0,γ*)},uγ是(P)γ的一个极小解。
证明对任意uγ∈S,由引理4可知
于是

(15)
显然

(16)
由(15),(16)以及条件(H3)可知
既然
我们得到
此处δ>0充分小且满足
因此存在仅依赖于λ1,λ,α,γ以及g的正常数C2使得
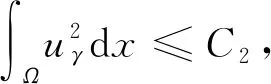
(17)
由(16)和(17)可得
因此存在独立于γ的正常数C使得
‖uγ‖≤C。
(18)
现在我们证明定理1。
假设γjγ*且uγj∈S,由引理5可知存在一个序列,不失一般性,仍记为{uγj},使得在中uγj弱收敛于u*,在L2(Ω)中uγj→u*,uγj(x)→u*(x)a.e.x∈Ω,易知u*是(P)γ*的一个解。对任意γ≥0,0都是(P)γ的一个下解。因此我们可以使用单调迭代法获得一个极小解。
2 第二个解的存在性
我们引入下面的问题
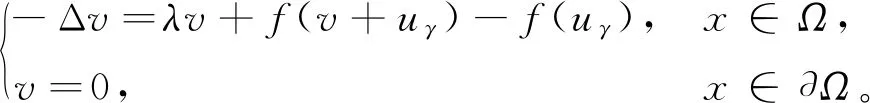
(19)
为了获得(P)γ的第二个解只需证明(19)存在一个非平凡解。这样uγ+v就是(P)γ的第二个解。

引理6 假设f具有次临界增长,那么J满足Palsis-Smale条件。

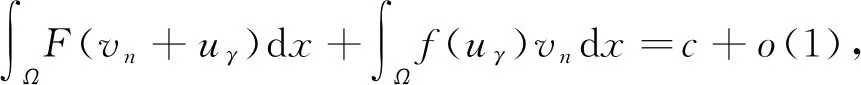
(20)
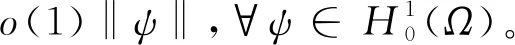
(21)
由条件(H1)和(H4)可知对任意ε>0都存在tε>0使得
F(t)≤εf(t)t, ∀|t|≥tε。
(22)
既然f具有次临界增长,故
|f(t)|≤Ceβt2, ∀t∈R。
(23)
由(20)和(21)可知

(24)
在(21)中取ψ=vn+uγ可得
o(1)‖vn+uγ‖=

(25)
将上面的不等式代入(24)可得
c+o(1)≤Cε‖νn‖+C。
既然

(26)
利用(23)以及和文献[16]中(3.9)相同的原因,我们可得存在q>1以及常数C′使得
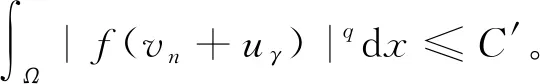
(27)
(21)减去(26)并且令ψ=vn-v可得
o(1)‖vn-v‖。
既然
|f(vn+uγ)-f(v+uγ)|q|vn-v|q′≤
2C′|vn-v|q′→0,
可得

令
h(x,t)=f(t+uγ(x))-f(uγ(x))-f′(uγ(x))t,

则
引理7 对λ∈[0,λ1),γ∈[0,γ*),问题(19)存在非平凡解。
证明我们首先表明存在η>0,ρ>0使得对‖ν‖=η,成立
J(v)≥J(0)+ρ。
(28)
由中值定理可得
h(x,t)=f(t+uγ)-f(uγ)-f′(uγ)t=
f′(uγ+θt)t-f′(uγ)t, (0<θ<1),

于是,存在δ>0使得
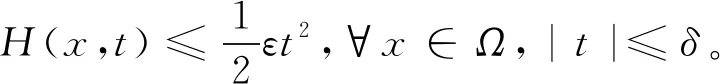
(29)
由(23)可得对q>2,成立
H(x,t)≤Ce2βt2|t|q,∀x∈Ω,|t|≥δ。
(30)
由(29)和(30)可得

(31)
于是,由Trudinger-Moser不等式可得
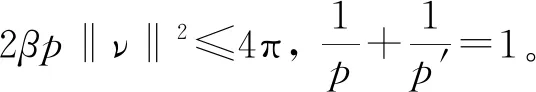
J(v)-J(0)=
因此如果我们取‖ν‖=η充分小,则(28)成立。

(32)
由条件(H1)和(H4)可知存在常数C3>0使得
于是,存在正常数C4和C5使得
F(t)≥C4|t|p-C5, ∀t∈R。
因此
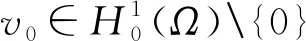
这样我们就验证了(32)成立。
应用山路定理(参见文献[17]中定理4.8.5)引理得证。
由引理7立刻证明了定理2。

