基于学生能力发展的 初中数学复习课实践探索

陈国兴 陈惠增

[摘  要] 文章从课堂教学的实用性角度来探讨目前复习课堂中的突出问题，并从课本中的基本图形、基本模型以及数学活动出发，以点带面，整合提升，把部分零散的知识点串联成整体的问题串，以达到提升数学复习实效性与有效性的目的.

[关键词] 复习;实效;感悟;变式;演变

数学复习课对于初中学习来说是一个重要的课型，是教师为了不让学生所学的知识遗忘而进行的数学课堂活动之一. 课堂复习的目的是让学生所学的知识得到巩固、解决问题的能力得到提升，并站在更高的角度思考问题，因此它的重要性不容小觑. 一节效率高的数学复习课要巩固所学知识，优化解题方法，渗透数学思想方法，提升解题效率. 下面，笔者针对复习过程中的一些问题与困惑，谈几点探索与创新的尝试.

问题的提出

多数数学复习课采用教师为主的课堂模式，教学顺序基本按照“知识点罗列——例题讲评——练习巩固”的方式进行. 这样的复习模式优点虽然较多，但具体的教学中却发现学生的收获很少，课堂中忽视了学生的主体地位，忽略了学生是学习的主人，而且知识的呈现过于直接，呈现的方式都是点状的，无法以点带面，缺乏知识来源过程的领悟;解题方法比较单一，缺乏总结、缺少深度. 这样的复习课教学模式局限于老、旧例题的反复出现，以及关键知识点的顺序罗列，容易陷入“题海”，容易让学生觉得课堂乏味，而且课堂的收获较低，不利于学生能力的培养以及数学素养的提升，复习效率低下.

提高数学复习实效的探索

新课程理念下的数学复习课教学过程，应注重学生在课堂教学过程中的主动参与和积极探索，应引导学生感悟解题方法，发现并挖掘重要知识的内涵与外延、变式与拓展，指导学生总结与归纳结论和方法，演变与创新教材中的数学活动资源，鼓励学生一题多解、一问多思、一图多变、多图化一、多解归一，使所有教学内容的应用性与实用性都得到落实. 要注重学生课堂学习的状况，形成学生内化的知识结构和内生的意识能力，把提高学生解决问题的策略当成课堂的总要求，促进其思维能力、数学素养等方面的发展.

1. 发现并挖掘核心知识、核心问题的内涵

数学复习课应让学生主动参与知识梳理的过程，发挥学生的潜力，让其带着问题思考，感悟所学知识点之间错综复杂的关联，理清它们的区别. 初中很多知识点，其核心知识是相似的，学习方法也是相通的，这样的学习完全可以通过类比的方式完成. 如整数与分数、整式与分式、整式方程与分式方程、方程与函数等. 在教学中，教师应引导学生发现相通知识的内涵，感悟知识间的联系，揭示关联知识的本质，引导他们高角度高方位地看问题，挖掘知识背后的关键内涵.

比如，复习“二次函数的图像与性质”时，可以引导学生体验如下过程：

针对方程x2-3x+2=0，预设如下问题：

（1）要求出此方程的根，你有哪些方法？

（2）在不求解方程的前提下，可以判断这个方程的根的情况吗？

在以上两个问题的基础上，可以借助与之相应的函数的图像来解答如下问题：

（1）画出抛物线y=x2-3x+2与直线y=0的图像，观察两个函数图像的交点，你有什么发现？

（2）若变为抛物线y=x2-3x与直线y=-2的图像呢？

（3）若再變为抛物线y=x2与直线y=3x-2的图像呢？

（4）若改为直线y=x-3与双曲线y=-■的图像呢？

（5）进一步探究方程x2-3x+2-■=0与方程x2-3x+2-■=0的根的情况.

学生在积极主动观察图像的过程中发现方程与函数的本质是一样的，感受到了方程与函数之间存在着千丝万缕的联系，领悟到了一次函数、二次函数、反比例函数的图像特点与方程之间的关系. 通过多角度的思考，学生归纳、总结了解决此类问题的策略，同时对各知识点进行了相应的补充，最终提升了自己各方面的能力. 复习中多以互相联系的知识点为载体，能让学生不断地联想、感悟、体验，从而达到比较理想的学习效果.

2. 变式与拓展同一背景、同一模型的问题

复习课中，若再将新课所学的知识一成不变地重复出现，将不容易激发学生思维的火花，不利于调动学生参与课堂的主动性，学生会无法体验到学习的新鲜感与成就感. 因此，在教学过程中，应不断地对问题进行变式、拓展、整合，应将新、旧知识点串成问题串. 教师进行教学预设时，无法把握生成的结果，因此应关注如何整理复习资料，选择典型案例，激发学生积极参与课堂活动的热情，课后不断反思，使复习课堂的有效性得以保证.

如初中的最值问题可做如下变式拓展.

探究：（1）已知A，B两点在直线a的同侧，如图1，在直线a上找一点M，使MA=MB.

（2）若A，B两点在直线a的异侧，能否在直线a上找到一点N，使AN+BN最短？若A，B两点在直线a的同侧，能否在直线a上找到一点M，使AM+BM最短？

（3）已知A，B两点在直线a的同侧，能否在直线a上找到一点G，使△AGB的周长最短？

（4）已知A，B两点在直线a的同侧，能否在直线a上找到一点D，使DA-DB最长？

（5）已知A，B两点在直线a的异侧，能否在直线a上找到一点E，使EA-EB最长？

（6）已知A，B两点在直线a的同侧，请在直线a上找一点P，使△PAB是直角三角形.

（7）已知A，B两点在直线a的同侧，请在直线a上找到一点Q，使△QAB是等腰三角形.

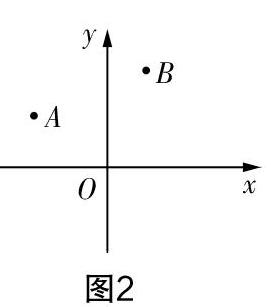
（8）如图2，若把直线a看作x轴，建立适当的坐标系，问题将变得新颖.

以上问题以“两点一线”为背景建立模型，引导学生在变化的过程中发现基本的几何模型（如“K”形图，“X”形图）. 复习时可以借助几何模型的结论，探讨解决基本模型的通性通法，从而利用几何图形的结论解决几何压轴问题. 对一些较常用的模型做变式处理，能引导学生归纳与总结某类题的通性通法，能激起学生强烈的参与热情与求知欲望，从而进行有效复习.

3. 指导学生研究归纳的方法

课堂45分钟的复习时间有限，所以课堂上应尽量避免出现下列情况：教师包办、学生独立思考时间短;练习量足够多，但解题能力却不见提升. 教学中，教师应指导学生研究、归纳解题方法，提升他们对同一系列问题的理解程度，同时在教师的指导下开展研究活动，让学生成为复习课中的主人，而不是观看者.

如复习平移、旋转、轴对称、位似这四个变换时，可以启发学生研究下列问题：

（1）先归纳点（x，y）左右平移和上下平移后坐标变化的规律，再研究二次函数图像的平移规律，以及一次函数、反比例函数图像的平移规律. 如二次函数y=3x2向左平移4个单位长度后的函数解析式是什么？一次函数y=3x向左平移4个单位长度后的函数解析式是什么？双曲线y=-■向左平移4个单位长度后的函数解析式是什么？

（2）再如旋转，引导学生先归纳一个点关于原点对称的坐标变化规律，再指导研究：若原点改为其他任意点呢？对称后的坐标应如何变化？若一个点绕原点顺时针旋转90°、270°后坐标应如何变化？你发现了什么新的规律？抛物线y=3x2的图像关于原点中心对称的图像是怎样的？解析式是什么？直线y=3x-2关于原点中心对称的图像是怎样的？解析式是什么？双曲线y=-■关于原点中心对称的图像是怎样的？解析式是什么？

（3）再如轴对称，引导学生先归纳一个点分别关于两条坐标轴对称的坐标变化规律，然后研究一个点关于直线y=x（或直线y=-x）对称的坐标变化规律.

学生在上述活动中不仅复习了这几个变换的特点和规律，更通过“函数图像的变换研究”对问题有了新的发现与认识. 这种“研究”方式将影响学生今后思考问题的方式.

4. 创新使用教材中实验观察与数学活动类资源

教材中各个章节后面都提供了“数学活动”“阅读与思考”以及“实验与探究”等资源. 近几年，各省市中考题经常将教材中的这些资源作为背景来命题，因此我们在复习时可以挖掘课后实验与探究以及数学活动的内容，将这些素材进行变式处理，从而深度理解教材，让学生站在更高的角度看问题，顺畅地进行数学探究活动.

如人教版八年级下册第63页实验与探究“丰富多彩的正方形”（稍做修改）：如图3，有两个完全相同的正方形ABCD和正方形OEFG，且正方形OEFG的顶点O与正方形ABCD的对角线交点重合. 可以发现，不论正方形OEFG绕点O如何旋转，两正方形重叠部分的面积始终等于正方形ABCD面积的■，请说明理由.

接下来，可对上述问题做如下演变与创新：

（1）旋转正方形OEFG的过程中，哪些量始终不变？

（2）如圖4，连接MN，GE，探究MN与GE的数量关系与位置关系，并说明理由.

（3）若AB=a，试探究两正方形重叠部分的面积S与a之间的函数关系式;重叠部分的周长会随着正方形的旋转而改变吗？

（4）如图4，设BN=x，△MON的面积为y，试确定y与x的函数关系式，并求出y的最大值或最小值.

（5）如图5，若改为点O与点A重合，猜想上述结论有哪些依然正确.

（6）若把上述两个正方形变为形状一样的两个正三角形或者正六边形，你会得到什么新的结论？

在以上探究活动中，教师应让学生体会任意正多边形在旋转过程中的不变性，体会动态几何中隐藏的“不变量思想”与“方程函数思想”. 教材中的很多材料都可以作为这样的素材进行变式与创新，体现了教材编写组独特的意图，以及数学课本独有的魅力. 教学中，我们应慢慢体会编写教材专家们的“编写初心”，领悟数学学习的本质内涵以及数学思维的发散本色.

反思与感悟

复习时切忌贪多求全，急功近利，要循循善诱，充分考虑到不同学生的个性差异以及认知结构，要关注复习过程中的知识关联，以及学生的能力提升，要努力反思学生的学习收获以及学习体验，及时引导学生去发现、去归纳，让问题在尝试和互动中生成. 我们要交给学生解决问题的思路与方法，要达到讲一题、通一类，使所有的解题策略达到“一通百通”的效果. 复习时，只要留给学生充裕的思考时间，让他们主动质疑、反思，领悟解题策略，领会数学方法，掌握数学思维，就能让他们在感受成功的同时体会学习的乐趣，养成勇于质疑、敢于创新的思维品质. 如讲解完一道综合题后，不要马上讲下一题，应留几分钟时间让学生反思，让学生从自己的视角来重新看这道题，这样他就会有新的发现;复习时应分段进行，复习完一段后，先让学生反思这一段的得失，总结方法，歇一歇，目的是为了更好地前行.

有效复习是一种教学理念，更是成功的方向，只要我们立足教材，抓住基本模型，对教材例题进行有效的变式，就会激发学生不断地进取与探索;为了提高数学复习的实用性与有效性，我们应该坚持以先进的教育理念为引领，大胆探索，勇于实践，不断改进，创新求变.