培养数学阅读方式的教学实践探讨
韩荣


[摘 要] 文章概述数学阅读的特征,并结合案例探讨阅读的不同方式——领悟式数学阅读、释疑式数学阅读、批判性数学阅读,认为数学阅读的作用是其他教学方式所无法代替的. 通过不同的数学阅读方式,学生能形成数学概念,理解数学原理,进而掌握数学思想,形成数学素养.
[关键词] 初中数学;数学阅读;实践
学生具备一定的数学知识与技能、经验与观念,是完成教学任务的必备条件,当这些条件不具备时,数学阅读是最好的方式. 数学阅读素养是生成学生其他素养的基础,只有学生拥有了数学阅读素养,其他素养才可以通过自身的努力逐步完善.
数学阅读的特征
不同的学科语言决定了不同的学习方式,阅读数学材料与阅读文史类材料不同,由于数学知识具有结构的严谨性、语言的精确性及理论的逻辑性,所以,学生在进行数学阅读时要讲究精确,要做到有条理,才能有所收获. 所以按顺序逐字逐句地阅读是数学阅读的第一个特征.
要表述一个完整的数学知识,除了文字之外,还必须使用数学语言,即数学符号、几何图形、图形表格等,这就需要学生理解每个数学语言的精确含义. 数学语言的精确性决定了文字语言不容许有含蓄、产生歧义的情况,所以学生只有弄清每一个数学符号、几何图形时,才能理解数学概念、数学原理或一个解答过程. 所以咬文嚼字是数学阅读的第二个特征.
进行数学阅读时,必须集中精力,心无他念,才能弄懂数学书面材料的顺序、结构组成等. 如果学生对阅读这部分材料没有兴趣,没有意志力,那么就无法揭示数学材料中的数学思想,更不可能把数学思想转化为自己的知识与能力. 同时,学生在认知上有错误的认识,抑或有数学概念或原理的缺失,那么在阅读的过程中就会出现理解上的偏差,致使阅读活动无法进行. 所以,全身心地投入是数学阅读的第三个特征.
造成学生数学阅读障碍的原因主要有两个,一是以往学习数学知识上的欠缺或错误的认识;二是把数学中各个知识点孤立起来理解和认识,不能在脑海中形成知识结构体系,没有认识到一些数学知识都是若干个数学对象彼此联系、相互融合的结果. 所以数学知识的紧密联系是数学阅读的第四个特征.
数学阅读的不同方式
方式就是说话、做事所采取的方法与形式. 做任何一件事情,要想取得成功,都要講究方式方法,数学阅读也不例外. 要在数学阅读中取得成效,就要讲究数学阅读的方式方法. 那如何培养学生良好的数学阅读方式与方法呢?下面笔者与大家一起分享三种数学阅读的方式.
1. 领悟式数学阅读
进行数学阅读时,如果产生一个数学问题,那这个问题的解决需要经过一个思维过程,它包括分析与综合、演绎与归纳、抽象与概括. 虽然每个学生在每个环节所用的时间不尽相同,但这些环节都是必经的过程. 如果学生有一定的领悟能力,那对数学教材的理解只需要在感知活动中进行. 在感知活动中,可将新学习的内容与已有的概念、定理或解题思路进行对比,加工成个性化的内容. 领悟式数学阅读最重要的是应有求异之心,其有助于从平常的现象中发现意想不到的新知识,具有化腐朽为神奇的力量. 当然,学生的领悟能力因个体的知识量、学习经验不同而有所不同,进而会出现层次与水平的差异.
案例1?摇 “平面直角坐标系”教学片段.
师:你对坐标系这个概念有何认识?
生1:坐标系是为了确定平面内点的位置而创造出来的一种数学工具,与生活中电影院的座位、经纬网中的经度与纬度类似.
这是这位学生通过阅读数学教科书后对“坐标系”形成的深层次领悟,说出了坐标系概念的本质.
师:如何用坐标系确定平面内点的位置呢?
生2:过这个点分别作两坐标轴的垂线,垂足在横轴上的坐标就是它的横坐标,垂足在纵轴上的坐标就是它的纵坐标. 如图1所示,点P的坐标就是(-1,2).
师:如何根据点的坐标在坐标平面内找出对应的点呢?
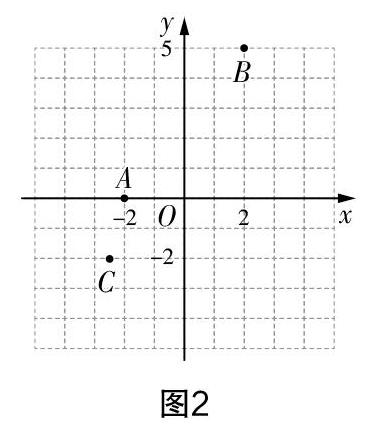
生3:在横轴上找到横坐标,过这个点作横轴的垂线,在纵轴上找到纵坐标,过这个点作纵轴的垂线,两条垂线的交点就是所要找的点. 如点A(-2,0),B(2,5),C(-2.5,-2)在平面直角坐标系中的位置如图2所示.
领悟式数学阅读对学生的要求比较高,学生要有创新精神,只有这样,学生才能由教科书的表象过渡到数学的结构性本质. 需要注意的是,在创新的过程中,学生要克服消极的心理定式,要增强自信心,这样才能居高临下地掌握数学知识.
2. 释疑式数学阅读
学生进行数学阅读时,可能由于经验不足,或阅读方法不对,不能深入到数学知识的本质结构,从而出现眉毛、胡子一把抓的情况. 如,忽略关键性词语、数学概念之间的结构关系. 在这种情况下,教师要在关键地方精心设计问题,促进学生对数学本质的理解,培养他们的理性精神.
案例2 “一元二次方程根的判别式”教学片段.
师:根的判别式是如何判定一元二次方程根的情况的?
生1:当Δ=b2-4ac>0时,一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根;当Δ=b2-4ac=0时,一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根;当Δ=b2-4ac<0时,一元二次方程ax2+bx+c=0(a≠0)没有实数根.
师:能不能将判定中的“实数根”换成“根”呢?
生1:……可以吧……不可以吧……(学生一时之间难以回答)
师:判定中的“实数根”不能换成“根”. 这是因为,当Δ=b2-4ac<0时,一元二次方程ax2+bx+c=0(a≠0)仍然有根,只不过是虚根,而这种情况,同学们将在高中阶段学到. 初中阶段,数的范围只限实数,当Δ=b2-4ac<0时,我们只能说这个一元二次方程没有实数根,而不能说它没有根.
师:当Δ=b2-4ac=0时,一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,此时可不可以说这个方程只有一个实数根?
生2:……可以吧……不可以吧……(学生一时之间又难以回答)
师:也是不可以的. 因为当一个一元二次方程只有一个实数根时,它可能还有一个虚数根,而当Δ=b2-4ac=0时,一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根. 也就是说,任何一个一元二次方程都有两个根,这两个根可能是两个实根,可能是两个虚根,也可能是一个实根一个虚根.
在实际教学过程中,学生往往会对新学习的定理或法则只掌握一个大概,而不能深刻地把握与理解,其关键是不能找出定理或法则中的关键词或核心词. 此时,教师要把这些关键词设计成问题,提出来让学生思考与讨论,以引起学生的重视和理解.
3. 批判性数学阅读
在阅读数学教材的过程中,学生应有质疑与批判的精神. 一方面,可以对教材所呈现的内容展开批判与质疑;另一方面,可以对自身的思维活动展开质疑与批判,即对運用知识经验理解新知识的过程展开质疑与批判. 笔者在教学实践中就有这样一个很好的案例.
案例3?摇 “角平分线”教学片段.
角平分线的定义:如果一条射线把一个角分成两个相等的角,那么这条射线就叫这个角的平分线. (大屏展示)
学生读完以后……
师:同学们,这个定义对吗?
生1:课本讲的还有错误吗?
师:请继续看下面两个图. (大屏展示)图3、图4所示的射线PC是∠AOB的平分线吗?
生2:不是. 但这两个图形却符合角平分线的定义,所以这里角平分线的定义是不够严密的.
师:那大家讨论一下应该如何定义.
同学们经过讨论、批判、质疑……最终得到角平分线比较严格的定义,即“以角的顶点为端点的一条射线,在角内部把这个角分成两个相等的角,这条射线叫这个角的平分线”.
阅读教材时,我们一方面要做到不盲从,不迷信权威,要让自己的阅读与思维具有创造性;另一方面,要深入理解事物的本质,改造自己的学习经验,不断审视自己的思维过程,让批判性阅读发挥独到的作用.
总结与反思
苏联斯托利亚尔认为,数学教学即数学语言的教学. 而语言的学习与阅读相依相随,数学阅读包含感知和认读、同化和顺应、理解和记忆等心理活动,是一个不断假设、证明、想象、推理的积极能动的认知过程. 教学中应重视数学阅读,因为其独特作用是其他教学方式所不能代替的. 学生在课堂教学中学习数学知识的时间是有限的,但预习、做作业、做试卷、做练习、网络学习都离不开数学阅读,所以只有通过数学阅读,学生才能最终接收数学知识,形成数学概念,理解数学原理,进而掌握数学思想,形成数学素养.

