绝对值二次函数的性质及应用

◇ 甘肃 吕兴金

形如f(x)＝|ax2＋bx＋c|(a≠0)的函数,称为绝对值二次函数.由于此类函数实际上是由二次函数y＝ax2＋bx＋c(a≠0)与绝对值函数y＝|x|复合形成的一个复合函数,所以我们可以利用二次函数的图象和性质作为出发点进行研究.

1 性质

二次函数y＝ax2＋bx＋c(a≠0)的判别式为Δ＝b2－4ac,当Δ＜0时,可得函数f(x)的图象,如图1；当Δ＝0时,可得函数f(x)的图象,如图2；当Δ＞0时,可得函数f(x)的图象,如图3.

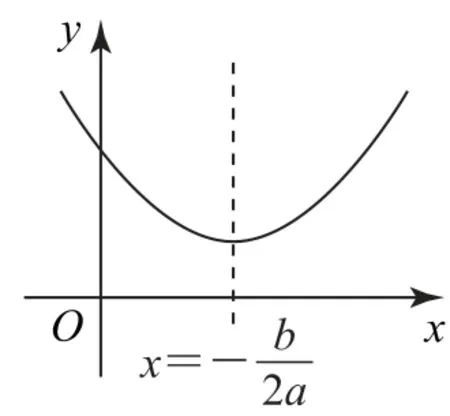
图1

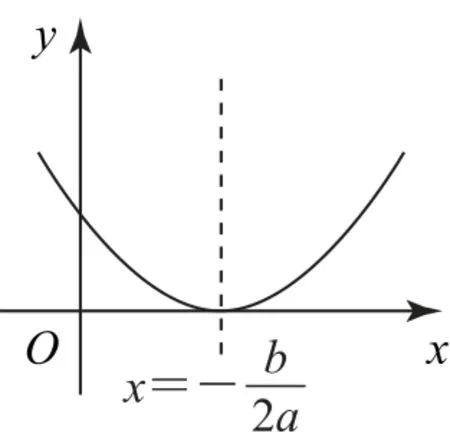
图2

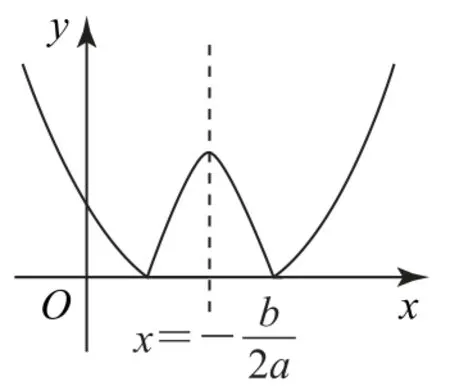
图3

结合上述图象,可得如下性质.

2)只有当b＝0时,函数f(x)才是偶函数；否则,函数f(x)既不是奇函数也不是偶函数.

2 应用举例

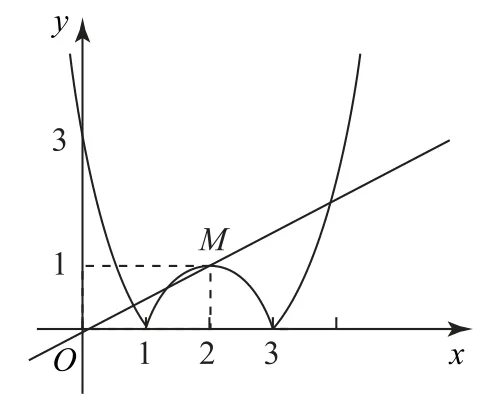
图4

①f(x)必是偶函数；

②当f(0)＝f(2)时,函数f(x)的图象必关于直线x＝1对称；

③若a2－b≤0,则函数f(x)在[a,＋∞)上是增函数；

④函数f(x)的最小值为|a2－b|.

其中正确命题的序号是____.

当f(0)＝f(2)时,因为|b|＝|4－4a＋b|,则a＝1或b－2a＋2＝0,由此易知命题②错误.当然,结合图3也可找到反例说明命题②错误.

若a2－b≤0,则二次函数y＝x2－2ax＋b 的判别式Δ＝(－2a)2－4b＝4(a2－b)≤0,所以结合图1、图2即知命题③正确.

因为当a2－b＞0时,结合图3即知函数f(x)的最小值为0,但此时|a2－b|＞0,所以命题④错误.

综上,正确命题的序号是③.

总之,本文主要说明了绝对值二次函数的概念、性质及其在解题中的灵活应用.显然,此类问题在知识交会点处设计,符合近年新课标高考理念,能够较好地培养学生在直观想象、逻辑推理以及数学运算方面的核心素养,故值得我们去关注和学习.