函数奇偶性的判定方法

◇ 山东 师吉芹

函数的奇偶性反映了函数图象的对称性,充分体现了“数”与“形”可以互相转化的思维.数形结合是进行数学分析和数学研究的有力工具,对函数部分的知识体系和综合应用具有纽带的作用,而正确快速判断函数的奇偶性是解决问题的关键所在.

1 定义法

利用函数奇偶性的定义进行判别时,要注意以下两点：

1)在整个函数的定义域内考虑；

2)具有奇偶性的函数,其定义域一定关于原点对称.

分析应该先求出函数f(x)的定义域,再对相应的解析式加以恒等变换后,利用定义判断奇偶性.

解函数f(x)的定义域为

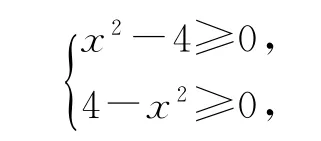
即x2－4＝0,解得x＝±2,所以f(x)的定义域为{2,－2},原函数可以恒等变形为f(x)＝0(x＝±2),此时f(－x)＝f(x)与f(－x)＝－f(x)同时成立,所以函数既是奇函数又是偶函数.

2 图象法

根据具有奇偶性的函数的图象特征,函数是奇(偶)函数的充要条件是它的图象关于原点(y 轴)对称.

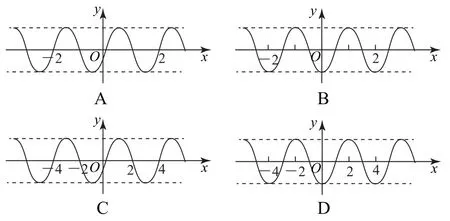
分析结合题目中给出的关系式确定函数所具有的奇偶性,再结合各选项中函数的图象确定各自相应的奇偶性进行综合判定.

解由f(－x)＝f(x),可知函数f(x)为偶函数,其图象关于y 轴对称,可以排除选项A 和C.

再利用f(x＋2)＝f(x),可知函数为周期函数,且T＝2,必满足f(4)＝f(2),可以排除选项D.故选B.

3 性质法

在各自函数公共定义域的条件下,偶函数与偶函数的和、差、积、商(分母不为零)仍为偶函数；奇函数与奇函数的和、差仍为奇函数；奇(偶)数个奇函数的积、商(分母不为零)为奇(偶)函数；一个奇函数与一个偶函数的积为奇函数.

A.f(x)g(x)是偶函数

B.|f(x)|g(x)是奇函数

C.f(x)|g(x)|是奇函数

D.|f(x)g(x)|是奇函数

分析结合函数的奇偶性所满足的关系式,根据奇偶性的定义,通过函数奇偶性的性质,利用排除法加以分析与判定.

解因为f(x)是奇函数,g(x)是偶函数,所以有f(－x)＝－f(x),g(－x)＝g(x),于是f(－x)·g(－x)＝－f(x)g(x),即f(x)g(x)为奇函数,选项A 错误.

|f(－x)|g(－x)＝|f(x)|g(x),即|f(x)|·g(x)为偶函数,选项B错误.

f(－x)|g(－x)|＝－f(x)|g(x)|,即f(x)·|g(x)|为奇函数,选项C正确.

|f(－x)g(－x)|＝|f(x)g(x)|,即f(x)·g(x)为偶函数,选项D 错误.

综上,故选C.

4 特殊变形法

对于抽象函数奇偶性的判断与证明问题,往往要对相应关系式进行变形,代入特殊值,以创新的角度结合函数奇偶性的定义来判断与证明相应函数的奇偶性问题.

分析可根据函数奇偶性的定义进行证明,应由条件先得到f(0)＝0后,再利用条件f(x1＋x2)＝f(x1)＋f(x2)中x1,x2的任意性加以变形,从而使结论得证.

证明对任意x,y∈R均有f(x＋y)＝f(x)＋f(y),若令x＝y＝0,则f(0)＝f(0)＋f(0),f(0)＝0,再令y＝－x,则可得f(0)＝f(x)＋f(－x),因为f(0)＝0,所以f(－x)＝－f(x),故f(x)是奇函数.

实际判断函数的奇偶性问题时,有时可单独使用其中的一种方法来处理,有时要用多种方法来综合处理.