一道椭圆中点弦问题的拓展与变式
2020-09-04 12:55王凯
高中数学教与学 2020年15期
王 凯
(甘肃省高台县第一中学,734300)

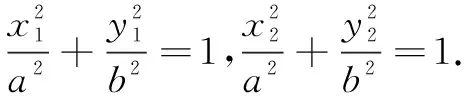


反思点差法是解析几何设而不求的常用解题方法.提炼上述解题过程,推广到圆锥曲线,不难得到如下拓展.


由结论1、结论2不难发现,在与椭圆或双曲线的中点弦相关问题中,中点弦所在直线的斜率、中点坐标、离心率这三个量中,已知其中两个量就可求出第三个量.由此,我们利用结论1、2就可以以点带面,迅速处理与中点弦相关的一类变式问题,有效避免题海战术,提高学习效益.下面以椭圆为例举例说明.

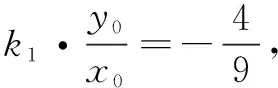





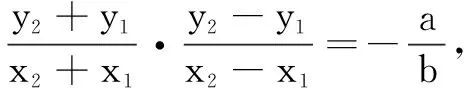

直线与圆锥曲线的相交位置关系中,往往能整合弦长公式、点到直线的距离公式、面积的表示,以及垂直、定值或最值等问题.与弦中点有关问题都可以用前面几种解法去尝试,体现设而不求、整体变换的思想,真正实现了代数与几何完美结合和化繁为简的目的.
猜你喜欢
第二课堂(初中版)(2022年5期)2022-05-24
新世纪智能(数学备考)(2021年5期)2021-07-28
中学生数理化(高中版.高考数学)(2021年4期)2021-07-20
甘肃教育(2020年18期)2020-10-28
甘肃教育(2020年22期)2020-04-13
甘肃教育(2020年20期)2020-04-13
甘肃教育(2020年12期)2020-04-13
学苑创造·C版(2018年3期)2018-05-28
电测与仪表(2016年5期)2016-04-22
新高考·高二数学(2014年12期)2015-10-16

