“五心”易解不易结——与三角形“五心”有关的解析几何题例析

潘振嵘

(江苏省木渎高级中学，215101)

三角形有重心、内心、外心、垂心和旁心,利用这“五心”构建的解析几何题,涵盖了代数、三角、几何等方面的知识,综合性强,方法灵活.现举几例加以说明.

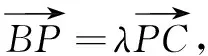
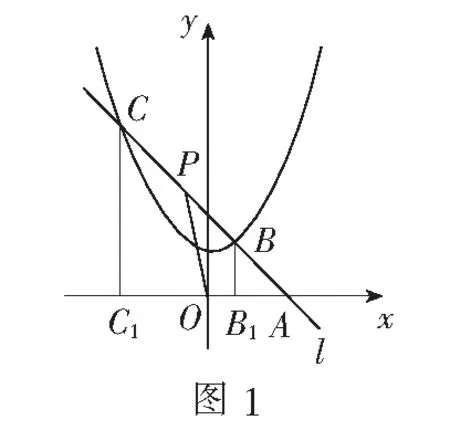
解设直线:y=k(x-2),其中k≠0.与抛物线方程联立,消去x,得y2+(4k-k2)y+6k2=0.

依题意,Δ=(4k-k2)2-24k2>0,即k2-8k-8>0,(k-4)2>24.

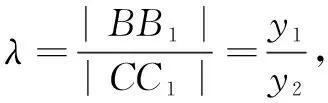
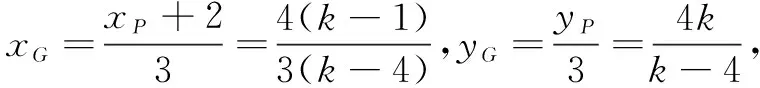
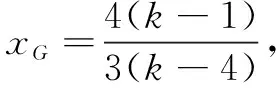
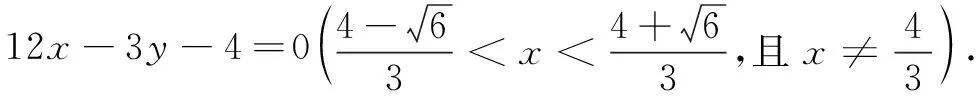
评注本题按自然思路,先由解析法求得点P的坐标,再由重心的坐标公式得到点G的坐标,消去参数可得轨迹方程.解题时对综合运算能力有较高要求,且轨迹方程要做到不重不漏.

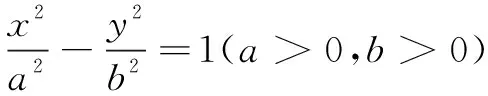
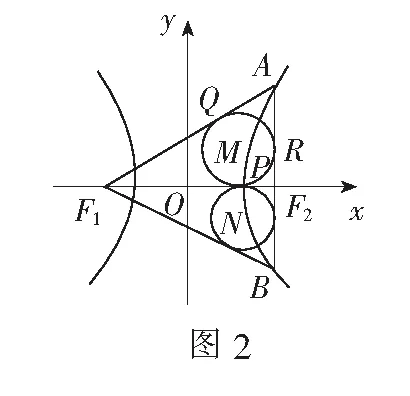
(1)若⊙M与F1F2相切于点P,求证:|PF1|-|PF2|为定值;

(2)连结MN,求MN所在直线的倾斜角;

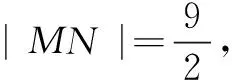
解(1)设⊙M分别与AF1与AF2切于点Q,R,则|F1P|=|F1Q|,|F2P|=|F2R|,|AQ|=|AR|.于是|PF1|-|PF2|=|F1Q|-|F2R|=(|F1Q|+|AQ|)-(|F2R|+|AR|)=|AF1|-|AF2|=2a(定值).

(2)由|PF1|+|PF2|=2c,且|PF1|-|PF2|=2a,解得|PF1|=c+a,|PF2|=c-a.

由点F1,F2在x轴上,O为F1,F2的中点,且|PF1|>|PF2|,可知点P在OF2上.又|OF2|=c,|PF2|=c-a,故点P的坐标为(a,0).结合MP⊥x轴,得点M的横坐标为a.

同理可证点N的横坐标也为a.于是MN⊥x轴,从而MN所在直线的倾斜角为90°.

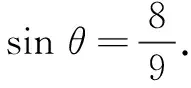
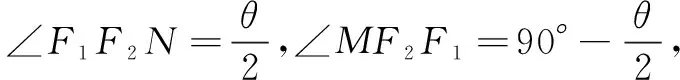
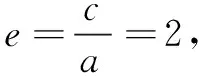
评注第(1)问需熟悉内接圆的几何性质,并与双曲线的定义综合解题;第(2)问需由(1)联想双曲线的定义得出点P为定点,再由圆的切线性质得出结论;第(3)问考查几何与三角的综合能力,对数形结合、方程思想的运用也提出了要求.

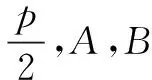
(1)建立适当的平面直角坐标系,求∆AMN的外心C的轨迹E;

(2)当∆AMN的外心C在E上什么位置时,使d+|BC|最小?最小值为多少?(其中d为外心C到直线c的距离)

解(1)如图3,以直线b为x轴,过点A且与直线b垂直的直线为y轴建立平面直角坐标系,则有A(0,p),B(2p,p).

设∆AMN的外心C(x,y),则M(x-p,0),N(x+p,0).由|CA|=|CM|,得x2+(y-p)2=(x-x+p)2+y2,化简得轨迹E:x2=2py.

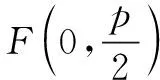
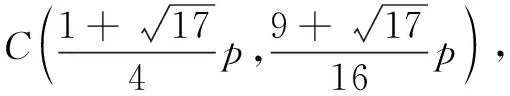
评注本题第(1)问需要合理建系,由外心的定义选择适当的路径解题,路径选择不唯一;第(2)问围绕抛物线的定义及经典几何最值设置问题,考查思维的灵活性.

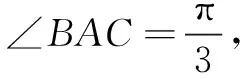
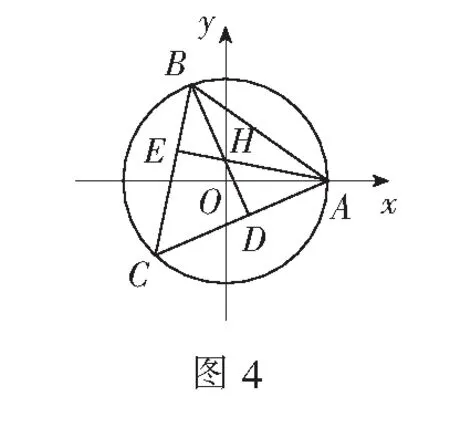
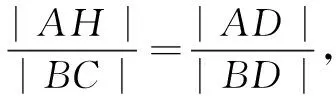
评注本题思维方向不易把握.解题时可由几个不同的特殊位置入手,在精准作图的基础上,先猜后证.