利用轨迹巧解三角形中的最值问题*

闫 伟

(广东省中山市濠头中学，528437)

笔者经调研发现,对于三角形中的最值问题,多数学生仍习惯于依赖复杂的运算和推理过程进行解题,解题效力不高.本文从轨迹的视角探求此类最值问题,不但能使问题得以巧妙解答,而且能很好地锻炼学生的思维能力,提升学生的数学核心素养.

一、 求角的最值

例1在∆ABC中,a,b,c分别为内角A,B,C的对边,已知a+c=2b,则角B的最大值为______.

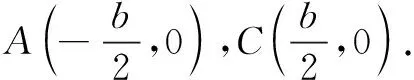
评注本题用余弦定理结合不等式可以求得结论,但是运算相对复杂;由条件联想椭圆定义,用椭圆的性质解题,过程简洁明了.

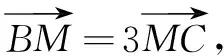
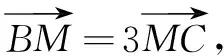
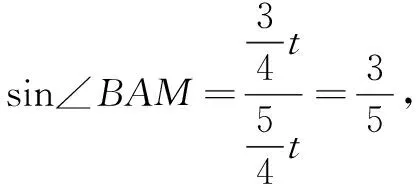
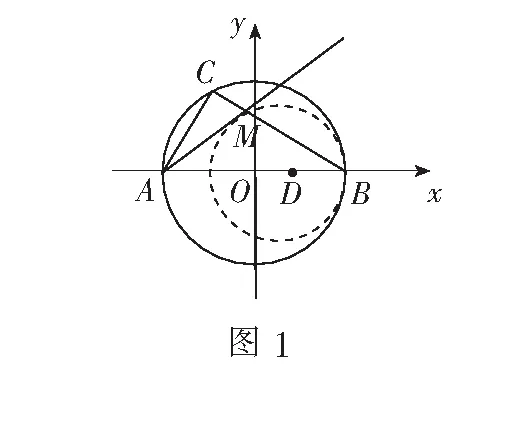
二、求边的最值或取值范围

例3在∆ABC中,a,b,c分别为内角A,B,C的对边,若c=2b,且∆ABC的面积为1,则边a的最小值为______.

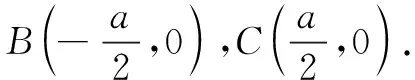
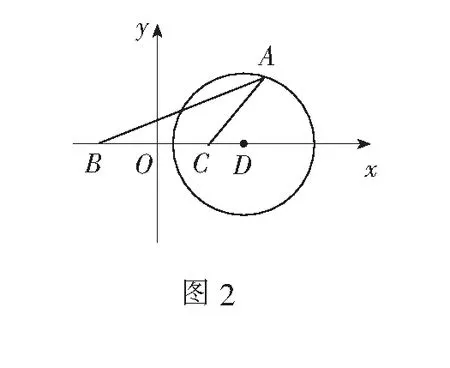
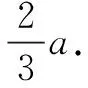
评注本题条件c=2b的几何背景为阿波罗尼斯圆,上述解答使问题求解更加直观形象,体现了数形结合的优越性.

例4在锐角∆ABC中,BC=2,sinB+sinC=2sinA,则中线AD长的取值范围为______.

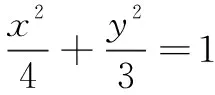
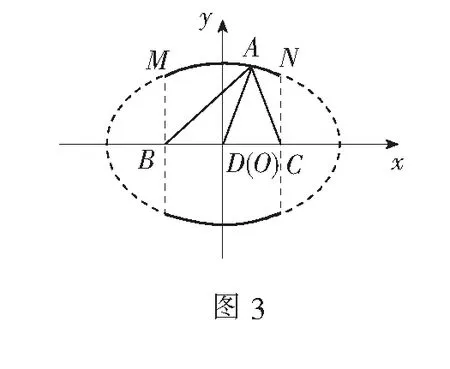
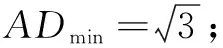
评注此题常规解法相当繁琐,本解法由BC=2以静制动,突显了几何直观的优越性.

三、求面积的最值

例5在∆ABC中,三边长a,b,c满足a2+b2+2c2=8,则∆ABC的面积的最大值为______.

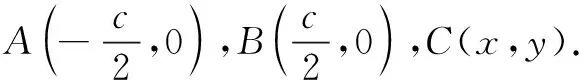
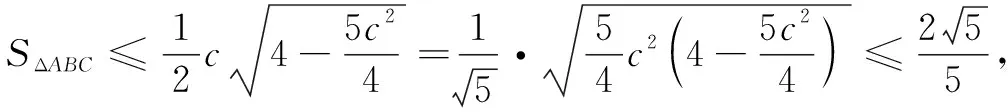
评注本题将AB固定,合理建立坐标系,从几何角度将代数问题坐标化,由点C的轨迹方程将面积转化为边c的函数,结合均值不等式求得面积最大值,降低了思维强度,实现高效解题.

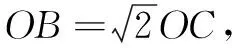
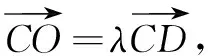
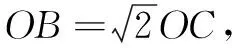
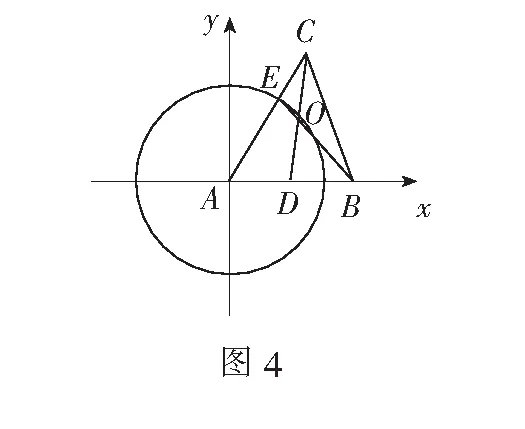
评注本题仍是利用阿氏圆解题,若借助其他解法,都不如轨迹法运算量少、简单直观.

四、求参数的最值

例7在∆ABC中,已知sinA+sinB+λsinAsinB=0,且a+b=2c,则实数λ的最大为______.

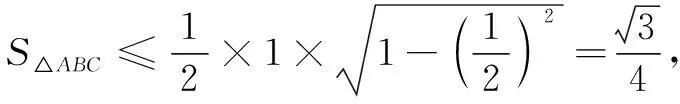
评注注意到题设条件刻画的是三角形的形状,可设定c边长度,借助轨迹思想巧妙地避开复杂的代数运算.通过正弦定理和面积公式将参数λ表示成椭圆焦点三角形面积的函数,从而快速得到参数的取值范围,起到四两拨千斤的效果.