电机驱动驻车系统的非线性自抗扰控制

姚 芳 ,姜 帆 ,吴正斌 ,李贵强 ,武利强

(1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室,天津 300132;2.天津中科先进技术研究院有限公司,天津 300392;3.中国科学院大学深圳先进技术研究院,广东深圳 518055;4.北京科瑞远腾测控技术有限公司,北京 100191)

1 引言

电子驻车是一种由电子控制方式实现停车制动的技术,是一种主动安全的刹车模式,美国TRW公司在原电子驻车制动系统(electrical park brake,EPB)基础上于2011年推出了改进型的EPBi,将控制部分与整车控制单元集成,驻车时根据接收到的各传感器信息,通过开关及控制器局域网总线数据(controller area network,CAN)总线数据控制电机,并经过传动系统作用于制动活塞,产生所需的制动力[1];Bosch公司于2010年量产一种将电机驱动与制动卡钳相结合的自动驻车制动系统(automatic parking brake-Maley brake,APB-M)系统,该系统用一根电缆交互数据,控制两个后轴制动卡钳上的电机,实现驻车制动[2];国内电子驻车制动的研究也越来越受到关注.文献[3]中,讨论了EPB系统实现汽车坡道起步自动控制的可行性,提出基于角度传感器的坡道阻力计算方法,设计了坡道起步过程中驱动力与驻车制动力的协调控制策略.文献[4]中,采用比例积分微分控制(proportional integral derivative,PID)方法解决坡道起步过程中的驻车制动力释放滞后问题.文献[5]中,建立坡道起步的受力模型,分析气压式EPB工作原理,采用Bang-Bang控制策略实现坡道起步的气压控制目标.文献[6]中,建立了坡道起步的EPB气压控制模型,提出用逻辑门限实现目标控制策略.从坡道驻车的相关研究成果可见,坡道驻车需依靠控制制动系统来实现.坡道和车辆载荷的变化引起未知坡道阻力的变化,给EPB制动力的精确调节带来很大困难.

为解决上述问题,本文提出使用驱动电机实现电动汽车驻车制动.磁场定向控制技术不断发展,能够实现电机转矩的快速精准控制,保证输出转矩与车辆行驶阻力矩的匹配,采用控制驱动电机实现电子驻车成为可能,但驱动电机实现电动汽车驻车制动,不仅需考虑驱动电机的高阶、强耦合特性,还需考虑整车质量、坡度等条件参数的不确定性.电机控制采用滑膜控制、模糊控制、神经网络及自适应控制算法,提高系统的动态性能和稳态精度[7],但无法解决响应快速性和超调性间的矛盾,难以应对未知扰动.

自抗扰控制(active disturbance rejection control,ADRC)是一种无需建立精确电机模型的新型控制算法,它继承了PID控制的优点,改进了其快速超调的缺点,有强抗扰性和鲁棒性[8].本文考虑坡道驻车过程中负载扰动和电机内部参数的动态变化,结合电机数学模型和车辆坡道纵向运动学模型,设计了电动汽车电子驻车过程永磁同步电机的自抗扰控制方案,搭建了电子驻车自抗扰电机控制器.相比PID控制,自抗扰控制可解决响应快速性和超调性间的矛盾,减少动态响应时间,并削弱因车辆不稳产生的抖振现象.

2 坡道电子驻车过程的非线性分析

2.1 永磁同步电机模型分析

永磁同步电机(permanent-magnet synchronous motor,PMSM)为高阶、非线性、强耦合的复杂系统,磁场定向控制通过Clark和Park变换对其进行解耦,将三相静止坐标系下电流ia,ib,ic变换成两相旋转坐标系下电流id,iq,简化了计算过程.以A轴为参考轴,PMSM等效物理模型如图1所示.

电子驻车过程持续时间短,对电机运行效率无要求,但对响应速度要求高,故采用最简单的id0控制策略,则定子电流矢量始终存在于q轴,d轴无分量.PMSM电磁转矩方程为

其中:pn为电机极对数;iq为定子电流q轴分量;λm代表永磁体磁链.

图1 PMSM等效物理模型Fig.1 Equivalent physical model of PMSM

PMSM运动方程为

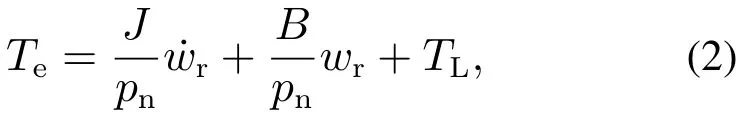
其中:TL为负载转矩,J为电机转动惯量,B为阻尼系数,wr为电角转速.

由式(1)–(2)可得

式(3)为以交轴电流iq为输入、电角度θr为输出的二阶系统(位置环),电角转速wr受到负载转矩TL、转动惯量J、定子电流iq等因素共同作用,要提高系统的响应性能,就需克服控制对象非线性因素及不确定扰动因素的影响.

2.2 坡道电子驻车过程动力学分析

设车辆沿斜坡方向为x轴,垂直斜坡方向为y轴,z轴垂直于x,y轴向外,车辆静止时绕z轴转动角度为θ.电动汽车坡道受力情况如图2所示.

图2 电动汽车坡道驻车受力分析Fig.2 Force analysis of electric vehicle when parking on slope

图2中: θ为道路坡道角(◦);G为车辆等效总重力,由车辆质量mv和车辆未知负载质量me引起,为

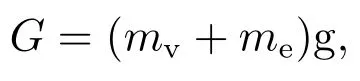
g为重力加速度(9.81 m/s2);FN为坡道对车辆的支持力,等于车辆等效总重力G在y轴分力G cos θ;Fg为坡道阻力,即车辆等效总重力G沿x轴分力G sin θ;Ff为滚动阻力,等于滚动阻力系数Ad与FN之积;Fk为空气阻力,为

其中: ρair为空气密度(kg/m2),A为车辆的迎风面积(m2),Cd为空气阻力系数.坡道阻力Fg驱动下车辆溜坡,同时产生加速阻力Fa,FaFg−Ff−Fk,若不采取制动措施车辆会出现极其危险的加速溜坡现象[9–10].传统车辆依靠制动卡钳摩擦力抵消车辆坡道阻力实现驻车功能,本文采用电机驱动驻车方式,通过调整电流iq间接调整电机输出电磁转矩Te和制动力Fb,制动力Fb与坡道阻力反向,实现车在坡道制动功能.

2.2.1 制动过程动力学分析

为抑制溜坡、控制后溜距离s最小,需施加与坡道阻力反向的车辆制动力Fb,动态补偿下滑加速阻力Fa,满足

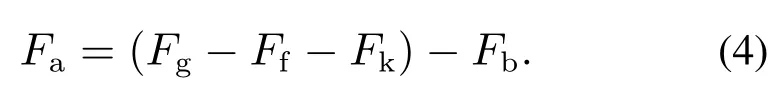
制动过程中Fb应大于Fg−Ff−Fk,使下滑加速阻力Fa为负值,直至车辆速度v稳定为0[11].制动过程车辆动力学方程为

其中:δ为旋转整车质量换算系数;r为车轮半径;ig为变速器传动比;i0为主减速器传动比;n为电机转速,与车辆速度比由式(4)–(6)可得

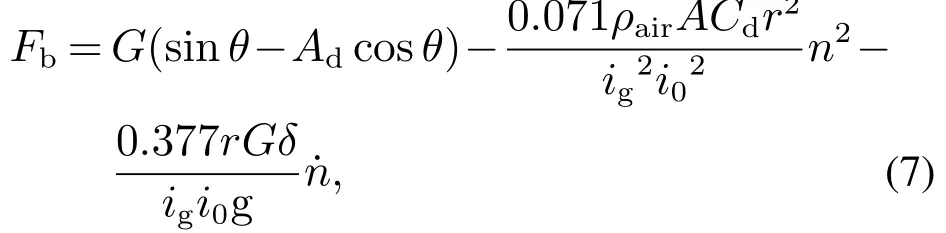
制动力Fb(iq,n)由电机提供,表达式为

其中η为传动效率.

由式(5)–(6)可见,制动过程是溜坡距离s的二阶系统;由式(7)–(8)可见,制动力Fb及电磁转矩Te是转速n的非线性函数,其中含n2的非线性项由空气阻力所致,一般很小;由式(7)可见,道路坡道角θ以三角函数形式约束坡道阻力和滚动阻力,对制动力Fb有非线性影响;此外,坡道起伏不平还会引起道路坡道角θ变化,形成外部扰动.因此,电子驻车制动过程是有外部扰动干预的溜坡距离s的二阶非线性系统.

车辆坡道停稳后,松开脚刹,车辆会在坡道阻力Fg驱动下产生溜坡现象,加速阻力Fa沿坡道向下;起初制动力Fb快速增大,克服坡道阻力Fg做功,加速阻力Fa沿坡道向上,车速开始下降;随后制动力Fb缓慢降低,加速阻力Fa逐渐减小为零,车速稳定回零静止.

电机转速n由0开始增大时车辆开始溜坡,当即刻起动电子驻车控制系统.转速n先增后减,直至为0.转速n一旦为0,驾驶员当即刻操控车辆进入机械制动或行车状态.

2.2.2 静止状态动力学分析

车辆驻车稳定后有FbFg−Ff−Fk.假设:1)不计空气阻力Fk和滚动阻力Ff;2)道路坡道角θ足够小,取sin θθ.在此假设下,制动力Fb与道路坡道角θ近似呈正比:

电子驻车过程中,电机内部损耗、逆变器等非线性因素为内扰,道路坡道角θ、车辆负载me等变化为外扰.当车辆未知负载me增大或道路坡道角θ变大,通过调整交轴电流目标值iqref间接调整Te和Fb,使电机电角度观测量θr和电角转速观测值wr经抖动后分别恢复到一稳定最小值和零值状态,完成静止状态抗扰动控制.

3 坡道电子驻车自抗扰控制器设计

自抗扰控制器由跟踪微分器(tracking differentiator,TD)、扩张状态观测器(extended state observer,ESO)和非线性状态误差反馈控制律(nonlinear states error feed-back,NLSEF)配合反馈控制组成,可估计影响系统输出的扰动,并主动进行直接的扰动抑制,满足驻车系统控制要求.考虑坡道电子驻车过程的特点,本文采用位置–电流双闭环控制,内环采用一阶线性ADRC 电流环,外环采用二阶非线性ADRC位置环[12].

3.1 位置环二阶非线性自抗扰控制器设计

根据式(3),以电角度观测值θr、电角度目标值θref和交轴电流目标值iqref为状态量、输入量和输出量,设计非线性自抗扰控制器(nonlinear active disturbance rejection control,NADRC).其中:为综合了外扰和内扰的系统总扰动Neso,是有界的;为系统控制量增益b.根据动力学分析,坡道电子驻车NADRC的控制目标为电角度观测值θr尽可能小及电角速度wr为零.

3.1.1 电角度跟踪微分器设计

为减小电角度目标值θref大幅度变化导致的超调,设计跟踪微分方程:

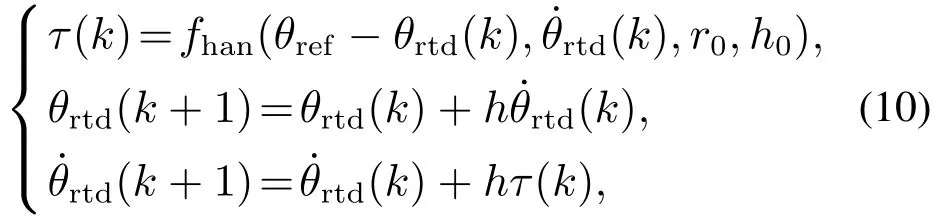
其中:电角度跟踪值θrtd为TD的输出,τ为最速综合指数(过度函数),k为跟踪步序号,h为积分步长,最速综合函数fhan(x1,x2,r0,h0)[8]为

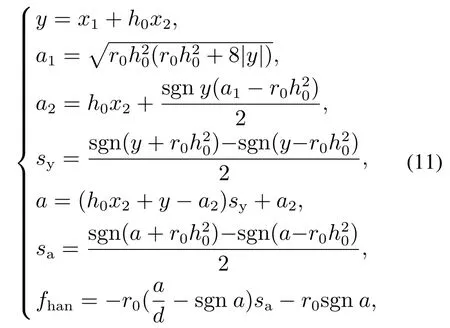
其中: h0为滤波因子,r0为速度因子.该过程实现了θrtd快速无超调的跟踪电角度目标值θref,并输出其微分信号

3.1.2 电角度扩张状态观测器设计

ESO以电角度观测值θr和交轴电流目标值iqref的扩张值b0iqref为输入,估计系统总扰动Neso和ESO的输出θreso:

其中:ε1为误差信号;θreso为ESO输出跟踪值;Neso为估计出的未知扰动;β01,β02和β03为控制参数;fal为非线性最优综合控制函数:

其中:δ为线性段区间长度[8];Neso表征车辆道路坡道角θ及负载质量me等未知变化引起的综合扰动.

3.1.3 电角度非线性误差反馈控制设计

NLSEF对TD及ESO输出的电角度差值e1和电角速度差值e2按最速综合函数进行二阶非线性组合、设计控制量u0,NLSEF方程为

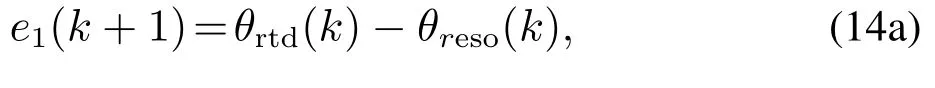
总扰动Neso以交轴电流目标值iqref为补偿控制量对u0进行线性补偿,扰动补偿方程为

其中b0为补偿因子,尽可能整定为b值.

3.1.4 坡道电子驻车二阶NADRC方案设计

考虑系统内部扰动、外部扰动、模型不确定性等因素影响,设计外环位置环的二阶非线性自抗扰控制器—NADRC,结构如图3所示.

图3 位置环二阶NADRC控制结构Fig.3 Second-order nonlinear ADRC structure of the position loop

3.2 电流环一阶线性自抗扰控制设计

驻车控制中,当车辆未知负载me或道路坡道角θ变化,如果电流环不能及时调节电磁转矩Te,车速将无法快速回零,对系统控制性能产生很大影响.采用id0的磁场定向矢量电机控制技术,得出d–q轴电流状态方程为

根据式(16),以交直轴电流观测值id,q、交直轴电流目标值id,qref和交直轴电压目标值ud,qref为状态量、输入量和输出量,设计线性自抗扰控制器(linear active disturbance rejection control,LADRC),如图4所示.

在图4 中,wc为比例器的带宽,限幅器的幅值为[−400 V,400 V],ieso为线性观测器(linear extended state observer,LESO)的电流估计值,状态矩阵A、输入矩阵B和跟踪矩阵C设计为[8]

其中w0为观测器带宽.

图4 电流环一阶LADRC控制结构Fig.4 First-order linear ADRC structure of current loop

电流环一阶LADRC可等效为PD控制,其输出交直轴电压目标值ud,qref经逆变器控制交直轴电流观测值id,q,同时作为LESO的输入.交直轴电流观测值的扰动为LESO输出id,qeso的导数,用于扰动的实时补偿.适当选取控制参数w0,wc及采样周期h,整定参数减少,调试方便,提高控制准确度.

4 电子驻车自抗扰仿真及试验验证

本文搭建了PMSM自抗扰控制的Simulink仿真模型和实车试验系统,对比所设计的PMSM自抗扰控制器和PID控制器在电子驻车过程的应用效果.仿真和试验涉及的车辆参数包括:车身质量为800 kg,车轮型号为145/70R12,车轮主减速器传动比为10,最大载重200 kg.

4.1 PMSM自抗扰仿真研究

4.1.1 电子驻车自抗扰仿真设计

电子驻车的PMSM自抗扰控制仿真模型如图5虚框所示.

PMSM仿真参数如下:额定相电压Un220 V,额定相电流In5.01 A,额定功率PN3 kW,额定转速n3000 r/min,额定频率fn150 Hz,交轴电感Lq2.65E−2 mH,直轴电感Ld1.4E−2 mH,定子电阻R1.8622 Ω,永磁体磁链为λm0.330 V·s,极对数pn3;转动惯量为J0.003 kg·cm2,阻尼系数为B0.095 N·m·s,驻车坡度θ5◦,为车辆负载添加平均值为0、方差为2及采样时间为0.1 ms的随机扰动信号;算得电机负载转矩TL∈(68 N·m,85 N·m).据此考虑负载转矩取TL(68 N·m,75 N·m,80 N·m,85 N·m),设计电子驻车自抗扰正交仿真方案,如表1所示.

表1 电子驻车自抗扰正交仿真方案Table 1 Orthogonal simulation scheme of PMSM with the auto disturbance rejection control in the process of electronic parking

图5 PMSM自抗扰控制仿真模型Fig.5 Simulation model of PMSM with the active disturbance rejection control

4.1.2 电子驻车过程仿真结果及其分析

电子驻车过程电机定子三相电流和电磁转矩、转速及后溜距离分别如图6–9所示.

由图6可见,相比PID控制,ADRC下电子驻车过程电机定子三相电流暂态持续时间短.电机定子三相电流主要为自适应调节的q轴电流分量,产生电子驻车过程动态的电磁转矩Te及制动力Fb,直至驻车达到静止状态.此时,定转子相对位置不变,定子三相电流ia,ib,ic恒定,提供补偿坡道阻力Fg的电磁制动力Fb.

图6 68 N·m负载下电子驻车过程电机三相定子电流Fig.6 3–P stator current of PMSM in the process of electronic parking process under 68 N·m load

由图7可见,ADRC方式下,电磁转矩Te波形振动大,反应快速,则车辆制动力Fb变化快速,实时抵消车辆随机扰动引起的车速变化能力强.

图7 不同仿真方案时电子驻车过程电磁转矩Fig.7 Electromagnetic torque during electronic parking process under different simulation schemes

由图8不同负载下电子驻车过程转速可见,相比PID控制,ADRC控制下电机转速超调明显降低,车辆后溜最大转速减少,车辆扰动引起的车速变化能被快速抵消,振荡得到有效抑制,且响应速度加快,提高了驻车控制性能.

由图9可见,相比PID控制,相同负载下ADRC控制时车辆的后溜最大距离smax短,且接近稳定时车辆震荡小,平衡性能好.

图6–9的仿真结果均表明,ADRC控制比PID控制响应速度更快、平稳性更优及后溜距离更小,更能满足车辆坡道驻车要求.

图8 不同仿真方案时电子驻车过程转速Fig.8 Motor speed during electronic parking process under different simulation schemes

图9 不同仿真方案时电子驻车后溜距离Fig.9 Slip distance during electronic parking process under different simulation schemes

4.1.3 ADRC与PID抗扰效果对比分析

根据电机转速及后溜距离仿真波形,取电机转速小于4 r/min为稳定状态,总结出转速曲线性状参数、车辆最大后溜距离如表2所示.

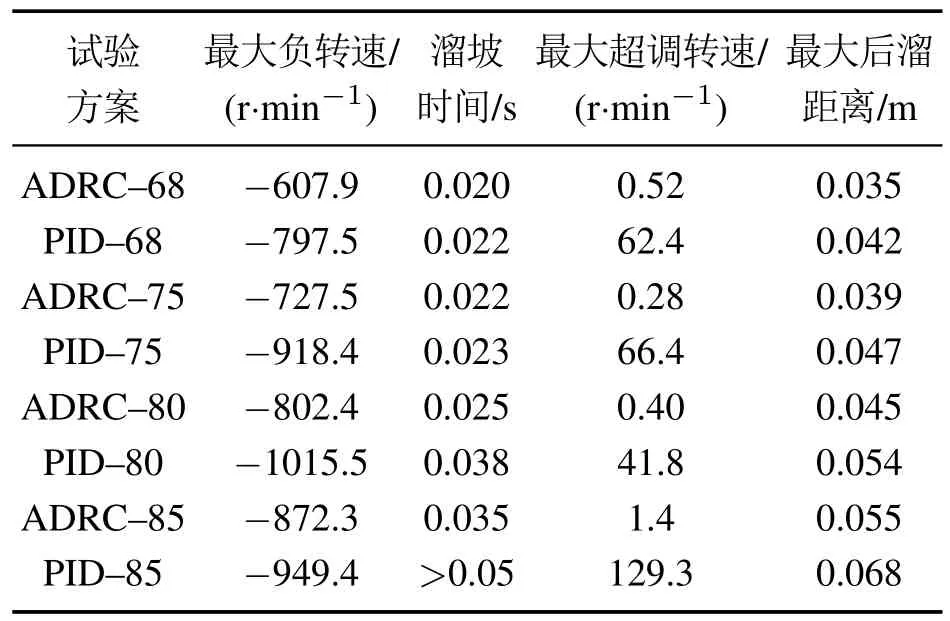
表2 不同仿真方案时电子驻车过程的最大负转速、溜坡时间、最大超调转速和最大后溜距离Table 2 Maximum negative vehicle speed,slip time,maximum overshoot speed and maximum slip distance during electronic parking process under different simulation schemes

由表2可见,ADRC控制方式下最大负转速为PID控制下的76%∼91%;溜坡时间为PID控制下的66%∼95%;ADRC最大超调转速近似为0,而PID控制下有较高的转速超调值;ADRC算法下最大后溜距离为PID控制下的82%∼83%.

4.1.4 PID和ADRC参数整定过程

1)PID控制器设计和参数整定.

根据电机系统的标称模型确定PID参数:

2)ADRC参数整定.

本文的ADRC 控制器采用了非线性组合函数fhan(),r0,h0,β01,β02,β03,h,b0,r1,h1和c为控制器参数.其中: r0由过渡过程快慢和系统承受能力决定;β01,β02和β03由系统采样周期决定;可简化处理让h0与h一致.系统真正需整定的参数为补偿因子b0、控制量增益r1、阻尼系数h1和精度因子c,一般r1大到一定程度即可,b0根据控制对象中b大小进行设置,越接近b越好.本文整定顺序为TD→ESO →NLSEF,首先让θrtd快速无超调的跟踪输入信号θref并输出其微分信号˙θrtd,再通过ESO输出θreso和˙θreso与输入的一致性进行参数整定,再经过小幅度微调得到理想控制效果.ADRC控制器参数{b0,h1,r1,c}的最优整定值为{1,0.5,2.5,20}.

4.1.5 驻车效果对比

定义车辆单位负载后溜距离为后溜距离值比输出转矩负载值,如表3所示.

表3 单位负载转矩后溜距离Table 3 Slip distance after unit load torque

由表3可见,相比PID控制,相同负载下ADRC控制时单位负载后溜距离明显更小;随着负载增大ADRC控制时单位负载后溜距离增量的增势更弱.

综上仿真分析,ADRC控制比PID控制,在系统稳定性、响应速度和后溜距离方面全面显著提升,电子驻车过程的抗扰性能优势显著.

4.2 基于自抗扰算法的电子驻车实车试验研究

4.2.1 电子驻车实车验证试验设计

将自抗扰控制器安装于低速电动试验车辆,前后轮距1.5 m,路面坡道角θ为10◦,前轮轴线初始位置1,2,3间距均为0.4 m,前轮轴线初始位置3距离平整路面与坡道交界点1 m,初始位置如图10所示.

图10 试验车辆及前轮3个轴线初始位置Fig.10 Experiment vehicle and 3 initial positions of its front wheel axis

试验车辆前后轮轴心分别在坡道和平整路面上时,车身倾角不等于坡道角,可模拟负载扰动.为对比ADRC和PID控制的抗扰效果,设计电子驻车实车试验方案,如表4所示.

表4 电子驻车实车试验方案Table 4 Design of electronic parking orthogonal simulation scheme

试验方案ADRC–I和PID–I,电子驻车过程前轮轴心初始于位置1,后溜过程中前后轮均在坡道上,车身倾角等于坡道角、等值负载转矩基本不变.试验方案ADRC–II和PID–II,电子驻车过程前轮轴心初始于位置2,后溜过程中前轮保持在坡道上、后轮由坡道溜至平整路面,车身倾角变小、等值负载转矩减小.试验方案ADRC–III 和PID–III,电子驻车过程前轮轴心初始于位置3,后溜过程中前轮保持在坡道上、后轮保持在平整路面上、远离交界点,车身倾角变小、等值负载转矩减小.

实验中,电机控制系统的主控芯片采用TI公司的TMS320F28069.系统中,交轴电流环和直轴电流环采用相同的参数.参数整定后,各参数如下:PI电流环{Kp,Ki}的最优整定值为{16000,3200},PID位置环{Kp,Ki,Kd}的最优整定值为{2100,12000,20}.ADRC电流环{h,b0,w0,wc}的最优整定值为{1000,12,35,85},ADRC位置环{r0,β01,β02,β03,b0,c}的最优整定值为{25,1000,10000,500,35,50}.

4.2.2 电子驻车实车验证试验结果及分析

图11–12分别为3种ADRC试验方案和3种PID试验方案时电子驻车过程的车速;图13为ADRC与PID共6种试验方案时电子驻车过程的车辆后溜距离;表5列出6种试验方案时电子驻车过程的负转速最大值、溜坡时间和后溜最大距离.

由图11–13及表5可见,车身倾角引起的外部扰动对车辆后溜距离有影响,ADRC控制下负转速最大值、溜坡时间和最大后溜距离分别为PID控制下的79%∼89%,89%∼100%和83%∼84%.

综上试验结果分析,ADRC控制比PID控制,在响应速度和后溜距离方面全面显著提升,电子驻车过程的抗扰性能优势显著.

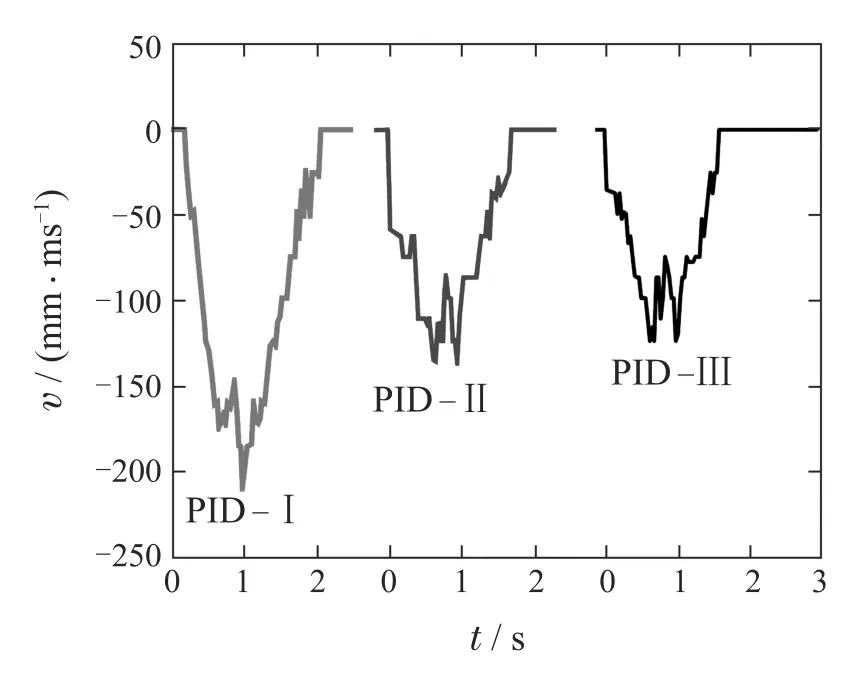
图12 3种PID实车试验方案时电子驻车过程车速Fig.12 Vehicle speed during electronic parking process under 3 PID vehicle experiment schemes

图13 不同实车试验方案时电子驻车后溜距离Fig.13 Slip distance during electronic parking process under diferent vehicle experiment schemes

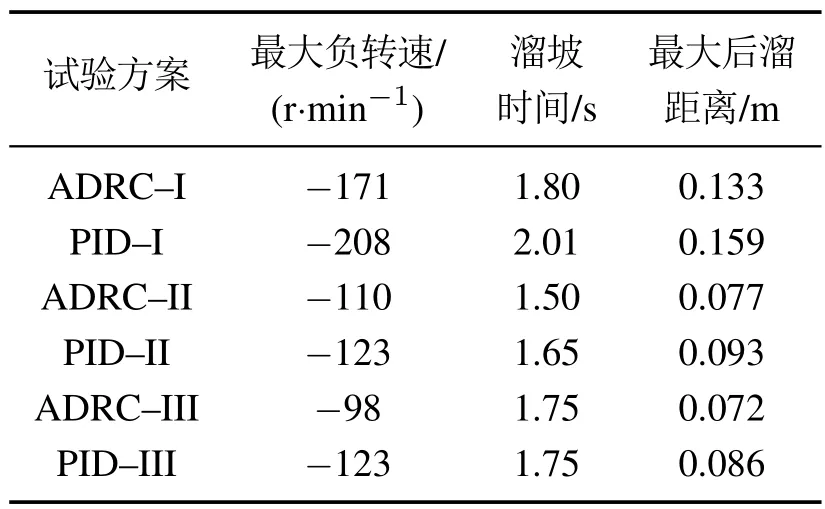
表5 不同试验方案时电子驻车过程的负转速最大值、溜坡时间和最大后溜距离Table 5 Maximum negative vehicle speed,slip time and maximum slip distance during electronic during electronic parking process under different vehicle experiment schemes

5 结语

本文针对坡道电子驻车过程车辆的非线性动力特征和非线性扰动复杂的特点,以及PID 控制用于PMSM调速时“速度调节”和“超调量抑制”之间不可协调的矛盾,将自抗扰控制技术植入到坡道电子驻车过程的PMSM控制策略,主要成果与结论包括:

1)分析PMSM 数学模型,确定了一阶电流内环、二阶位置外环的PMSM控制策略;对车辆坡道电子驻车的制动过程和静止状态进行非线性动力学及扰动分析,将自抗扰控制技术融于电机控制策略,完成了二阶位置环NADRC和一阶电流环LADRC的设计,形成基于自抗扰控制的坡道电子驻车PMSM 控制策略进行非线抗扰控制.

2)仿真对比研究了ADRC和PID控制下坡道电子驻车过程的转速性状参数和车辆最大后溜距离,实车试验对比研究了ADRC和PID控制下坡道电子驻车的负转速最大值、溜坡时间和最大后溜距离.结果均表明采用ADRC技术的坡道电子驻车比采用PID技术的性能更优.表现为最大超调转速和最大负转速均更低,抖振得以抑制,说明驻车过程稳定性更优;溜坡时间和后溜距离均更短,说明驻车更快、后溜得到更有效抑制;单位负载转矩的最大后溜距离更小,说明基于ADRC控制的电子驻车制动效率更高.