非完整轮式机器人的鲁棒同步编队跟踪及镇定控制
周竞烨,李家旺,邸 青,方 凯,姚佳琪,黄汉涛
(宁波大学海运学院,浙江宁波 315211)
1 引言
近年来,非完整轮式移动机器人(nonholonomic wheeled mobile robot,NWMR)编队控制在相关领域受到了越来越多的关注,并在安全救援、侦察任务、矿物勘探、巡逻防卫等方面得到了广泛的应用.目前,NWMR的编队控制方法主要有领航–跟随法[1–4]、虚拟结构法[5–6]、基于行为法[7–8]等.
由于NWMR是一种典型的非完整系统,其编队控制问题一般会分为独立的两类子问题:编队跟踪和编队镇定.在编队跟踪问题中,要求编队的期望轨迹满足持续激励条件,即期望速度或角速度应不恒等于零.如文献[9]设计了一种自适应神经网络控制器以实现NWMR的编队跟踪控制方法.文献[10]中提出了一种级联跟随法,可实现直线编队控制.文献[11]针对含有未知信息的NWMR编队跟踪控制问题,提出了一种确定学习控制方法以改善控制性能.文献[12–13]利用反步法实现了移动机器人编队的精确跟踪控制.文献[14]通过引入激励函数形式实现了非完整系统的编队跟踪控制.针对编队镇定问题,文献[15]设计了一种光滑时变分布式控制以实现欠驱动船舶的编队镇定控制.文献[16]通过引入一种δ-持续激励函数,实现了多机器人的渐近编队镇定.
然而,在实际的NWMR编队作业任务中,期望轨迹往往具有一定的复杂性,即可能包含时变轨迹和固定点等.此时,采用单一的编队跟踪或编队镇定方法均无法实现整体控制目标,而通过多个控制方法进行切换则可能导致控制系统不稳定或失效.因此,设计出一种具有统一结构形式的NWMR编队控制策略,以实现同步跟踪和镇定,对于NWMR编队的具体应用具有重要的意义.目前,就笔者所知,尚无有关同步实现非完整系统编队跟踪和编队镇定的研究成果的报道,相关研究仅针对单个非完整系统.如文献[17]对单个NWMR设计了一种饱和动力学控制器以实现同步跟踪和镇定控制,但其对于初始状态较为敏感.文献[18]和文献[19]设计了一种饱和输入下的运动状态转化策略,也同步实现了对轨迹的精确跟踪和固定点的镇定,但控制器形式较为复杂.文献[20]针对速度受限的NWMR提出了一种跟踪和镇定统一运动学控制器,忽略了动力学影响.但需要指出的是,上述研究成果直接应用至非完整系统的编队控制问题上无法保证其控制性能.
基于上述分析,本文针对NWMR编队的同步跟踪和镇定控制问题进行了理论和仿真研究.考虑到实际情况,本文在NWMR数学模型中加入模型参数不确定性和输入饱和限制的影响.基于领航–跟随编队策略,定义了NWMR的编队结构数学表达形式,并确定了每个跟随者的期望轨迹;考虑到NWMR的非完整约束所引起的控制困难[21–22],为了实现跟随者对复杂期望轨迹的跟踪,定义了一种含辅助控制量的跟踪误差表达式,并设计了具有统一结构形式的运动学控制器.针对参数不确定性和输入饱和限制,基于模糊控制理论,设计了一种NWMR的饱和动力学控制器,使得跟踪误差能够收敛至零点附近的小邻域内,同时具有较好的抗饱和性和鲁棒性.最后通过仿真实验对所提出的控制方法的性能进行了验证.
2 问题描述
2.1 NWMR模型
考虑多个相同的NWMR组成的系统.单个NWMR结构如图1所示.图中:r为主动轮半径,b为NWMR主体半宽,d为NWMR质心Pc到主动轮中心P0的距离,(x,y)和φ分别表示NWMR的质心位置和首向角.第i个NWMR的运动模型可以描述为[17]

其中: ηi[xiyiφi]T,ω[ω1ω2]T为主动轮角速度;τdi∈R2为外界干扰项;G(τi)[g(τ1i)g(τ2i)]T为主动轮的有界控制转矩,其定义如下:

式中: τM>0是主动轮转矩的饱和值,sgn(·)为标准符号函数.

图1 非完整轮式机器人Fig.1 Nonholonomic wheeled mobile robot
此外,矩阵R(φi),M,C和D定义如下:

其中:

mc和mw分别表示NWMR主体和主动轮的质量,Ic表示NWMR主体绕质心的转动惯量,Iw和Im分别表示主动轮绕其中心轴和垂直轴的转动惯量,djji>0(j1,2)表示阻尼系数.
为了便于后续研究,现对式(1)作适当处理.定义νiEωi,其中: νi[uiwi]T,ui表示线速度,wi表示角速度,此时,式(1)可表示为


根据实际情况,令NWMR满足以下假设.
假设1外界干扰有界,即存在正常数使得,j1,2.
2.2 编队模型
本文采用领航–跟随编队控制策略[23–26],其结构如图2所示.

图2 领航–跟随编队结构示意图Fig.2 Leader-follower formation structure
图中,领航者的运动轨迹(xa,ya,φa)假设为已知的,第i个跟随者的期望运动轨迹(xdi,ydi,φdi)由下式定义:

式中:Li和δdi分别表示领航者与第i个跟随者之间的期望相对距离和期望相对角度;ζi表示第i个跟随者的非完整约束补偿角,其定义为

其中ua和wa分别表示领航者的线速度和角速度,且满足以下方程:

式中各物理量定义与式(3)中第1个方程类似.同理,式(4)也可等价地表示为以下微分方程:

对于期望轨迹,给出以下假设.
假设2所有跟随者的期望速度νdi及其导数都是有界的.
2.3 控制目标
本文的控制目标:考虑由式(3)表示的多个NWMR组成的编队系统,在领航者运动状态已知的条件下,针对每个跟随者,通过设计饱和控制输入使其运动轨迹(xi,yi,φi)能够跟踪上期望轨迹(xdi,ydi,φdi),并保证跟踪误差(xi−xdi,yi−ydi,φi−φdi)收敛至零点附近的有界邻域内.不失一般性,期望轨迹(xdi,ydi,φdi)可以是满足假设2的任意轨迹,包括时变轨迹或固定点等.
3 控制器设计
3.1 运动学控制器设计
为了解决由于NWMR的非完整约束所引起的欠驱动问题,首先定义新的跟踪误差表达式为

式中:

βxi和βφi为辅助控制量,其表达式后续确定.
将式(8)对时间求导,可得跟踪误差方程为


根据假设2和三角函数关系不难得知,ϖxi和ϖyi有界且满足
为了镇定跟踪误差xei和φei,将ui和wi视作虚拟控制输入,并定义为

式中uvi和wvi分别表示ui和wi的虚拟控制输入量.将式(10)代入式(9),可得
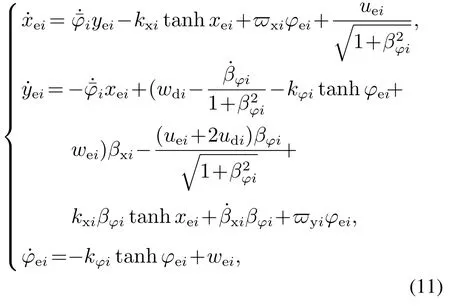
式中ueiui−uvi和weiwi−wvi表示虚拟控制误差.
为了镇定跟踪误差yei,将辅助控制变量βxi和βφi视为虚拟控制输入.考虑到期望轨迹的复杂性,首先令βxi和βφi的表达式为

式中:βxi,1,βφi,1和βφi,2为待确定的辅助控制分量;

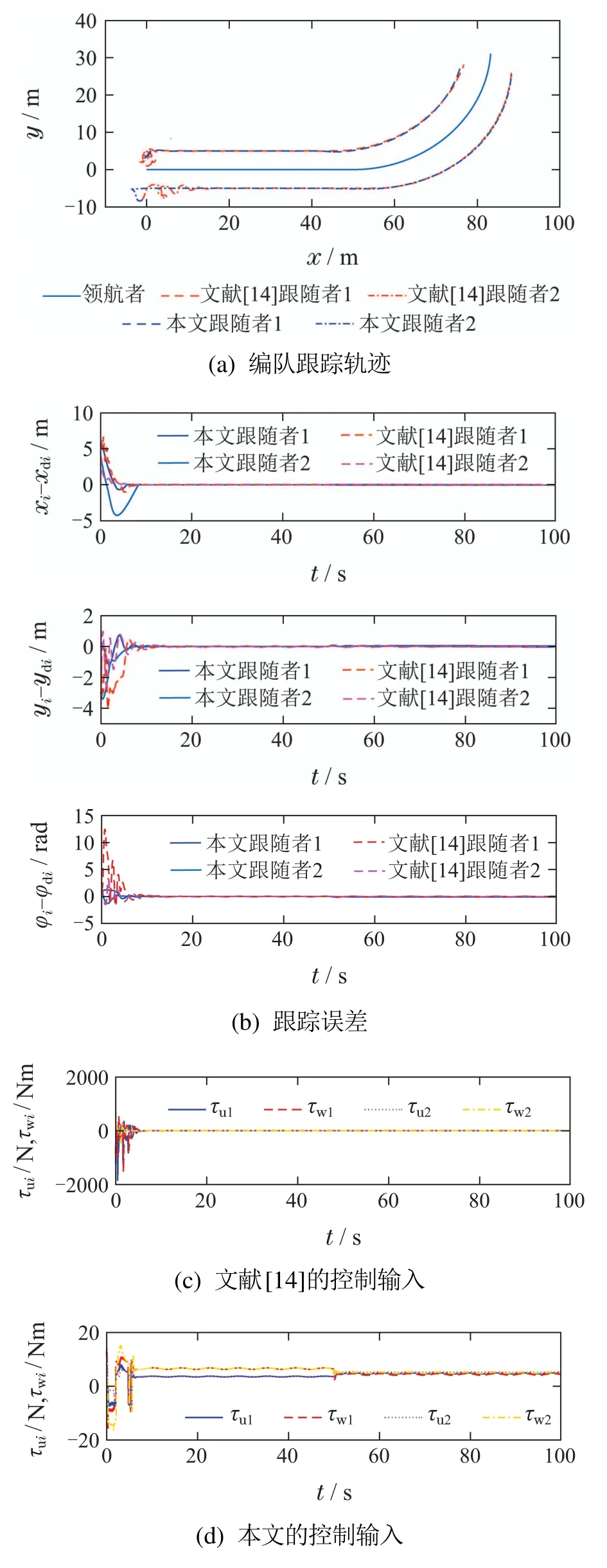
u0为一个较小的正常数;1−F(udi).不难得知,当|udi|u0时,F(udi)≈1;当|udi| 对式(12)求导可得 为了确定式(12)中βxi,1,βφi,1和βφi,2的具体形式,首先对期望速度udi不同取值情况下的式(11)中表达式进行分析: 1)当|udi|u0时, F(udi)1, βxi0, βφiβφi,2.此时,表达式可简化为 2)当|udi| 根据上述分析,为了镇定跟踪误差yei,选择βxi,1,βφi,1和βφi,2为 式中: kyi和kΩi为正常数,Ωi且Ωi(0)>0,ΩieΩi−Ω0,Ω0为一个小的正常数, 为了镇定虚拟控制误差uei和wei,本节将对饱和控制输入进行设计.首先,结合式(3)和式(10)可得误差动力学分量形式为 考虑到上式中Fji(j1,2)包含未知建模信息,且和的形式较为复杂,为了简化控制设计,本文采用模糊系统对上式中的Fji−进行近似.该模糊系统由以下模糊If–Then规则组成[27–28]: If z1isand ··· and znis,then W is Bi,i1,2,···,N, 其中:zj(j1,2,···,n)∈Rn和W ∈R分别为模糊系统的输入和输出,是隶属函数,Bi是输出的模糊集.此时,模糊系统的输出可表示为 对于任意有界连续函数Y(z),根据模糊系统特性,存在最优逼近常量θ∗满足 结合上述特性,式(19)可表示为 其中:zui[uiwi,zwi[uiwi表示模糊系统的输入信号,εui和εwi表示模糊估计误差. 根据式(20),设计控制输入为 其中γji和δji(ju,w)均为正常数. 此外,考虑到|ξi|1,则结合式(22)不难得到,式(21)满足以下不等式: 则所设计的控制输入式(21)将不会违反饱和限制条件式(2).此时,将式(21)代入式(20),并定义参数估计误差,ju,w,结合式(22),整理后可得误差动力学方程为 定理1考虑由式(11)(18)(25)组成的误差系统.当假设1和假设2成立时,通过选取合适的控制参数kxi,kyi,kφi,γui和γwi,并保证不等式(24)成立,则所有误差信号xei,yei,φei,uei,wei,均全局收敛至零点附近的有界小邻域内. 证为了简化证明,根据跟随者的期望轨迹的差异,对上述误差系统分为以下两种情况进行考虑. 1)|udi|u0:此时,式(18)中第1个表达式成立选择以下备选Lyapunov函数: 其中λji(j1,2,3)为合适的正常数.对式(26)求导,结合式(11)(25)(18)中第1个表达式,可得 其中λxyi,λxui,λxφi,λyφi,λyui,λφwi,λuεi,λwεi,λufi,λwfi,λθui,λθwi为合适的正常数以使得>0(ju,w)和>0(jx,y,φ,u,w). 考虑到−xeitanh xei−tanh2xei,|εji|,ju,w,可以为任意小正常数,并结合假设1式(28)可简化表示为 式中: 2)|udi| 通过与情况1中分析类似过程,可得 式中:K2和C2为合适的正常数.因此,所有误差信号xei,yei,φei,uei,wei,均全局收敛至零点附近半径满足∥X∥的有界小邻域内. 综上,可以得出结论:所有误差信号xei,yei,φei,uei,wei,均全局收敛至零点附近的有界小邻域内.证毕. 根据上述结果,下面给出本文的主要结论. 定理2考虑多个NWMR组成的编队系统(1)或系统(3)并认为假设1–2成立.当领航者运动状态已知时,针对每个跟随者,在饱和控制输入(21)作用下,通过选取合适的控制参数kxi,kyi,kφi,γui和γwi,并保证不等式(24)成立,则其跟踪误差ηi−ηdi能够全局收敛至原点附近的有界小邻域内. 证根据定理1 结论和式(8)可知,为证明跟踪误差ηi−ηdi全局收敛,仅需证明βxi和βφi的有界性即可.为此,通过对式(12)分析可知 对于βφi,2,由式(17)中第2个方程可知 对于βxi,1和βφi,1,根据式(17)中第1个方程,取备选Lyapunov函数 并求导可得 则当Ωi>Ω0时,<0,即βxi,1和βφi,1是全局收敛的.因此,结合Ωi定义,可知 结合式(34)–(35)(37)可知,βxi和βφi是有界的,再由定理1,可得出结论:跟踪误差ηi−ηdi能够全局收敛至原点附近的有界小邻域内.证毕. 为了验证文中所设计的控制方法的性能,本节对由多个NWMR组成的编队控制问题进行了仿真试验.NWMR的模型参数为[14] 干扰项:τd1i0.05 sin(0.1t),τd2i0.05 sin(0.1t). 首先,对NWMR编队跟踪控制问题进行了仿真研究.该编队由领航者和2个跟随者组成,领航者与跟随者之间的期望距离和相对角度分别为 仿真前50 s,领航者的线速度和角速度为 之后设定为 控制参数设定为 模糊系统中输入变量zui和zwi的模糊集个数为3个,总的模糊规格为27个.选择高斯函数隶属函数,其中高斯函数的中心为(−3,0,3),宽度为3.仿真结果如图3所示. 由图3可以看出,在本文控制器作用下,跟随者的跟踪误差均收敛至零点附近的有界小区域内,且控制输入均未超出其饱和限制值.此外,作为对比,上图中还给出了采用文献[14]中控制方法的仿真结果.不难发现,与本文方法相比,文献[14]中方法可以得到类似的稳态跟踪精度,但其在仿真初期会引起跟踪误差较为剧烈的振荡,并引发对控制输入远超其饱和限制值的需求. 图3 编队跟踪仿真对比Fig.3 Formation tracking simulation comparisons 为了验证本文控制方法在编队镇定问题上的有效性,本节针对由1个领航者和4个跟随者构成的编队镇定控制问题进行了仿真.其中,领航者的轨迹设定为ηa[0 0 0]T,其与第i个跟随者之间的期望距离和相对角度设为Li,δdi(2i −1)π/4.控制参数设定与上述跟踪控制问题中相同. 结果如图4所示. 图4 编队镇定仿真对比Fig.4 Formation stabilization simulation comparisons 作为对比,图4中也给出了采用文献[15]中控制方法的结果.不难看出,与文献[15]中控制方法相比,本文控制方法在输入饱和限制条件下具有较小的稳态跟踪误差.不仅如此,如图4(b)所示,本文控制方法能够确保角度跟踪误差收敛至零点附近的小邻域内,而文献[15]中控制方法无法做到. 此外,为了进一步验证本文控制器的抗饱和性和鲁棒性,本节对较大初始位置误差和存在状态突变情况下的NWMR编队跟踪控制问题进行了仿真研究.编队结构与前述跟踪情况相同.仿真前100 s内,领航者的线速度和角速度分别为ua2 m/s,wa0 rad/s,之后为ua2 m/s和wa0.05 rad/s,且在t100 s时,其中领航者的期望状态从(200,0,0)突变为(170,30,0).另外,跟随者的初始状态分别设定为 控制参数设定与前述相同.仿真结果如图5所示. 由图5可以看出,在存在较大初始误差和状态突变情况下,本文控制方法依然保持了良好的控制性能,且控制输入始终保持在饱和限制范围内,具有优良的抗饱和性和鲁棒性. 图5 大初始误差和存在位置突变的编队跟踪仿真Fig.5 Formation tracking simulation with large initial errors and ideal position change 本文针对带有参数不确定性和控制输入饱和限制的NWMR编队的同步跟踪和镇定控制问题进行了仿真研究.利用领航者跟随者编队策略,通过设置领航者和跟随者的相对距离和夹角,给出跟随者的期望轨迹,对于单个跟随者,通过在跟踪误差模型中引入辅助控制量,设计出具有统一结构形式的运动学控制器以实现对不同类型期望轨迹的跟踪,包括时变轨迹和固定点等.针对NWMR的模型不确定性和输入饱和限制,采用模糊控制方法,并结合反步法,设计出一种饱和动力学控制器,可以使得跟踪误差全局收敛至零点附近的小邻域内,且控制输入不会超出饱和限制值.仿真试验证明,本文方法可以实现NWMR编队的同步跟踪和镇定控制,并对大初始误差和状态突变等情况具有良好的鲁棒性.尽管如此,本文控制方法的相关性能还有待通过实际的NWMR编队实验做进一步的验证,这也是作者后续工作的重点开展方向.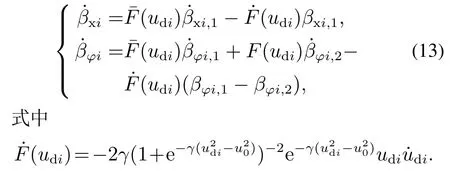






3.2 动力学控制器设计

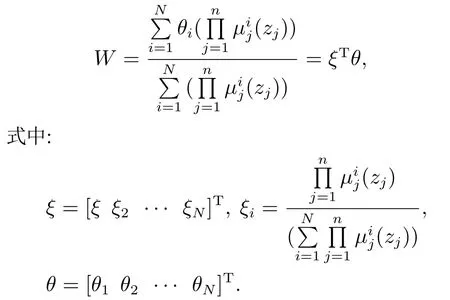
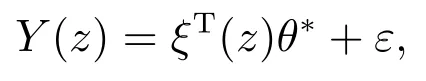


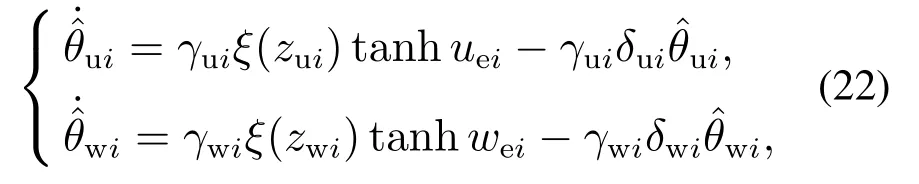



4 稳定性分析



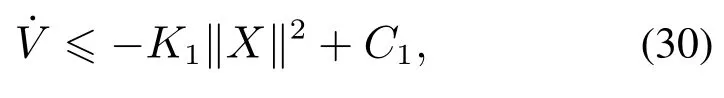
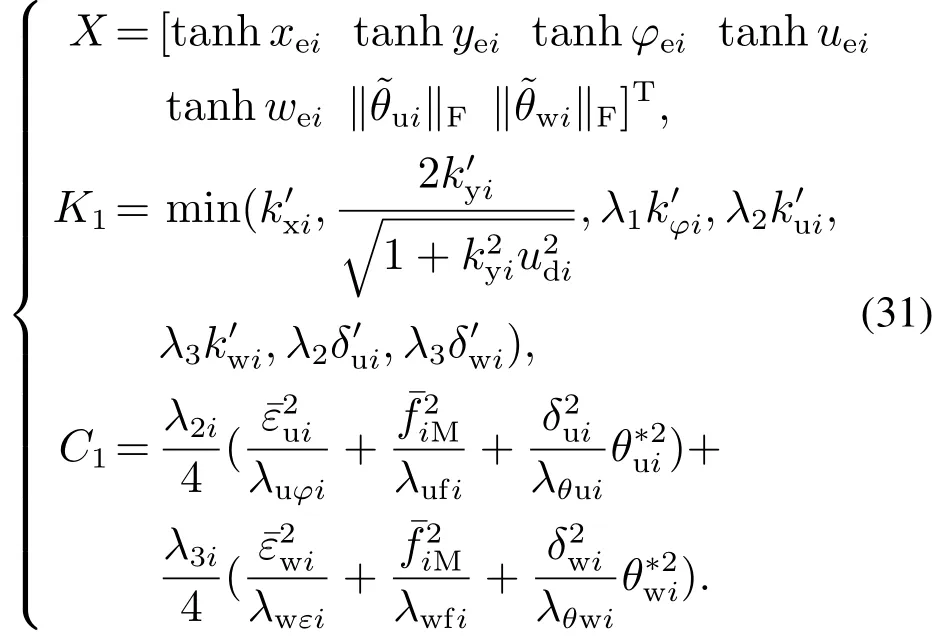


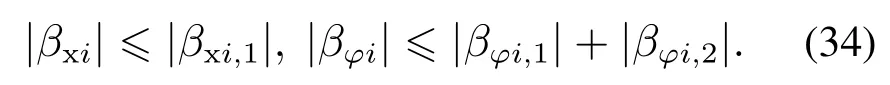

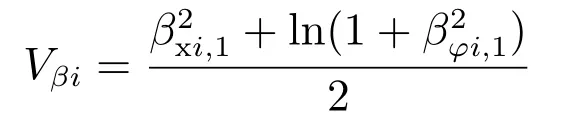
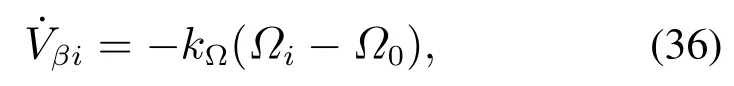

5 仿真试验




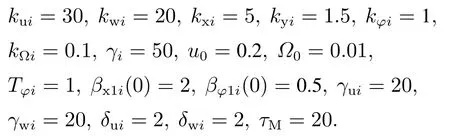






6 结论
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

