改进的迭代收缩阈值算法及其在量子状态估计中的应用

丛 爽,丁 娇,张 坤

(中国科学技术大学自动化系,安徽合肥 230027)

1 引言

量子层析(quantum tomography)是最常用的量子状态估计方法,最早由Stokes于1851年提出[1].量子层析是对量子状态的大量全同副本进行多次测量,作为量子状态在某个方向上的投影(坍缩)的概率,通过对所获的概率进行逆变换,反解出量子状态的密度矩阵[2].量子层析在包括量子计算机应用在内的量子态制备,以及量子系统控制中的状态反馈控制都具有重要意义.一个n比特量子系统可用密度矩阵ρ ∈Cd×d(d2n)描述其状态,并且密度矩阵需满足半正定、单位迹的厄米矩阵约束.该系统的完备测量次数为d2,它是随量子位数n呈指数增长.压缩传感理论是由Donoho,Candes等人于2004年提出[3–4],它为降低量子状态估计中的测量次数问题提供了新的思路和解决问题的新手段.该理论指出:如果信号本身是稀疏的,或者矩阵信号是低秩的,那么,通过构造一个满足一定条件的测量矩阵,就可以远少于完备测量的次数,将该信号无损地压缩到低维空间,再通过求解一个优化问题,精确地恢复出原始信号[5].现实中,人们感兴趣的量子系统往往处于纯态或近似纯态[6],这意味量子系统的密度矩阵ρ为低秩r ≪d.此时,可以采用压缩感知理论,只要采用较少的测量次数,就可以精确地重构出ρ.Gross证明采用泡利矩阵进行观测时,由测量结果构造的测量矩阵满足限制等距特性(restricted isometry property,RIP)条件,最少需要mO(rd log d)≪d2个测量值,就可以通过求解一个最优化问题,精确地恢复出密度矩阵[7],并定义采样率为ηm/d2,m为测量次数.

在实际量子测量过程中干扰是不可避免的,当在密度矩阵某些位置的元素中存在稀疏干扰,耦合在测量b ∈Rm中,这种稀疏干扰使得密度矩阵的重构变得困难[8].对于考虑含有稀疏干扰的量子态估计问题,可以将问题转化为:在考虑量子态ρ半正定、单位迹的厄米矩阵的约束条件的情况下,分解求解密度矩阵ρ的核范数,以及稀疏干扰S的l1范数的两个子问题的优化问题[9].2014年,对于量子状态本身存在稀疏干扰的问题,Li首次将交替方向乘子法(alternating direction method of multipliers,ADMM)用于基于压缩传感的量子态重构中,解决了同时包含核范数和l1范数的优化问题[8].该算法求解过程需要计算一个m×d2矩阵的伪逆,计算复杂度为O(d6).2016年,Zheng等人将不动点算法与ADMM结合,提出了不动点方程的ADMM 算法(fixed point ADMM,FP–ADMM)[10].该算法避免了高维矩阵伪逆的求解,将计算复杂度下降到O(md4),提高了密度矩阵的重构精度.2017年,Zhang等人提出结合迭代收缩阈值的算法(iterative shrinkage thresholding algorithm,ISTA)[11],有效地解决带有量子态约束的优化问题,将计算复杂度进一步下降到O(md2),并且能够保证最终的优化结果为全局最优解.不过,ISTA算法每次迭代的步长是固定的,所以算法迭代的收敛速度受到限制.2018年,Zhang等人提出非精确的ADMM 算法(imprecise ADMM,I–ADMM)[12],该算法通过采用近邻梯度法,来近似求解密度矩阵和稀疏干扰的子问题,算法的估计精度得到进一步的提高,并通过仿真实验证明I–ADMM算法优于ISTA算法.非精确的ADMM算法计算复杂度为O(md2).

针对ISTA求解量子状态估计优化问题的不足,本文将改进的快速迭代收缩阈值算法(fast iterative shrinkage thresholding algorithm,FISTA)应用到量子态密度矩阵的估计中.FISTA是一种基于加速算子梯度估计方法优化ISTA的算法,该算法在ISTA的基础上,加入一个加速算子,该加速算子由当前值和前一次值的线性组合构成,以加快算法的迭代速度.本文将FISTA算法应用于5个量子位的仿真实验中,并且将FISTA算法分别与迭代收缩阈值算法(ISTA)、交替方向乘子法(ADMM)、不动点方程的ADMM 算法(FP–ADMM)、非精确的ADMM算法(I–ADMM)4种算法进行性能对比实验,并对实验结果进行分析.

2 含有稀疏干扰的量子状态估计问题描述

考虑一个具有n比特量子系统的密度矩阵ρ,其本身含有稀疏干扰.此时,量子密度矩阵估计问题可描述为:从测量结果b中选取的m个,重构出d×d的低秩的、含有稀疏干扰S ∈Rd×d的密度矩阵ρ.构造观测矩阵为A:Cd×d→Cm,则密度矩阵估计过程中的测量结果可写为bA(ρ+S).

将密度矩阵估计问题转化为一个带有约束条件的目标凸优化问题:

其中:γ为权重因子;ρ为待估计的密度矩阵;∥·∥∗为核范数,定义为∥ρ∥∗∑si,si为矩阵奇异值;∥·∥1为l1范数.最小化∥ρ∥∗和∥S∥1使密度矩阵低秩,且状态本身干扰稀疏.为了简化,定义凸集为0,tr(ρ)1,ρHρ},ρH为ρ的共轭转置,ρ ∈C表示满足量子态约束,并引入示性函数

则式(1)可改写为

对于带有可分离的目标函数和线性约束的凸优化问题式(2),通过引入增广拉格朗日函数

其中:α为惩罚参数,惩罚项可以松弛收敛条件;∥·∥2为l2范数;y ∈Rm为拉格朗日乘子.

此时问题(3)变为一个无约束条件的对增广拉格朗日函数的目标优化问题:

根据ADMM迭代框架,可将待优化问题(4)分解为2个子问题:求解量子密度矩阵、稀疏干扰的优化问题,以及使约束条件为零的拉格朗日乘子的迭代计算公式

这样,就把一个带有约束条件的优化问题,转变为无约束条件的2个子问题的凸优化问题.通过求解优化问题(5),可以求解出含有稀疏干扰的量子密度矩阵估计.这个优化问题求解性能的优劣,取决于所采用的优化算法.下面将先介绍迭代收缩阈值算法,然后在其基础上,提出迭代收缩阈值的快速改进算法.

3 改进的快速迭代收缩阈值算法

3.1 迭代收缩阈值算法

在式(5)所描述的优化问题中,l2范数∥·∥2连续可微,但是,核范数∥·∥∗和l1范数∥·∥1不连续可微,对其求解比较困难.为了解决∥·∥∗不连续可微问题,将式(5)中的ρk+1式乘以然后令f(ρ)∥A(ρ+Sk)这正是软阈值函数(soft thresholding)要解决的优化问题的形式,对其中的平滑项f(ρ)求梯度c1,得到梯度的迭代公式为其中wk是第k次迭代的步长.由于这个算法的整个过程相当于迭代执行软阈值(soft thresholding)函数,所以把它称为迭代收缩阈值算法(iterative soft thresholding algorithm,ISTA).

由于量子密度矩阵有ρHρ的约束,即密度矩阵是厄米的,所以梯度也必须满足厄米矩阵的要求,将梯度ck+1的迭代公式重新定义为

将式(6)代入密度矩阵优化的式(5)中,可以得到密度矩阵估计的迭代公式为

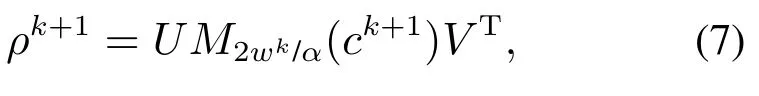
其中:

UMVT为矩阵ck+1的奇异值分解;为软阈值算子,定义为

为了书写方便,定义D2wk/α(ck+1)为奇异值收缩算子:

对于式(5)中的Sk+1的求解,先将其中的Sk+1乘以再令f(S)∥A(ρk+1+S)−b −这也是软阈值函数要解决的优化问题的形式,对其中的平滑项f(S)求梯度d,得到梯度的迭代公式为

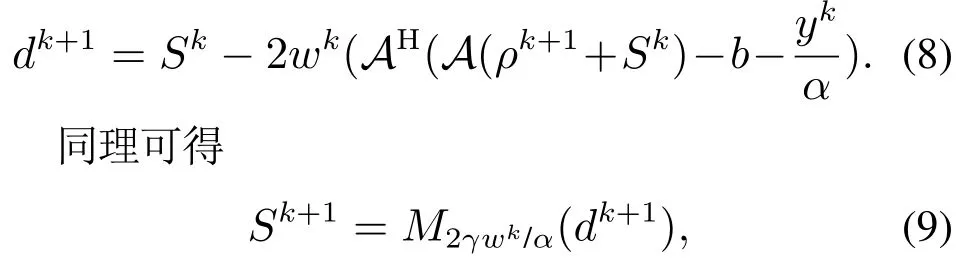
由此可得ISTA算法的迭代公式为

从式(10)中,可以看出:ISTA是梯度下降法的一种延伸,每次迭代只是利用当前点的信息进行梯度估计,然后分别对密度矩阵以及稀疏干扰进行迭代估计,所以算法迭代速度一般.

3.2 快速迭代收缩阈值算法

在ISTA的基础上,通过分别在密度矩阵ρ和稀疏干扰S的计算公式中引入加速算子,来加速收敛速度,进一步降低密度矩阵的估计误差.

首先,引入加速算子z,它是由当前值和前一个值的线性组合构成:

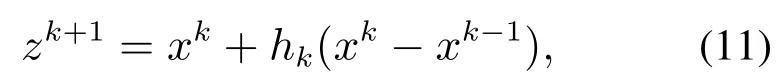
其中:xk,xk−1分别代表当前值和前一次值;xk−xk−1表示搜索方向;hk表示由当前值xk开始,沿着xk−xk−1所构成的搜索方向进行迭代所需要的步长因子,j是可调参数;zk+1表示由当前值xk开始,沿着xk−xk−1所构成的搜索方向进行步长为hk所得到的下一次值.

然后,利用加速算子,分别代入式(10)中含有ρk和Sk中,重新对含有稀疏干扰的量子状态进行估计,由此可以分别得到改进后的状态进行估计迭代公式为

以及稀疏干扰的估计迭代公式为

其中:hk−1j×权重γ可以设置为wk和j需要根据实际具体情况来调节参数.

由于FISTA算法是在ISTA的基础上,通过加入一个由当前值和前一次值的线性组合构成的加速算子(11),该加速算子是随着迭代次数k的增加,而每次增大hk(xk−xk−1),起到对当前值与前一次值之差的进一步的补偿作用,因而能够加快算法的迭代速度.理论上已经证明[13]:ISTA和FISTA的计算复杂度都为O(md2);ISTA算法的收敛速度为O(1/k),而FISTA的收敛速度为O(1/k2).FISTA的收敛速度比ISTA快1/k倍.

4 数值仿真实验及其结果分析

本节将对一个5量子位系统的密度矩阵,采用FISTA算法进行状态估计的数值仿真实验.做两个实验:第1个实验为:不同采样率η下,对FISTA和ISTA两种算法进行仿真实验,比较仿真实验的性能结果;第2 个实验为:固定采样率50%下,对ADMM,FP–ADMM,ISTA,FISTA和I–ADMM 5种算法进行仿真实验,并对实验结果进行了性能的比较.

实验中算法性能的评估指标为:估计出的密度矩阵ρ与真实密度矩阵¨ρ之间的归一化误差Error:Error

4.1 FISTA和ISTA算法的估计误差对比

本实验将在采样率η分别为25%,50%,100%,固定迭代次数为100次,分别采用FISTA以及ISTA两种算法,对5量子位密度矩阵进行状态估计.

两种算法涉及的可调参数有权重γ、惩罚参数α、梯度下降步长wk,FISTA多一个加速算子里的可调参数j.根据算法的收敛要求,通过实验结果对参数的设置进行优化调整,最终的参数设置如表1所示.在不同采样率η下,两种算法对密度矩阵的估计误差Error随迭代次数的变化结果如图1所示.

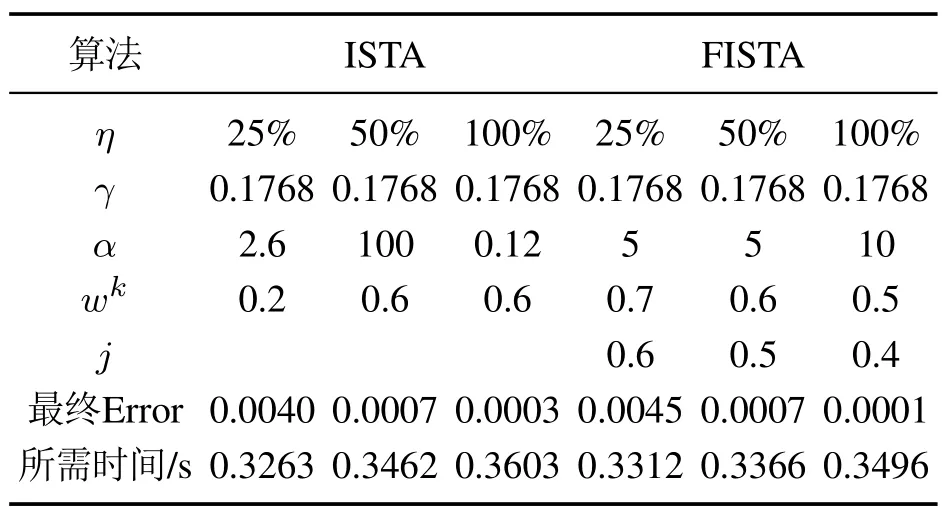
表1 两种算法对比实验中的最优参数设计Table 1 Optimal algorithm setting in two experiments

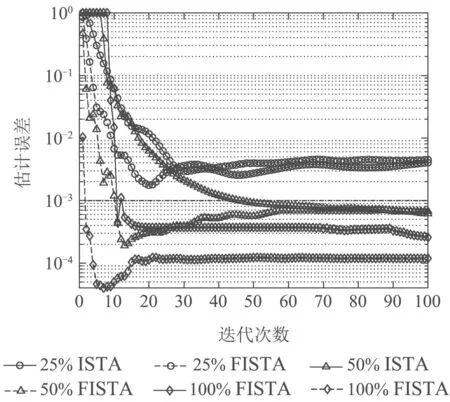
图1 两种算法的估计误差对比Fig.1 Comparisons of estimation errors of two algorithms

从图1的量子状态估计误差的实验结果中可以看出:

1)在状态估计达到稳态之前的暂态过程中,FISTA明显优于ISTA.在相同采样率和相同迭代次数下,FISTA的估计误差一直小于ISTA的估计误差.

2)随着采样率η的增加,ISTA和FISTA两种算法的稳态估计误差都在降低.相同采样率下,FISTA达到的稳态估计误差比ISTA的稳态估计误差低;采样率为25%和50%时,FISTA 比ISTA 稳态估计误差略低,采样率为100%时,FISTA的稳态估计误差明显低于ISTA.相同采样率下,FISTA比ISTA以较低迭代次数达到较高量子状态重构精度.采样率为25%时,ISTA需迭代46 次(0.1799 s)达到最低估计误差0.0025;FISTA 需迭代20 次(0.1153 s)达到最低估计误差0.0018,迭代次数明显更少,估计误差明显更低;采样率为50%时,ISTA需迭代44次(0.1939 s)达到不高于0.0010 的估计误差0.0010;FISTA 需迭代12 次(0.0867 s)达到不高于0.0010 的估计误差0.0002,FISTA明显更优;采样率为100%时,由图上曲线直接可以看出,FISTA的估计误差随着迭代次数的增加在降低,一直低于ISTA的估计误差.

3)暂态达到的最低估计误差低于稳态时的估计误差.可见,并不是迭代次数越多,状态估计达到的估计误差就越低越好,应在估计误差达到最小值时就停止实验,取当时的最小值为状态估计结果.

4.2 5种算法的估计误差对比

本实验中将分别采用5 种算法:ADMM,FP–ADMM,ISTA,FISTA和I–ADMM,对5个量子位的密度矩阵进行状态估计.实验中,采样率η固定为50%,迭代次数选为1000次.ADMM算法中的2个参数分别取:梯度步长τ1τ20.1;FP–ADMM算法中的两个参数分别取:权重γ1、惩罚参数α0.04;I–ADMM算法中的3个参数,分别取:梯度步长τ10.99,τ20.6,惩罚参数α1.399.FISTA和ISTA两个算法的参数与第4.1节中对应的实验参数选择一致.

实验所获得的估计误差Error随迭代次数增加的变化结果如图2所示.

图2 5种算法的估计误差对比Fig.2 Comparisons of estimation errors of five algorithms

从5种算法的量子状态估计误差的结果图2中可以看出:

1)在5种算法中,ADMM算法是最差的,FISTA算法是最好的.同一采样率η下,本文的FISTA算法达到最小估计误差0.0019的量子状态重构所需要的最少迭代次数为13次(0.0882 s),目前最优的求解存在稀疏干扰的量子态估计的I–ADMM优化算法的达到最小估计误差0.0017 所需要的最少迭代次数也为13 次(0.1077 s),最少迭代次数相同,但FISTA算法所需迭代时间0.0882 s明显低于I–ADMM的所需迭代时间0.1077 s.

在相同的采样率η的情况下,分别采用ADMM,FP–ADMM,ISTA,FISTA和I–ADMM 5种算法完成1000次迭代所需时间分别为:137.4342 s,11.6561 s,2.7510 s,2.7208 s,3.4330 s,FISTA 算法所需时间最短、速度最快.

由图2可知,本文的FISTA算法估计误差明显低于ADMM,FP–ADMM,ISTA 3 种算法,和I–ADMM 算法估计误差接近,由于FISTA算法迭代时间比I–ADMM算法快,故FISTA算法最优.

2)同一采样率η下,FP–ADMM,ISTA,FISTA和I–ADMM 4种算法达到的稳态误差相接近,且都远低于ADMM的稳态误差.

ADMM只是一种求解优化问题的计算框架,将大的全局问题分解为多个较小、较容易求解的子问题,并通过协调子问题的解而得到全局问题的解.每一个子问题和如何有效求解,需要根据f(x)和g(z)具体形式来确定.ADMM算法中求解Frobenius范数项最小时,需要计算一个矩阵的伪逆,这样的求解方法会导致巨大的运算量.ADMM算法的重构精度相对于完备测量重构的精度还有待于进一步提高,对于较高比特的量子系统(例如7比特),ADMM算法重构时间要以天为单位计算,算法速度仍有待于进一步提高.

FP–ADMM通过近邻算子求解基于压缩传感的量子态估计优化问题的最优解满足的不动点方程,再采用迭代的方式求解最优解,避免了基于压缩传感的量子态估计的ADMM算法中的大规模矩阵伪逆运算,从而大幅度地减少在密度矩阵重构应用中的计算时间.

I–ADMM的主要思想是通过近邻梯度法近似求解子问题,非精确求解密度矩阵和稀疏干扰相关的子问题从而获得闭式解,将计算复杂度从Li的ADMM的O(d6),Zheng 的FP–ADMM 的O(md4),降低到O(md2).此外,该算法采用可调步长更新拉格朗日乘子以加速收敛.

ISTA通过梯度下降和近邻算子操作得到ADMM子问题的解,再代入ADMM迭代框架得到全局问题的解,运算过程涉及最大的计算量为m×d2的矩阵A和d2×1的向量相乘,计算复杂度为O(md2),因此ISTA算法可以大幅度减少计算时间和存储空间.

FISTA是在ISTA基础上的优化,加快了收敛速度,收敛速度由O(1/k)变为O(1/k2).

3)ISTA和I–ADMM两种算法的暂态达到的最低估计误差低于稳态时的估计误差.可见,并不是迭代次数越多,状态估计达到的估计误差就越低越好,人们应在估计误差达到最小值时就停止实验,取当时的最小值为状态估计结果.

5 结论

本文所提出的FISTA算法,可以高效精确地求解出量子状态本身含有稀疏干扰的情况下的估计值.通过5量子位密度矩阵仿真实验表明,FISTA算法收敛速度更快,量子状态估计误差更小,更加有效地提高了求解量子状态估计优化问题的效率和状态估计精度.实验结果还表明,在量子态估计迭代过程中,当判断出获得估计的最小值时,就应当停止迭代.