基于增量式策略强化学习算法的飞行控制系统的容错跟踪控制

任 坚,刘剑慰,杨 蒲

(南京航空航天大学自动化学院,江苏南京 211106)

1 引言

随着航空航天技术的不断发展,飞行控制系统的规模变得越来越庞大,系统的复杂度也不断地增加.在飞行控制系统不断进步的同时,系统的稳定性也面临着巨大的挑战.任何类型的故障都可以导致系统性能的折损甚至是瘫痪,造成控制系统的不稳定,从而带来巨大的损失.因此,如何减小甚至是消除系统故障所带来的危险是一个值得研究的问题,为了克服传感器、执行器和其他部件的故障,国内外学者们在故障诊断与容错控制这一研究方向上做出了很多的努力.

1993年,国际上出现了第一篇关于容错控制的综述性论文[1].针对处于故障下的被控系统,可以采取可靠镇定控制的方法,通过并联多个补偿控制器同时控制被控系统,使系统发生故障时依旧保持系统的稳定[2].此外,Gopinathan和Boskovic等人提出了一种完整性控制的思想,当被控系统发生传感器或执行器故障时,通过完整性控制的方法仍能够保证系统的稳定性和安全性[3].上述的方法均为被动容错控制,虽然被动容错控制被证明了具有一定的鲁棒性,不需要对系统的故障进行在线监测与评估,可以在飞行控制系统执行器发生可能的失效故障情形下正常飞行,但是被动容错控制还是存在一定的保守性.相较于被动容错控制,主动容错控制通过对故障的在线评估与控制信号的重构保证了系统的稳定运行.在主动容错控制领域,主动容错控制器通过故障监测与诊断单元(fault detection and diagnosis,FDD)来实时获取在线的故障信息,并根据在线故障信息调整控制系统的参数或结构,对控制器进行重构设计,是系统在发生故障后还能正常运行[4–6].此外,文献还可以采用模型跟随重组的方法,通过对输出误差信号的实时跟踪已达到容错控制的目的,此方法虽然为主动容错控制方法,但不需要FDD单元,大大方便了系统的设计[7].

近年来的研究工作大多聚焦在系统控制器的设计上,大多采用基于模型的方法对系统控制器进行重构[8–22],而由于科学技术的发展,飞行控制系统的复杂度越来越庞大,这也为对飞控系统的数学建模带来了巨大的挑战,由于基于模型的方法能够成功实现的前提是对系统的精准建模,所以随着控制系统越来越复杂,基于模型的方法的局限性也体现了出来.而随着大数据和人工智能的兴起,国内外的研究者也开始将目光转投向基于数据的跟踪控制方法[23–27],由于基于数据方法的较高工程应用价值,最近几年也引来了越来越多业界的关注.Ng等人通过强化学习的方法实现了直升机的倒立飞行[28].Williams对于强化学习控制器的状态—–动作对的采样方法进行了改进,通过随机采样来加快学习的收敛速度[29].Wang和Liu等人提出了一种优化的强化学习容错控制器的训练方法,可以大大节省计算资源[30].相较于Wang和Liu 等人提出的确定性策略,本文创新性地提出了增量式策略方法,将使强化学习方法能够较好地完成容错控制任务.

本文将针对执行器故障与传感器故障情况下的飞行控制系统,基于强化学习的Q-learning方法,提出了一种主动容错控制方案.采用增量型策略的强化学习方法,研究发生多种故障(执行器故障与传感器故障)下的主动容错控制技术,相较于基于模型的主动容错控制的方法,采用强化学习方法进行容错控制,若系统故障产生,强化学习控制器可以提取系统实时产生的数据的特征,从而获取当前状态的故障信息,并通过某种策略让控制器做出在当前状况下能做出的最优策略,使得系统能够保持稳定,从而正常运行.由于系统故障的不确定性,无法通过一个确定性的策略做决策,本文采用了优化的增量型策略代替了确定性策略,通过在系统容错控制过程中控制器对增量型策略的迭代来重构控制器,从而使控制器能够渐进逼近最优解.与传统的强化学习的确定性策略不同,由于控制系统故障发生的不确定性,通过确定性的固定策略对控制系统进行容错控制的效果肯定会差强人意,本文提出的增量式策略便能解决这个问题,通过对上一步策略的保持并进行新一轮的更新从而达到上面所说的逼近效果的思想达到容错控制的目的.本文中的强化学习方法主体采用Q-learning算法结构,通过对数据的实时采集在线更新决策网络,使得控制器Agent能够准确地预判下一步策略.同时,由于强化学习方法需要使用当前状态与动作作用下的下一个状态信息,本文将采用状态转移预测网络对连续的控制系统的下一步状态进行预测,并通过存储地历史信息来对状态预测网络定期做训练更新,从而实现对决策网络实时的更新.

2 系统故障问题描述

考虑一类连续飞行控制系统为

其中:x ∈R4×1为系统的状态,x,其中θ为俯仰角变量,φ为滚转角变量;u[u1··· u4]T为控制输入;系统矩阵A∈R4×4,B ∈R4×1,C ∈R1×4;y∈R为系统输出变量;ϕ(t−t1)fa(t),ϕ(t−t2)Ffs(t)分别表示飞行控制系统中的执行器故障和传感器故障,t ∈R+,其中: fa(t)为未知的执行器故障偏置值,Ffs(t)为未知的传感器故障的偏置值,其中: F ∈R1×4,fs(t)∈R4×1; ϕ(t −tf)定义为故障产生时间定义函数:

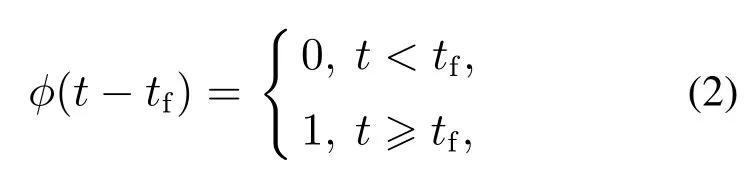
其中tf为飞行控制系统中的未知故障产生的时间,在本文中通过ϕ(t −tf)函数表示系统的突发性故障(在时间tf之后故障发生).在开始设计控制器之前,需要为研究对象做一些假设.

假设1控制系统中存在可以被测量的状态变量,在控制系统运行过程中,系统的部分甚至所有状态变量是能够被观测的.

假设1保证了系统中状态和输出的可测量性,这对基于数据的容错控制技术至关重要,这使得强化学习控制器可以通过控制系统运行时的数据去评估奖励函数并更新训练价值网络,从而使控制器做出最好的调整,使控制系统处于当前最优的状态.如果系统的某些状态或者是输出不能用传感器技术去测量,也可通过观测器和滤波器技术进行得到,这种情况也满足假设1.

假设2存在已知的正数常量ξ,δ >0使得执行器故障fs(t)和传感器故障Ffs(t)满足

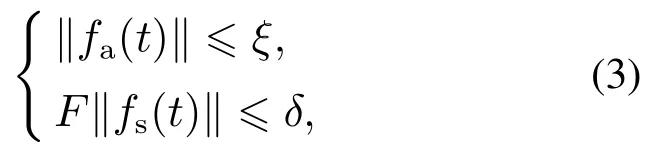
其中∥·∥表示欧几里得范数.

假设2保证了故障未知但满足范数有界的条件,由于本篇文章采用的是增量式策略更新重构信号的方法,所以只有满足执行器故障有界,才能保证容错控制器能够得到最终最优的策略.

假设3在系统正常运行状态下,系统将沿着参考输出信号轨迹yd(t)做跟踪运动.于是,在本文中假设参考输出信号yd(t)∈Ωy,其中:Ωy是一个有界的集合,而yd(t)是一个属于集合Ωy中的光滑曲线函数,例如正弦信号等.

本论文的目标是设计出基于强化学习方法的主动容错控制器,通过增量型策略对发生未知故障的飞行控制系统进行容错控制,利用增量型的策略较快的逼近的最优策略,以达到做出对控制系统最优的调整,而实现以上目标可以转换成满足一下条件:1)通过对系统损失指标的最小化,从而做出当前最优的动作;2)系统输出y可以快速地跟踪参考信号yd,并且整个闭环系统的所有状态变量均是有界的.

3 基于强化学习的主动容错控制器设计

本节将对主动容错控制器系统状态进行定义,设计控制器奖励函数,并对增量型策略进行介绍.针对连续系统的状态预估,介绍状态转移预测网络方法.

3.1 容错控制器系统状态与状态—动作奖励函数

系统状态是从控制系统中选出的能够反应控制系统运行状态的变量,它能够反应系统当前的运行状况,容错控制器通过系统状态抽取有用的特征,将其作为容错控制器进行决策的重要依据.将容错控制系统状态定义为飞行控制系统的姿态角:

选取的状态参数依据为本文所采用的仿真平台所能采集到的状态量,其中ϕ,θ分别为实验平台飞行器的滚转角和俯仰角,这些状态参数将作为评价网络的输入从而得到奖励值.状态—动作奖励函数可以看作容错控制器对不同策略好坏的打分,而这个分数便是系统损失指标的依据,通过对其最小化决策出当前最优的策略进行控制系统的容错,于是奖励函数直接影响着控制器的决策效果的好坏,针对控制系统的跟踪控制,定义当前状态–动作奖励函数J(St):

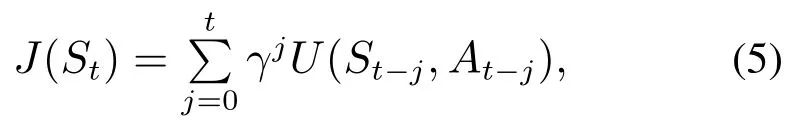
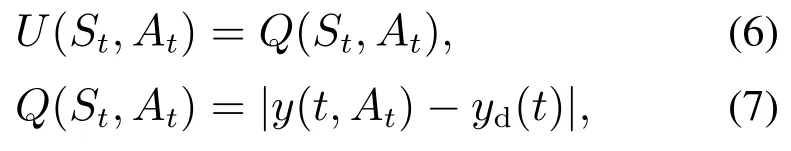
其中y(t,At)表示在时刻t下,采用动作At所得到的系统输出,因而Q(St,At)则表示在t时刻系统状态为St,采用动作At系统的输出与期望输出之间的误差的绝对值,而设计控制器的目的便是选取动作At,使得此时的状态–动作奖励函数最小.

3.2 增量型策略方法

传统的强化学习方法运用在非控制领域常采用确定性策略,谷歌DeepMind团队[31]采用深度强化学习方法研发出了人工智能象棋Agent,由于每步策略独立的前提下,因而采取的策略是确定性的策略.而相较于象棋,发生故障的控制系统由于故障的未知性,采用确定性的策略会使容错控制器的适用范围受到很大的限制.本文提出了一种基于增量型策略的强化学习Q-learning算法,从而通过策略地叠加实现最优策略地渐近逼近,同时丰富了策略的多样性,充分发挥了强化学习Agent的自我学习特性.

3.2.1 策略选取方法

本文中采取参考文献[32]中的ε-greedy策略,在控制器的训练过程中引入ε-greedy因子对策略网络进行更新,而ε-greedy因子表示此次策略选择随机策略的概率.同时,因子ε采取退火操作,从1退火到0.因此在退火初期,控制器选择随机策略的概率较大,此阶段为初步探索阶段,随着策略迭代到后期,系统便主要选择此时控制器认为的最优策略对控制系统进行调整.而在训练过程趋于结束,评价网络所能做出的决策已经十分成熟后,ε将退火到零,则决策网络将采取确定的决策策略,选取控制器认为最优的策略.ε-greedy策略具体表示如下:

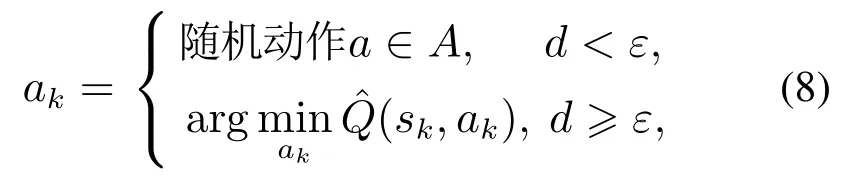
其中:a为当前控制器所做出的动作;动作集合A为一个集合,集合中的元素为控制器所有可能选取的策略.与立即回报函数Q(sk,ak)相区别,为评价网络对当前状态为sk,当前策略为ak情况下奖励值的预估.

3.2.2 增量型策略

容错控制器的输出Ak为系统的重构方案,对于本文中的实验平台,根据前期的实验分析,其可用的重构方案由不同的故障决定,数量一般只几种到十几种不等,并且容错效果较好.因此,本文参考文献[33]的方法,可以通过枚举的方法将有限的配置方案进行增量式的累加更新,从而更新得到最优策略输出.本节将介绍控制系统所采用的配置方案的设计:

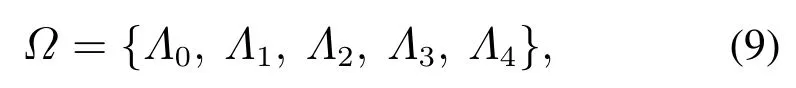
其中集合中的Λn为系统中可选的配置方案.如表1所示,动作集合中的策略均为增量型,分为反向与正向,控制器通过补偿的方法进行系统的容错控制.控制器选取了相应的动作之后将此策略叠加到当前的动作值当中,并针对传感器故障与执行器故障设计了具体的策略,在本文中增量型策略采取步进值为±0.0002,精度取决于传感器和执行器的性能指标并且决定了控制器训练收敛的速度和策略最优的准确性.

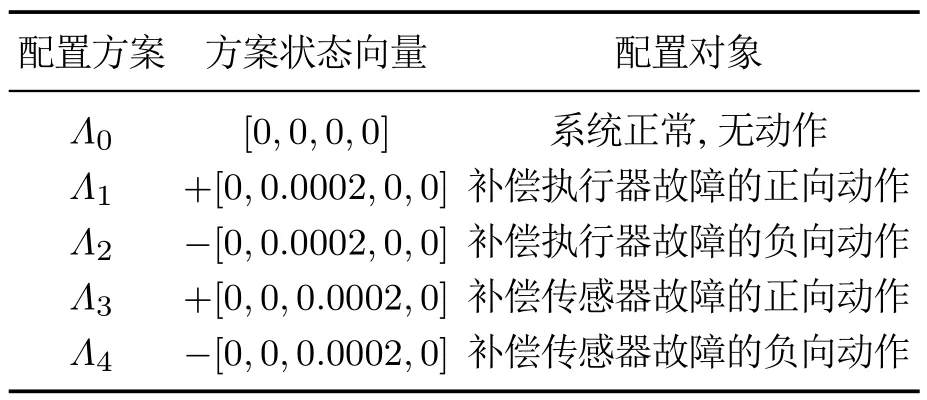
表1 动作A集合中的动作方案Table 1 Strategy scheme in action A set

4 强化学习主动容错系统结构及算法实现

4.1 评价网络的实现

本文方法采用神经网络对系统Q-learning函数进行建模拟合,计算出Q-learning函数的近似值,神经网络的输入为X[S A]T,并采取梯度下降法[34]对其进行权值更新,输出层权值的更新法则如下:

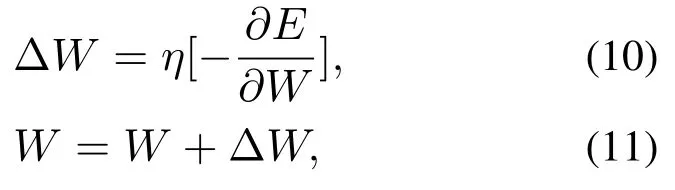
其中:其中函数E是在当前状态和容错策略下所得到的奖励函数reward值与当前系统状态的下一个状态得到的奖励函数reward值的误差,η为训练学习率,通过梯度下降算法对误差函数E进行微分并且逐层向上传递,并通过公式(11)此方法实现评价网络权值的更新.

如图1所示,评价网络的结构为含有隐藏层的多层神经网络,相比于传统的基于模型的容错控制器,评价网络的思想是将控制系统实时产生的状态数据进行采集,并通过神经网络的方法自动提炼出系统数据当中的特征来对系统状态进行辨识,而图1中的输出y便是神经网络对故障辨识后所得出的策略结果.本文中评价网络通过强化学习Q-learning算法对评价网络进行训练与更新,将采集得到的系统状态值和容错控制策略作为评价网络的输入样本得到当前状态与所选择策略的奖励值作为容错控制器选取策略的依据,进而选取最优策略交给执行网络进行下一步操作.

图1 容错控制器评价网络结构图Fig.1 Fault tolerant controller evaluation network

4.2 执行网络的实现

执行网络的输出A为系统的决定的容错方案,对于飞行控制系统,其配置方案可由其系统状态量进行预估,在状态S下,动作A由以下步骤实现:

步骤1对于系统的容错调整方案,通过评价网络计算对应的不同动作ak所对应的奖励

步骤2输出当前评价网络预估得到的容错调整方案at:

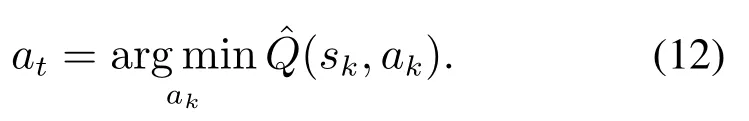
上述步骤是在评价网络训练结束之后对执行网络的步骤的描述.

4.3 状态转移预测网络

由于本文研究对象为连续的飞行控制系统,而强化学习算法评价网络的更新学习过程中,需要得到当前状态下所作出策略而得到的下一个状态值,所以对于本文中的控制器而言,通过当前的状态与动作预估出所得到的下一步状态是十分重要的.所以针对这一需求,本文提出了一种状态转移预估网络的方法,其结构类似于评价网络的多层神经网络,对输入样本为状态与策略,输出为此状态与策略所得到的下一个状态进行拟合训练,通过当前的状态动作对,预估出下一步所得到的状态.状态转移预测网络的输入X[ScurrentAcurrent]T,输出Y[Snext]T.整个训练过程是将历史的系统状态与动作存储到计算机,然后每隔固定的迭代次数将存储的数据作为数据集对状态转移预测网络进行评估.

4.4 容错控制器迭代学习算法

基于强化学习的主动容错控制器的结构如图2所示,其中:Scurrent是系统当前在动作Acurrent下通过传感器观测到的状态值;Acurrent是对控制系统控制器做出调整的重构信号,并不是系统的输入;U(Scurrent,Acurrent)为系统的实际输出与期望输出之间的误差.评价网络通过每一轮更新误差来进行重新训练,由于神经网络训练往往会陷入局部极小值,进而导致训练误差越来越大,所以采用ε-greedy因子对神经网络的训练过程进行优化.ε-greedy因子表示系统在决策过程中选择随机动作的概率.在训练的过程中,将ε从1慢慢退火到0,在训练的初期,系统更倾向于去不断地“试错”,选择随机的策略,到了后期,系统开始慢慢依赖评价网络所做出的评估,整体的训练算法如下:

1)初始化Q-learning评价网络,神经网络随机初始化参数,神经网络的输入数据为系统的状态和当前采取的动作序号,输出为当前状态与在此状态下采取动作所获得reward奖励值U(Scurrent,Acurrent);

2)初始化历史状态存储单元,用来存储每个步长的状态–动作对;

3)通过控制系统历史运行的数据对状态转移预测网络进行隔代更新,用来通过当前的状态和动作值来预测下一个状态值;

①采集到当前状态St:以ε的概率在所有动作集合中随机选择动作,以(1 −ε)的概率选择使reward值(在本文中就是系统的实际输出与期望输出之间的误差)最大化的动作记当前的状态St和动作At值所得的奖励为U(Scurrent,Acurrent);

②通过①步中的Scurrent,Acurrent和状态转移预测网络得到所得到的下一个状态Snext,求出当状态Snext下预估得到最大奖励的Anext,并将当前Scurrent,Acurrent存储到集合Q;

③然后得到最新的奖励真实值

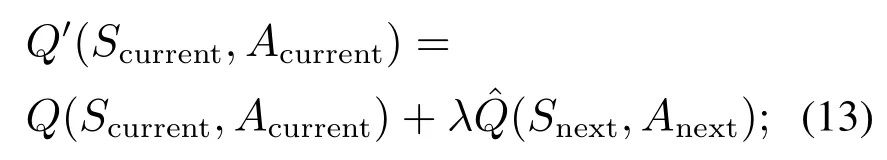
④Agent采取增量型动作Acurrent叠加到现有动作中输入到系统中去;

⑤选择每100步通过存储在历史状态存储单元中的数据对状态转移预测网络进行更新,更新误差函数E为当前状态和容错控制策略所得到奖励的真实值Q′(Scurrent,Acurrent)与评价网络预估值Acurrent)之差:

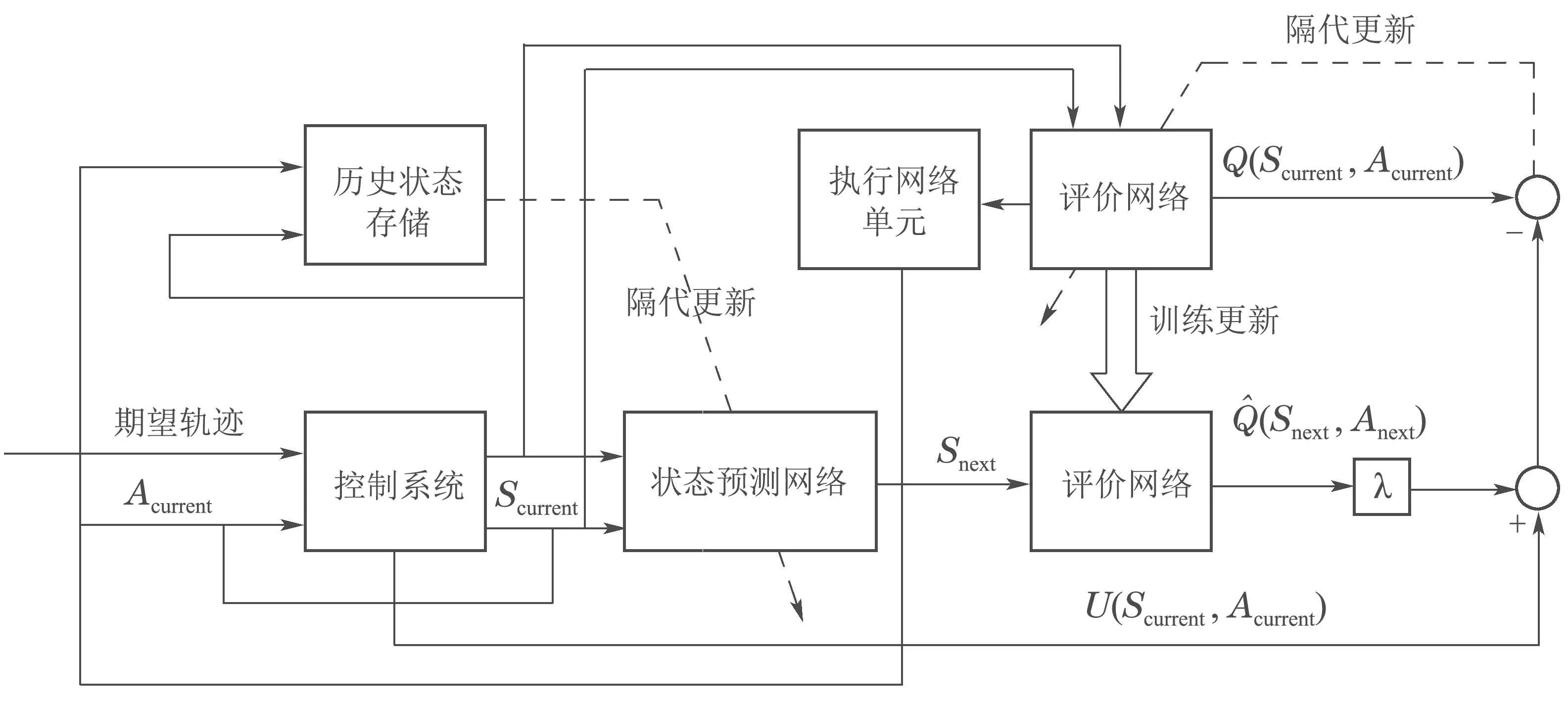
图2 主动容错控制器结构图Fig.2 The structure of active fault tolerant controller

5 仿真验证

5.1 仿真平台介绍

本篇论文通过南京航空航天大学“先进飞行器导航、控制与健康管理”工信部重点实验室的飞行器故障诊断实验平台进行仿真与实物验证,飞行控制仿真平台可以实现飞行器姿态角的测量、飞行控制系统算法和飞行姿态故障诊断算法的实验与研究,并且具有控制系统设计开发,硬件测试和软件仿真等功能.仿真平台详细结构见图3所示.

此仿真实验平台利用角动量的原理来平衡和保持姿态的方向角.在仿真系统内侧存在着一个惯量盘,并安装于图中1处万向节内,1处万向节安装在图中两处万向节内部,并通过一个方形支架固定在外壳上,可以沿着竖直方向任意角度转动.每个万向节通过滑环进行连接,从而使3个轴方向上可以自由地绕轴向转动.仿真平台通过机械方式使得各轴方向可以独立旋转,同时仿真平台的各个方向都配备了高精度的光电编码器,编码精度(倍频后)不低于4000 count/rev,用来精确的测量姿态角等数据,而本片论文中所需的数据将通过仿真平台内置的传感器进行读取.

图3 飞行器故障诊断实验平台实验系统Fig.3 Aircraft fault diagnosis experimental platform

5.2 实验平台参数介绍

5.2.1 实验平台模块介绍

本篇论文所采用的平台通过MATLAB软件将硬件平台与Simulink软件仿真平台进行连接,通过配备在硬件实物平台中的精密传感器通过仿真平台中的硬件在回路(hardware-in-loop,HIL)模块将实时的平台数据传入仿真平台中的控制系统模块中进行软件与硬件的同步运行,当运行仿真平台时,HIL模块、增益放大器、频率滤波器和电源模块在内的全部模型便同时启动,仿真系统模型中的参数细节如图4和图5所示.

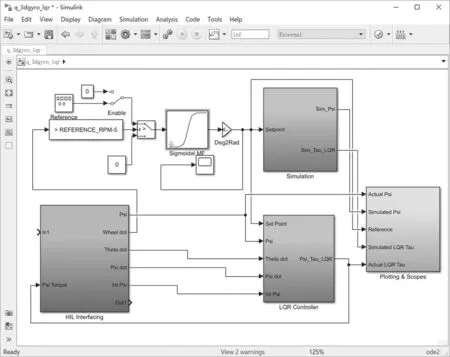
图4 Simulink控制系统模块界面Fig.4 The interface of Simulink control system module

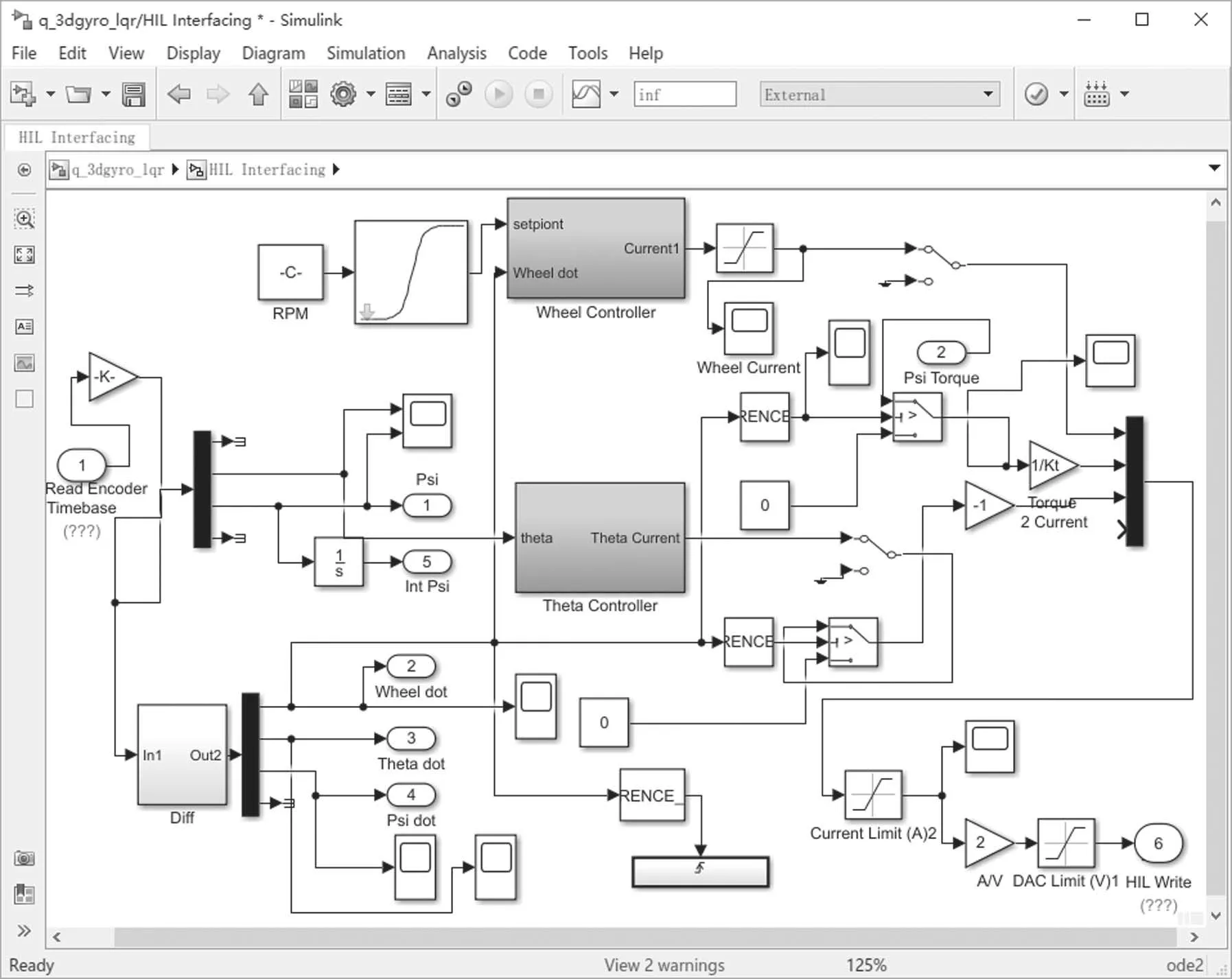
图5 Simulink系统硬件在回路模块界面Fig.5 The interface of Simulink system HIL module

5.2.2 实验平台控制系统模型介绍

实验平台中系统模型的参考坐标系如图6所示.

图6 实验平台参考坐标系Fig.6 Reference coordinate system of the experimental platform

如图6所示,图中箭头1所指的万向节表示飞行器的俯仰角,图中箭头2所指的万向节表示飞行器的滚转角,角速率运动方程式为

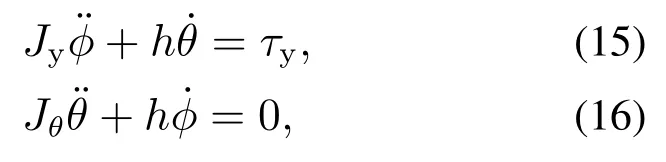
式中:Jϕ0.0036 kg·m2,Jθ0.0226 kg·m2,h0.44 kg·m2/s; Jϕ表示滚转轴的转动惯量;Jθ表示俯仰角的转动惯量;h是通过平台硬件转子的惯性矩阵及其速度计算得到.图6中箭头3所指的外部矩形框架下的驱动轴是滚转轴,而τy是系统中的控制输入在滚转轴施加的扭矩.实验平台的控制系统的线性状态方程表示为

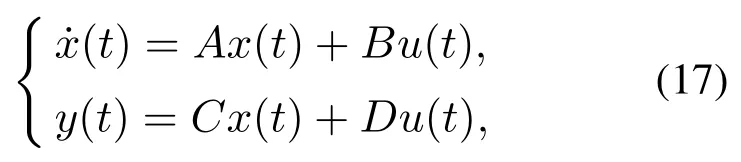
其中: x(t)表示系统状态量,u(t)表示系统的控制输出.定义状态和输出如下:

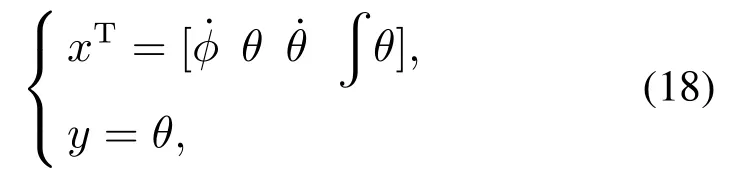
其中ϕ,θ分别为实验平台飞行器的滚转角和俯仰角.本篇论文通过对控制系统中的硬件在回路模块中进行故障注入,并通过平台硬件传感器采集到实验平台在故障与非故障情况下的系统的状态数据.从而通过采集到的数据对强化学习评价网络进行训练,使容错系统网络参数能够满足容错目标.

5.3 执行器故障数字仿真与物理平台实验验证

图7分别为系统发生故障时容错控制器的数字仿真容错效果曲线和容错过程中控制输出变化曲线.从容错效果曲线图中可以看出当故障发生后,容错控制器克服了故障产生的影响,在t8.5 s左右,系统姿态在发生故障的俯仰角上已经基本恢复稳定.

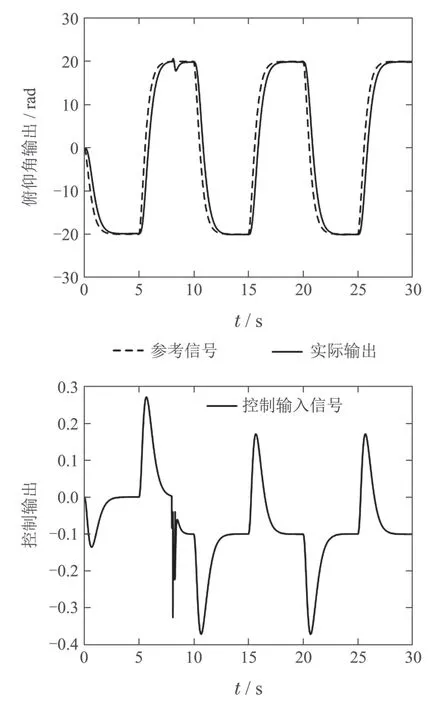
图7 数字仿真容错过程控制系统容错效果和反馈输出变化(执行器故障)Fig.7 Fault-tolerant effects and feedback output changes of digital simulation fault-tolerant process control systems(actuator failure)

从图8的评价网络训练曲线上可看出评价网络不同于普通的神经网络训练网络的递减趋势,因采用εgreedy策略选取方法,策略网络会以一定概率去做探索,所以网络的训练误差曲线会呈现出不稳定的状态.

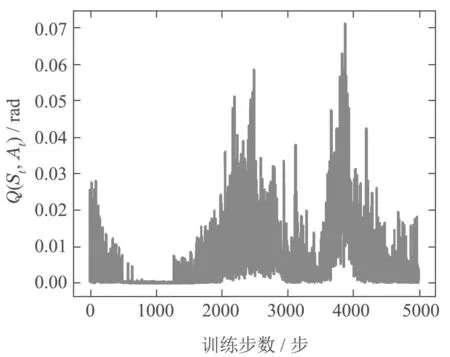
图8 强化学习控制器评估网络的误差训练曲线Fig.8 The training curve of reinforcement learning controller evaluation network error

通过数字仿真验证了实验方法的可行性之后,将本篇论文中的方法运用在物理仿真平台上,强化学习的评价网络参数由数字仿真所得到的结果提供,具体的效果图如图9和图10所示,可以看出当系统发生故障后系统姿态发生偏移,此时通过评价网络得出了最优的容错控制方案,并根据此时评估得到的容错控制方案对系统进行容错控制,可以看出系统姿态基本恢复正常,并能够跟踪目标轨迹.

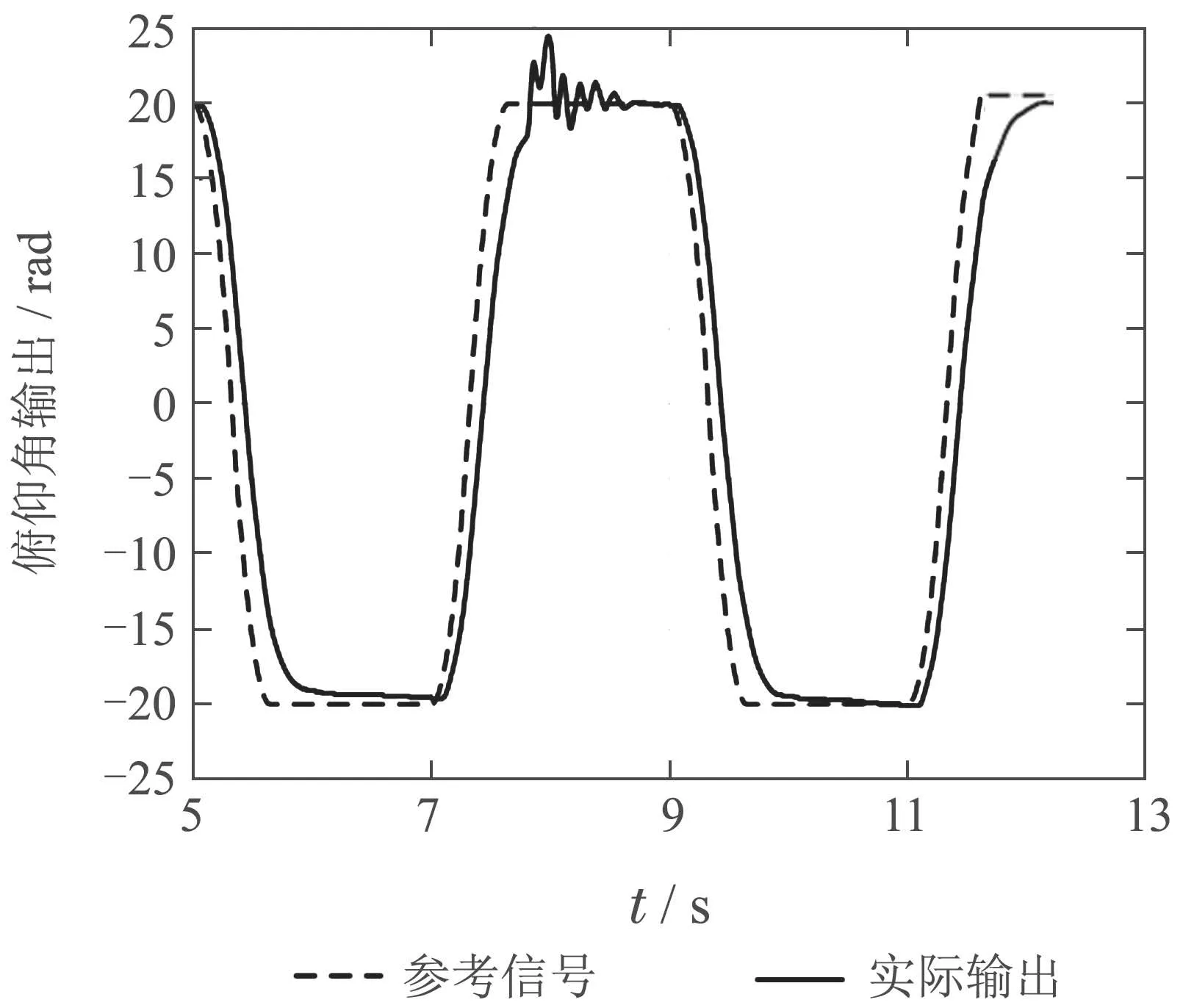
图9 物理平台执行器故障容错俯仰角输出Fig.9 Pitch angle output during fault tolerance of physical platform actuators

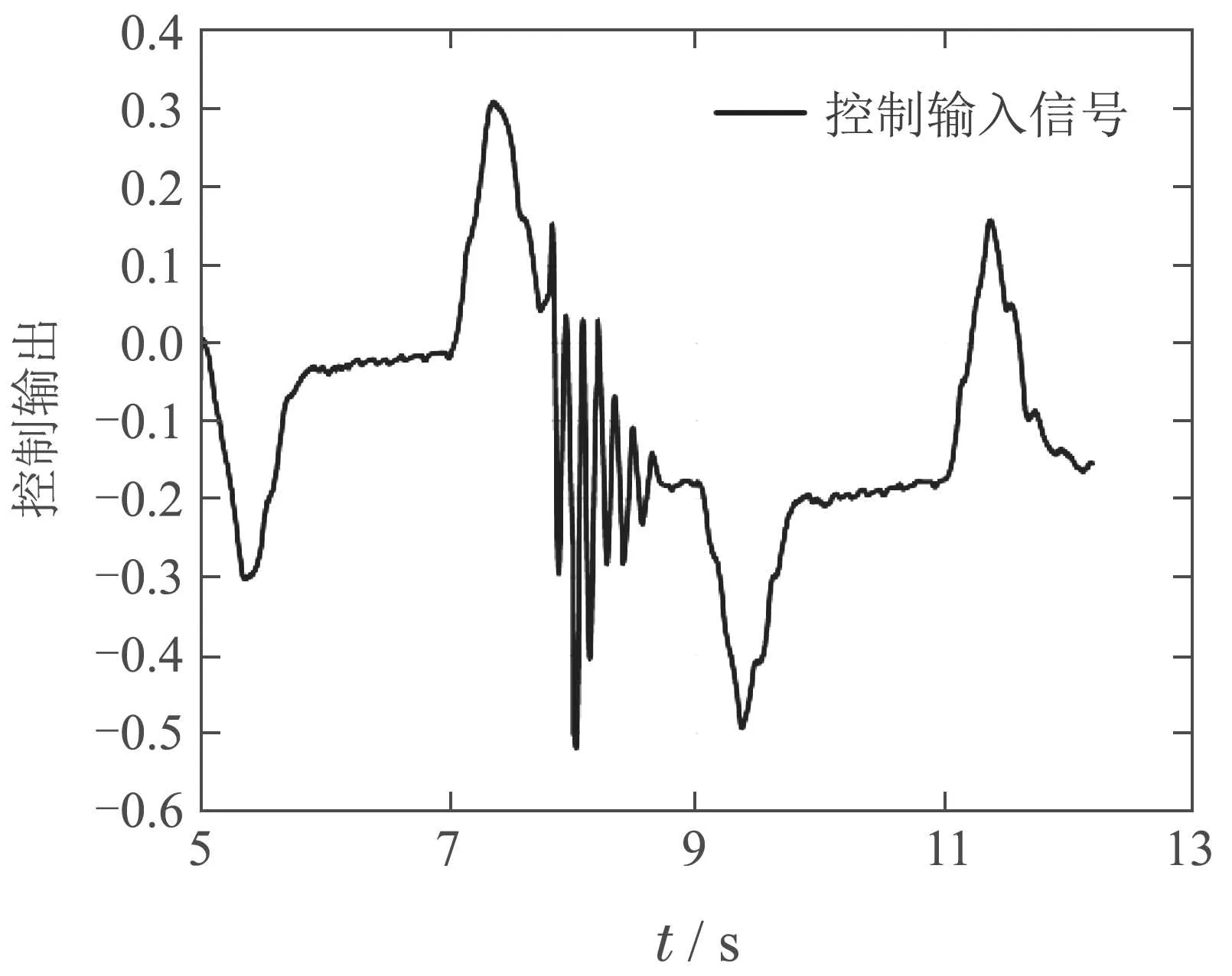
图10 物理平台容错控制反馈输出Fig.10 Control feedback output in the physical platform fault tolerance process

如图11所示,相较于本文中的方法,传统的强化学习算法由于确定性策略的局限性,只能通过固定数量的策略进行策略的选择,导致实际容错效果与理想效果有较大误差.

图11 传统强化学习方法下执行器故障容错俯仰角输出Fig.11 Pitch angle output in actuator fault tolerant process under traditional reinforcement learning method

5.4 传感器故障数字仿真与物理平台实验验证

图12展示了本文介绍的主动容错控制器在发生传感器故障后数字仿真的效果图.从图12可以看出,在传感器故障发生之后,在t8.2 s左右,系统姿态已经基本恢复稳定.

将通过数字仿真验证可行后的网络参数运用到实际物理平台上的仿真效果如图13和图14所示,可以看出本篇论文中的方法对于实物平台也具有良好的容错效果.而如图15所示,运用确定性策略的传统强化学习方法,容错效果并不理想.

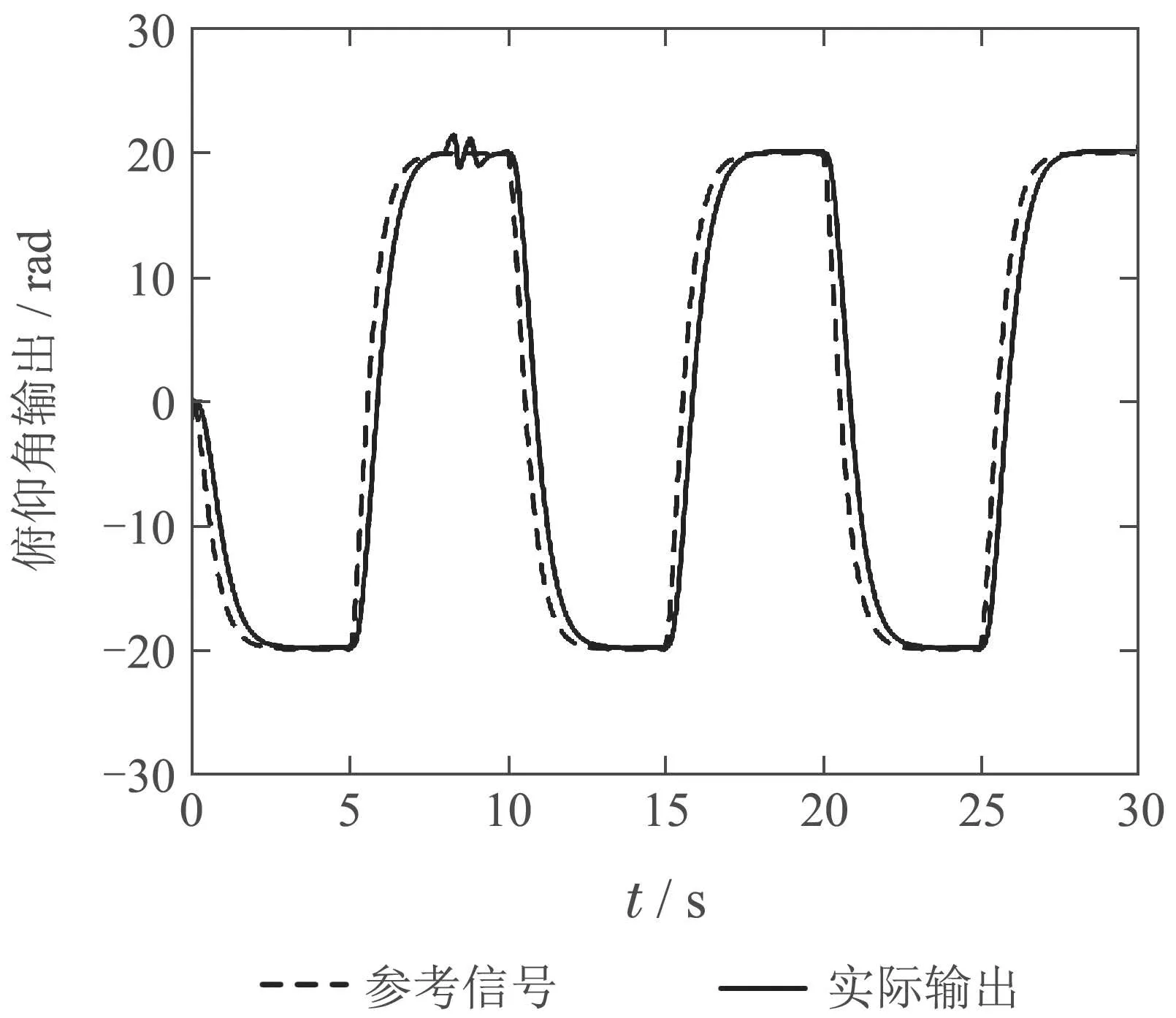
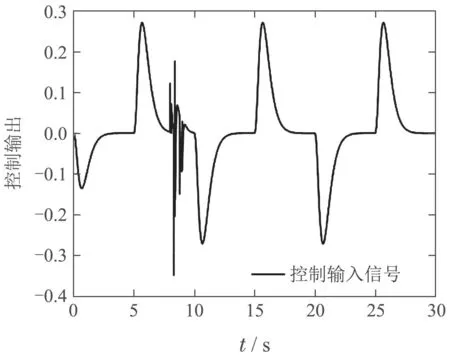
图12 数字仿真容错过程控制系统容错效果和反馈输出变化(传感器故障)Fig.12 Fault-tolerant effects and feedback output changes of digital simulation fault-tolerant process control systems(sensor failure)

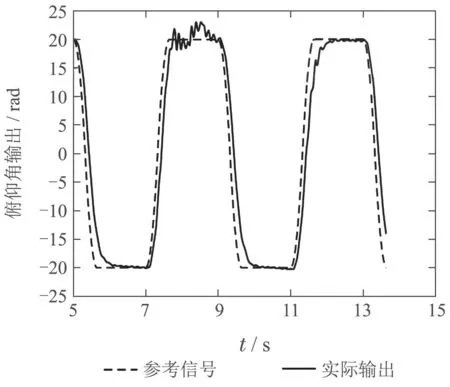
图13 物理平台传感器故障容错俯仰角输出Fig.13 Pitch angle output during fault tolerance of physical platform sensors

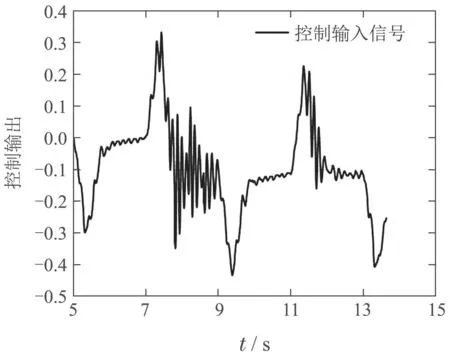
图14 物理平台容错控制反馈输出Fig.14 Control feedback output in the physical platform fault tolerance process

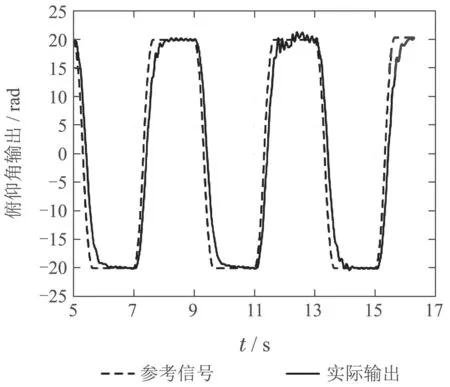
图15 传统强化学习方法下传感器故障容错俯仰角输出Fig.15 Pitch angle output in sensor fault tolerant process under traditional reinforcement learning method

6 结论

本文基于强化学习的Q-learning方法,提出了一种主动容错控制方案,并且基于南京航空航天大学“先进飞行器导航、控制与健康管理”工信部重点实验室的飞行器故障诊断实验平台对所提出的方法进行仿真验证.仿真结果表明,本文所提出的增量式策略强化学习容错控制算法,能够在飞行器发生故障时尽可能地保持原有飞行轨迹,完成原定任务,本篇文章主要创新点如下:

1)通过强化学习控制器,采用评价网络对系统产生的实时数据进行特征的提取,从而获取故障信息并基于此做出对系统控制器的调整,相比于传统的基于模型的容错控制方法,此方法是一种基于数据的主动容错控制方法,突破了复杂系统建模困难的局限,并且通过对数据特征的提取替代了故障检测子系统,简化了控制器的设计;

2)对于不确定性故障的前提,提出了增量型策略的强化学习控制器,改进了传统强化学习算法中采用确定性的固定策略的局限,从而实现对当前所产生故障系统的最优容错策略的逼近;

3)通过状态转移预测网络进行下一步状态的预估,实现了连续控制系统的实时策略网络的更新.