主奇异子空间跟踪算法与性能分析
杜柏阳 ,孔祥玉 ,冯晓伟
(1.火箭军工程大学导弹工程学院,陕西西安 710025; 2.火箭军工程大学核工程学院,陕西西安 710025)
1 引言
在现代信号处理中,许多问题可以转化协相关矩阵的分解问题,从而通过奇异值分解的方法最终有效地解决[1].奇异特征空间提取方法广泛应用于信息产业等领域,例如低秩优化[2]、人脸识别[3]、功耗分析[4]、故障诊断[5]、波达角估计[6]等.通常,主奇异特征向量(principal singular component,PSC)指的是在由两路输入信号得来的协相关矩阵中,与几个主要奇异值对应的特征向量,该向量是成对存在的,区分为左和右两个向量.由这些特征向量张成的空间称为主奇异特征子空间(principal singular subspace,PSS).
实现奇异特征提取的最初方法主要依赖矩阵分解理论[7–8],基于矩阵分解的处理算法具有良好的鲁棒性,但他们是批处理算法,只能处理离线数据,因而该类方法计算效率很是受限,而且对硬件设备要求比较高.神经网络算法具有在线学习的特点,能够实现奇异特征的在线提取,因而被广泛开展研究,例如Hebbian规则算法[9–10].早期的神经网络算法需要将协相关矩阵R改造成RTR或者RRT.这种做法确保了被分解矩阵的对称性,但是还存在秩缺失情况下的算法稳定性问题[11],这在实际应用中是不可避免的.针对这个问题,有学者提出基于梯度的神经网络算法[12–14],降低了对协相关矩阵的要求.Kung和Diamantaras[13]提出了互相关神经网络(cross-correlation neural network,CNN)模型,该模型可以直接从高维信息流中提取互相关特征.然而,这一类算法能提取信号特征中与最大的奇异值相对应的一对奇异成分,还没有考虑在信号中提取奇异特征子空间的问题.目前,针对奇异特征子空间提取方法的研究亟待进行.
通常来讲,诸如Hebbian类的神经网络算法大多是通过优化信息准则的方式获得的[15].信息准则包含算法的优化目标,由梯度下降法、牛顿法等不同方法进行推导,可得到相应的特征提取算法.优化方式不同,对应的算法也不尽相同.因而信息准则对于优化算法的搜索方向,提高算法的自稳定性,以及扩展算法的形式等具有十分重要的意义.Feng等[16]在Kung等[13]的CNN模型基础上,设计了新的优化框架,并给出了一个信息准则
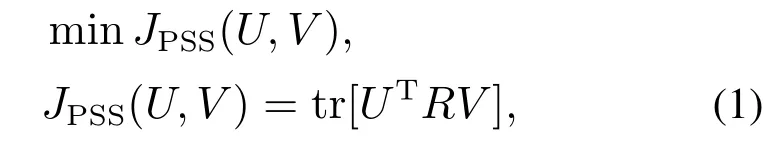
其中: U ∈RM×r和V ∈RN×r分别为左右奇异特征向量张成的奇异子空间,当r1时,U和V 退化为单个主奇异特征向量.该信息准则表达了算法优化目标的核心内容,即寻找能够使矩阵UTRV 的秩最小的左右奇异子空间.该信息准则的提出对于后来学者[17–18]的研究工作具有一定的启发意义.一方面,该信息准则本身体现了从信息角度对奇异特征信息提取过程的物理意义;另一方面,该信息准则为后续信息准则在数学和物理两种意义上的延伸提供了借鉴和参考的依据,可以丰富算法的功能,提高算法在工程中的应用价值.
众所周知,在实际工程应用中,收敛性和自稳定性是神经网络算法十分重要的性质.收敛性是算法最基本的性能,这里不做赘述.自稳定性是指算法不限定于特定的初始设定值,在信息变化较大的情况下,算法依然保持收敛的性质.Kong等[17]分析Kung等[13]的算法表明,该算法在某些情况下不具有自稳定性,特别是当协相关矩阵接近奇异状态的时候.这在一定程度上降低了Kung算法在实际应用中的价值.
在本文中,针对输入信号奇异特征的在线提取问题,作者提出一种新的信息准则,采用梯度下降法推导出对应的奇异子空间提取算法.通过李雅普诺夫函数方法对提出的算法进行收敛性分析,求解算法实现收敛的基本条件.通过常微分方程(ordinary differential equation,ODE)方法对提出的算法进行自稳定分析,求解算法实现自稳定的基本条件.最后通过MATLAB仿真验证算法的理论分析结果,检验算法的性能,为该算法在实际生产生活中的应用奠定了良好的基础.
2 信息准则和算法的提出
对于一个N维数据序列{y(k)}和M维数据序列{x(k)},定义其协相关矩阵为RxvE[y(k)xT(k)].根据该定义,获取协相关矩阵必定要求遍历全部输入信号,而这对在线的信号处理过程是无法实现的.为实现算法在线提取信号特征,需要通过在线估计的方式求得信号的协相关矩阵[19].估计的方式大体分为两种情况.如果两个数据序列同为平稳序列,那么它们的协相关矩阵可以估计为

其中R(k)为第k次迭代中协相关矩阵的估计.当两个数据序列任一个是缓变序列时,它们的协相关矩阵被估计为

其中α为遗忘因子,通过遗忘因子可以保证过去输入的权重总是小于最近输入的权重.一般来说,α ∈(0,1)其具体取值需要依赖于信号的性质,缓变序列的变化越缓慢的系统α的取值越接近1,反之则越接近0.相比而言,第2种估计方式相比于第1种估计方式,更加重视邻近迭代中的信号信息.
对一个矩阵特征值分解,可以分为两个部分[1]:
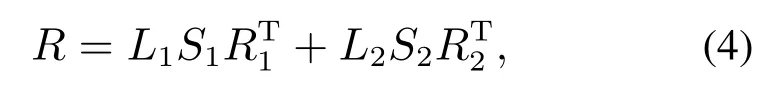
其中:L1[l1l2··· lr]∈RM×r和R1[r1r2···rr]∈RN×r分别为左右主奇异特征向量张成的PSS,奇异特征值则由矩阵S1diag{σ1,σ2,···,σr}∈Rr×r对角线上各个元素表示.本文仅讨论主奇异值为正的情况.是最小均方误差意义下对R阵的r秩估计,是R阵的主要成分,r小于等于M和N中的较小者.表示R矩阵SV D的次要成分,其中L2[lr+1lr+2··· lM]∈RM×(M−r), R2[rr+1rr+2··· rN]∈RN×(N−r).另外,IminM,N−r都是正交矩阵.
构造一个新型的信息准则如下:
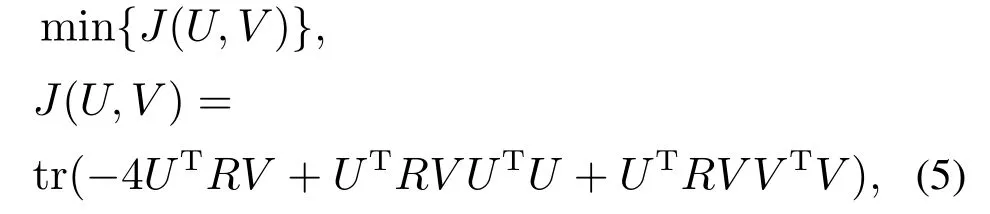
对该信息准则细节分析通过两个定理[1]给出.
定理1L1和R1为R的左右主奇异特征矩阵,Λ为奇异值矩阵为S1,则存在旋转矩阵QU和QV,使J(U,V)处于平衡状态,其中:QU
证 J(U,V)存在平衡状态的充分必要条件是存在U和V,使J(U,V)对U的偏导数和对V 的偏导数0同时成立,于是有
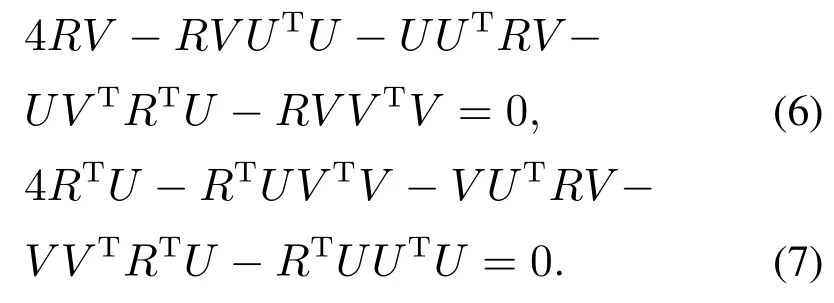
对式(6)等号两边同时左乘UT,对式(7)等号两边同时左乘VT,可得
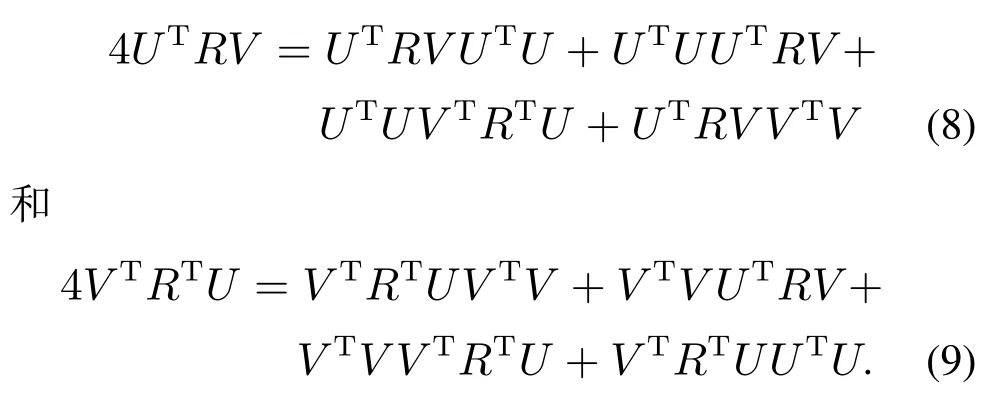
式(8)与式(9)相加,并化简可得

再由UTRV(VTRTU)T,将式(9)等式两边同时转置,再与式(8)相减可得

考虑到式(10)–(11)对任意J(U,V)和R都成立,则设U[u1u2··· ur], V[v1v2··· vr],代入式(10)–(11)中,可得方程组
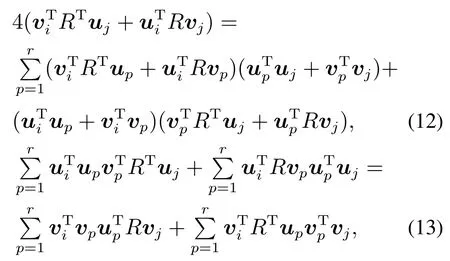
对式(12)分析可得

对式(13)分析可得
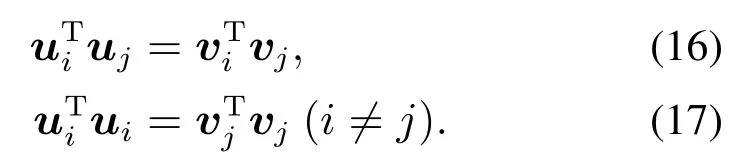
联立式(14)–(17),可得U和V 均为单位正交矩阵.再结合式(6)–(7)可得
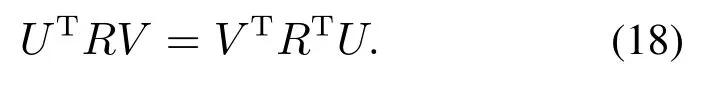
已知L1和R1为左右奇异矩阵,S1为奇异值矩阵,则U和V 在L1和R1空间的投影分别为QU.由

可得QU和QV为旋转矩阵.
下面进行充分性证明,已知U和V 均为单位正交矩阵,UTRVVTRTU,代入式0 和0,并化简可得


由rank(L1)rank(R1)r,J(U,V)仅与前r个成分相关,可知式(23)–(24)的解空间维度均为0,因而0 成立.证毕.
注1本文算法主要适用于实数域的信号,或者经过转化最终在实数域对信号进行处理,因而J(U,V)规定QU和QV的取值空间为{(QU,QV)|ΛQV>0}.
定理2当且仅当UL1QU, VR1QV, QU和QV为旋转矩阵时,J(U,V)全局极小,极小值为−2tr(S1). QU和QV为非旋转矩阵时的平衡点均为J(U,V)的鞍点.
证由式(5)容易看出,当→∞或者→∞时,J(U,V)也是趋向于无穷大的.因而J(U,V)是一个有下界而无上界的函数.根据文献[21],函数的极值可通过计算Hessian矩阵判断.

由于计算过程复杂,计算步骤相似,本文主要说明式(25)的推导过程.由UL1QU, VR1QV可知
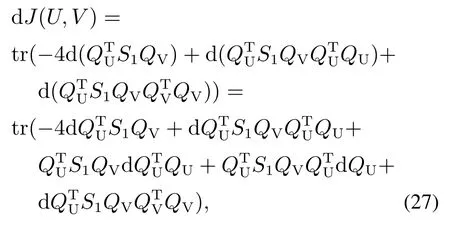
然后,二阶微分为

那么,可得
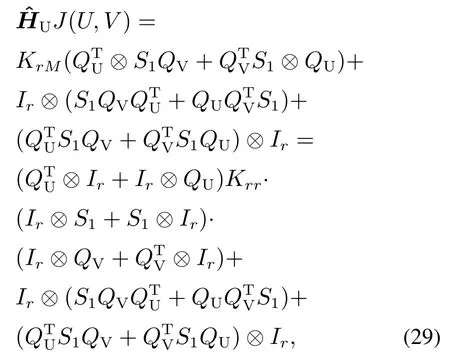
其中: ⊗表示直积运算;Krr表示一个r2×r2的置换矩阵,;式(29)是通过如下公式计算而来的:
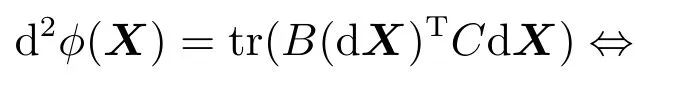

其中: ϕ(X)为被二阶微分的函数,X ∈Rp×q.分析式(29)可知等式右边的3项式子均为对角线矩阵,由QU和QV为旋转矩阵可知对角线矩阵分别为Ir⊗S1+S1⊗I,2Ir⊗S1和2S1⊗Ir.(U,V)矩阵的对角线元素均大于零,那么J(U,V)为正定函数.由此得证,UL1QU,VR1QV就是J(U,V)全局极小点.将UL1QU,VR1QV代入式(5)可得该处的值为−2tr(S1).
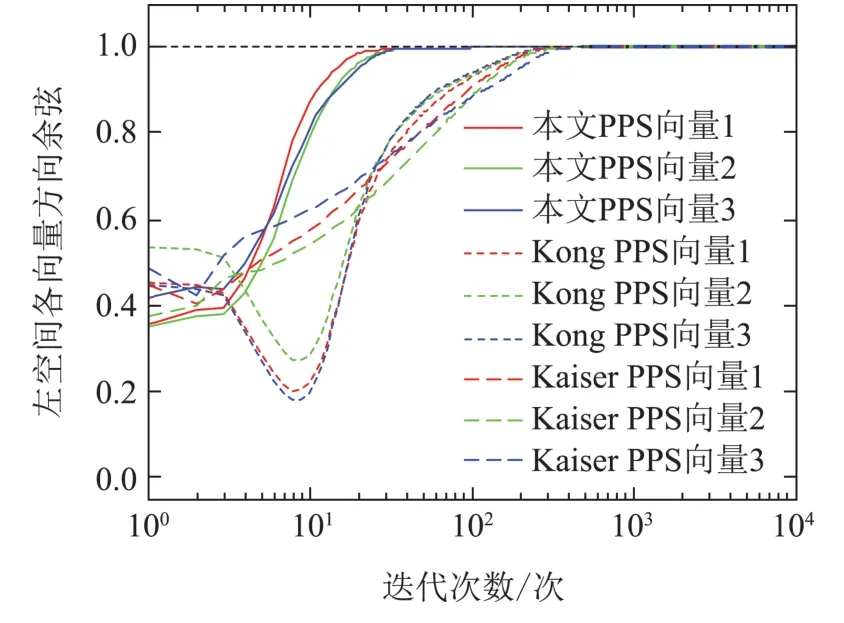
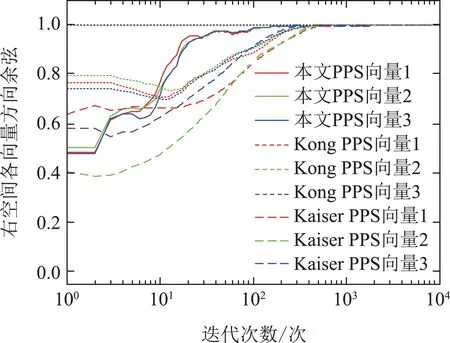
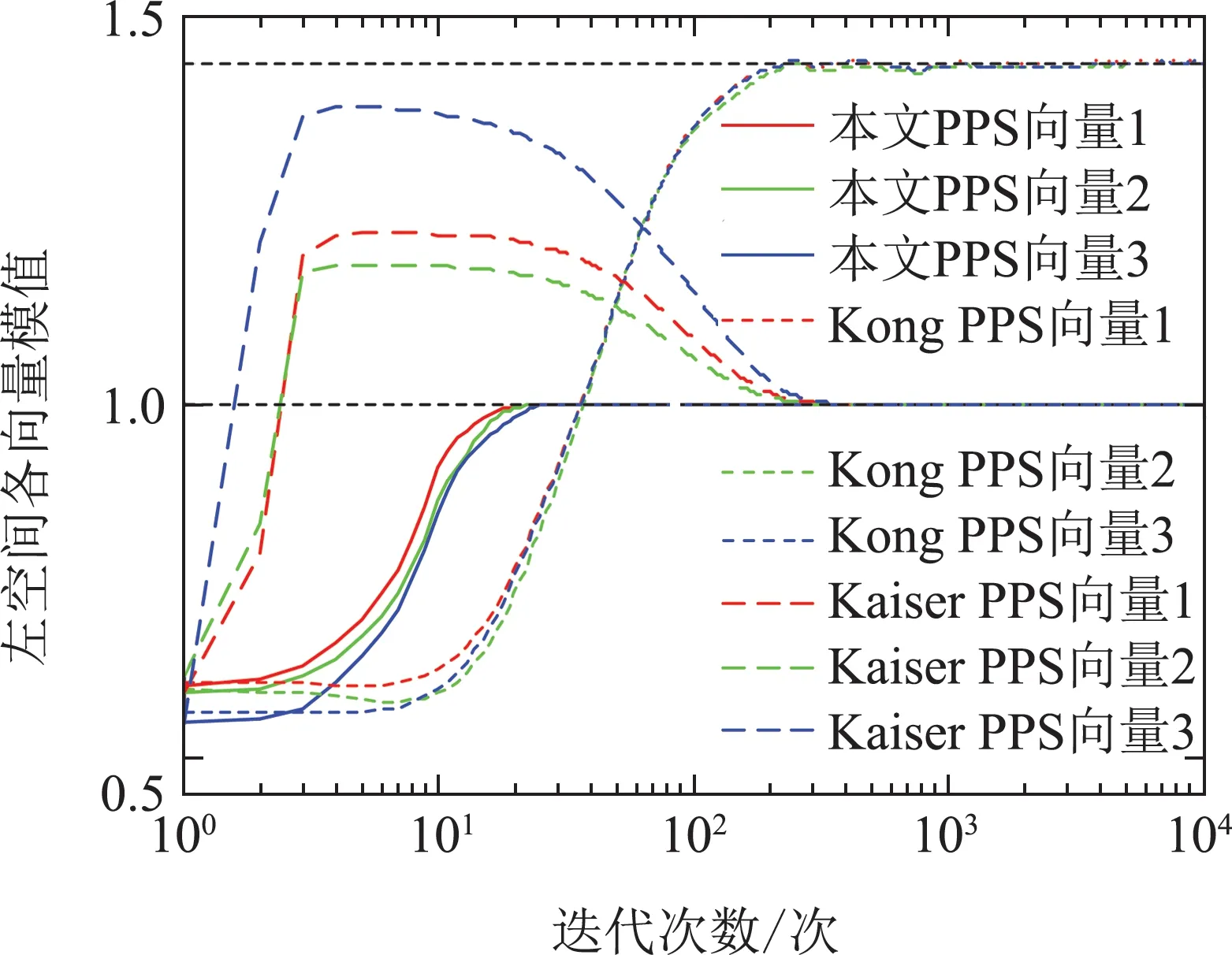
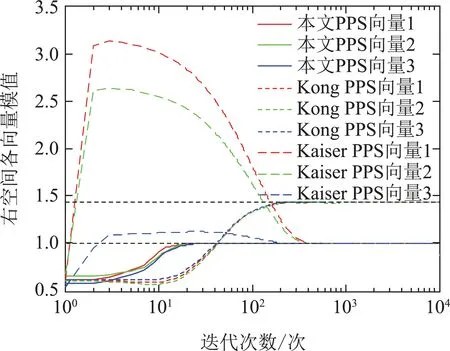
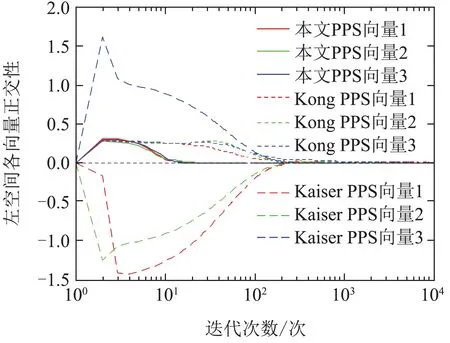
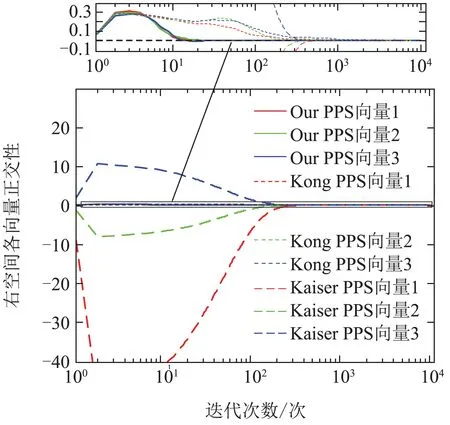
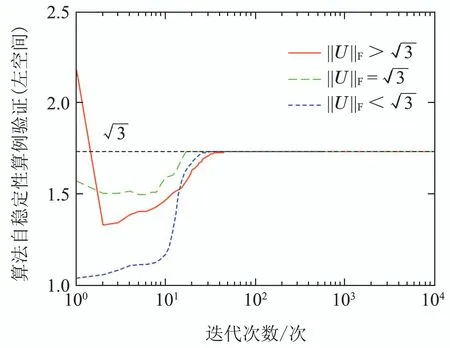
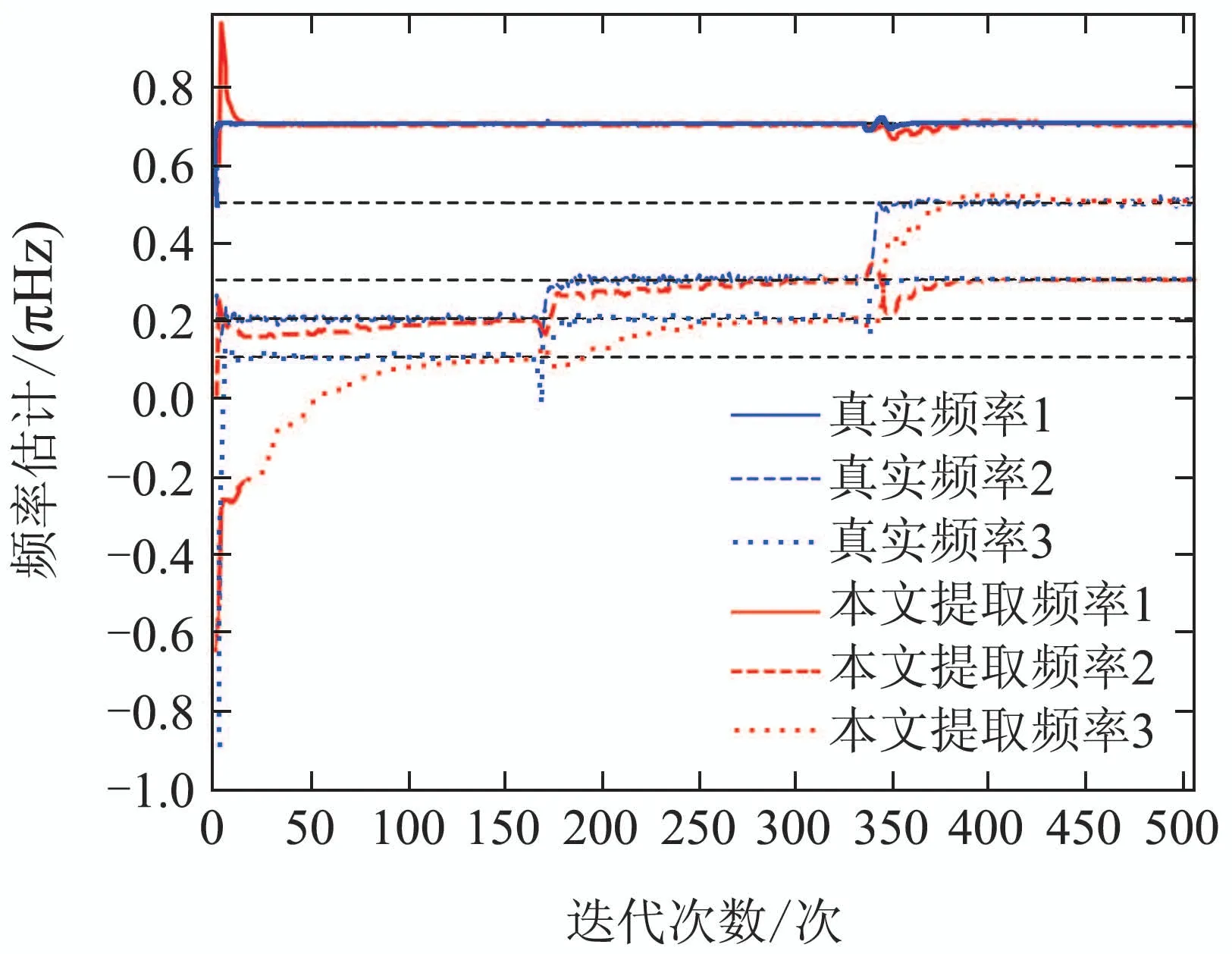
下面证明其他平衡点均为鞍点.判断一个平衡点为鞍点的标准[14]是在平衡点无限小的邻域内存在一点(U′,V′),使J(U′,V′) 注2通过分析定理2可知,信息准则只有全局极值点而不存在局部极小点,由此可得,该信息准则的梯度下降搜索算法总能够全局收敛到期望的主奇异子空间. 下面采用梯度下降法求解单层神经网络算法. 分别对U和V 对信息准则J(U,V)求梯度可得 该梯度函数可以理解为信息准则在(U,V)的动力学系统,按照梯度下降法[22]的基本思路,认为此时算法的梯度即为U 和V 的更新方向,即为∇UJ(U,V)−∆U和∇VJ(U,V)−∆V,于是可知自适应算法如下: 其中学习因子η ∈(0,1),U(k)和V(k)为k时刻的状态向量.特别注意的是,当r1时,矩阵U和V 就退化为两个状态向量u ∈RM×1和v ∈RN×1,算法可以实现单个主奇异特征向量的提取, 这个算法可以适用于一些应用中仅需要提取最大的奇异特征向量的情况. 本文考察算法的性能主要从收敛性和自稳定性两个角度分别展开.收敛性是算法能够完成基本提取任务所必须具备的性能,收敛性能的优劣对算法质量评价具有决定性意义.本文主要采用李雅普诺夫方法对收敛性展开分析,从而得到理论结果.自稳定性也是算法非常重要的性质.算法如果仅在特定初始条件以及限定的干扰条件下具备良好的收敛性能,那么它的应用范围会受到很大的限制.具备良好的自稳定性的算法相比不具有该性能的算法拥有更高的应用价值.本文通过ODE方法,开展对算法自稳定性的分析. 对式(40)–(41)进行分析可知,在学习因子足够小的情况下,该式可以通过一个连续时间的常微分方程来近似[23]: 算法(40)–(41)的收敛性条件等价于式(44)–(45)的全局收敛条件,因此考虑采用李雅普诺夫理论分析式(44)–(45)的全局收敛性.显然,信息准则J(U,V)是有下界的,连续而且还是连续可微的,满足作为常微分公式李雅普诺夫函数的条件.具体条件通过定理3分析可得. 定理3考虑初始状态(U0,V0),如果学习因子足够小,并且状态向量(U(t),V(t))满足ODE约束,那么当时间t →∞时,状态向量以概率1收敛到固定点(L1QU,R1QV). 证根据式(5)可设计一个能量函数 研究该式可以发现,当t →∞时,∥U∥F和∥V ∥F有上界,此时E(U,V)存在上界,那么对应的自变量(U,V)就存在一个有界的定义域.容易知道,E(U,V)是连续函数,而且是一阶微分连续函数.那么,对E(U,V)求梯度可得 由此,根据微分矩阵的链式规则[24],可以求解E(U,V)的微分 证毕. 注3收敛性分析的内容结合了前期对信息准则的分析结论,这表明李雅普诺夫意义下的能量函数,在一定程度上同表达信息分布的信息准则在信息论分析的角度具有相关性. 自稳定性是指算法迭代过程中,以任意初始值开始,状态向量总是能够移动到一个特定的点,其具体表现是状态向量的模值总是收敛到一个固定值.有学者[25]通过研究多个算法的稳定发现,缺乏自稳定性能的算法是潜在发散的,因此对自稳定性能的分析十分必要.根据范数理论状态向量U的自稳定性按照F范数意义下的稳定性展开分析. 定理4在学习因子足够小,输入的向量有界,并且初始状态模量存在上界2r的情况下,在算法(40)–(41)中,U和V 的F范数总能够收敛到常数1. 证首先求解U(k+1)和V(k+1)的F范数,根据式(40)–(41)可知 其中考虑到学习因子足够小,高阶项o(η2)对范数影响在后续的研究中可以被忽略.由此可知 经过式(50)中关于矩阵的迹的一些数学计算和推导,可得∥U(k)两步之间模值关系的几种不同的情况: 该式表明,状态向量的模值比例情况可分为如下3种:当∥U(k)<2r时,算法状态向量的模值在本次更新过程中会增大,而且在∥U(k)>2r时会减小,最终的趋势是状态向量的模值∥U(k)能够逐渐稳定在常数2r附近.这表明,提出的算法的收敛性能不依赖于状态向量之前的数值,在协方差稳定的情况下总是使得状态向量向着确定的方向收敛.这表明该算法具有自稳定性.证毕. 仿真实验主要从3个角度展开,首先从状态矩阵的模值和方向余弦两个方面体现所提出算法的收敛性;其次验证算法的自稳定性;最后通过所提出算法在高维波束频率估计的应用,展示该算法在实际应用算例中的性能.在算例1和算例2中,蒙特卡洛仿真次数为40,实验的结果就是这40次独立运行结果的平均. 其中: ui和vi(i0,1,···,4)分别为一个七维和五维的正交离散余弦基函数;A0是一个对角矩阵,从上到下分别为10,10,10,2,10−2.理论上,通过式(53)计算出来的协方差矩阵,其奇异值就等于A0矩阵对角线上的各个元素.设置三重根10,并且条件数为104,此时协方差矩阵是病态的.并且所提取的奇异子空间对应信号前3个主奇异特征成分所张成的子空间.另外根据定理约束,确定学习因子η0.1,状态向量的初始值U0和V0都是随机生成的,其中每一个列向量的模值均为1.本文通过对比所提出算法,Kong算法[17]和Kaiser算法[20]体现出所提出算法在收敛速度、收敛精度等方面的优良性能. 为清晰地描述算法的收敛速度和精度,分别从方向和长度两个方面定义状态矩阵的方向余弦和模值长度.一般而言,状态矩阵最终收敛到的子空间总是与前3个主奇异特征向量张成的子空间存在一个旋转矩阵的相位差,因此定义Ulss[u1lssu2lssu3lss]在k时刻的方向余弦为 其中lj和rj分别为协方差矩阵的真实的左右奇异成分.这样无需预先计算旋转关系矩阵,就可以验证两个子空间等价.另外,子空间的模值长度通过状态向量的2范数估计 为了更清晰的展现子空间的空间特性,考察子空间正交性,定义向量的正交积为 去掉重复的计算,分别计第1个值为第一、二向量的正交积,第2个值为第二、三向量的正交积,第3个值为第一、三向量的正交积. 如图1所示,在左空间中,本文所提出算法的方向余弦变化情况用实线表示,Kong算法的余弦变化情况用虚线表示,Kaiser算法的余弦变化情况用段线表示,与前3个最大奇异特征值相对应的3个特征向量分别用红绿蓝3种颜色标示.容易看出,3种算法的3条线都是逐渐收敛到1的位置,这表明算法能够在方向上跟踪得到输入信号的左奇异特征子空间.3种算法中,本文提出的算法明显需要最少的迭代步数,并且算法到达1以后,存在最小的波动变化.右空间的分析与此相似.这验证了理论分析的结果. 图1(a) 左奇异子空间的方向余弦收敛过程Fig.1(a) Direction cosine convergence of the left principal singular subspace 图1(b) 右奇异子空间的方向余弦收敛过程Fig.1(b) Direction cosine convergence of the right principal singular subspace 图2展示的是各个算法模值变化的情况,各种线条对应的算法以及向量与图1相同,以左空间为例,本文所提出算法的模值变化情况用实线表示,Kong算法的模值变化情况用虚线表示,Kaiser算法的余弦变化情况用段线表示,3个向量分别用红绿蓝3种颜色标示.图中显示,3种算法不同向量的曲线都是逐渐收敛到一个固定的实数值的位置,其中,本文提出算法和Kaiser算法都是收敛到1的,Kong算法的曲线则收敛到1.44附近.显然,本文算法的各个曲线都是以最少的迭代次数收敛到稳定状态的,这体现了本文提出算法在收敛速度方面的优越性.另外,本文提出算法的曲线在收敛到1以后,几乎看不到任何波动的迹象,而Kong算法和Kaiser算法在收敛到稳定状态的初期存在一定的波动.这又说明了本文提出算法在收敛精度方面的优势.对右空间的分析也能够得到相似的结论. 图3中,以左空间为例,本文所提出算法的正交积的变化情况用实线表示,Kong算法的正交积的变化情况用虚线表示,Kaiser算法的正交积变化情况用段线表示,3个向量分别用红绿蓝3种颜色标示.3种算法的各条曲线均不为零则表明3条向量存在不相互垂直的部分,经过短期震荡后,3条线均收敛到零值,此时各个向量完全正交,并一直保持到最后.右空间的分析与此相似.但是需要指出的是,图3(b)中由于Kaiser算法的曲线变化幅值较大,故将图中−0.1 ∼0.4的部分放大,用来显示本文算法和Kong算法的曲线变化情况. 图2(a) 左奇异子空间的模值长度收敛过程Fig.2(a) Norm convergence of the left principal singular subspace 图2(b) 右奇异子空间的模值长度收敛过程Fig.2(b) Norm convergence of the right principal singular subspace 图3(a) 左奇异子空间的各向量正交积曲Fig.3(a) Orthogonality of each vector in the left principal singular subspace 图3(b) 右奇异子空间的各向量正交积曲线Fig.3(b) Orthogonality of each vector in the right principal singular subspace 另外,本文还比较了算法的计算复杂性.本文提出算法的计算复杂度每次更新分别需MNr+5Mr2+Nr2和MNr+5Nr2+Mr2个浮点计算.Kong算法的计算复杂度为每次更新分别需MNr+4Mr2+Nr+Mr和MNr+4Nr2+Nr+Mr个浮点运算.Kaiser算法的计算复杂度每次更新均需要2MNr+Mr2+Nr2个浮点运算. 与第4.1节算例1相似,本算例的输入序列x(k)和y(k)均为高斯白噪声序列,并同样将他们的关系设置为y(k)Ax(k),并且A值保持不变.不同之处是本算例研究目的着重在初始状态矩阵的模值,算法对收敛性的保持状态.因此,设置3种不同情况展开验证.具体而言,首先随机生成一组向量作为状态向量的初始值U(0)和V(0),然后将该向量的范数规范为2.2,1.7和1.0,分别对应大于、等于以及小于√这3种情况,最后分别验证这样的设置下算法状态矩阵的F范数变化情况.其中,状态矩阵的列数r3,根据定理4可知,F范数最终稳定在√处.另外,根据定理约束,确定学习因子η0.1. 算法自稳定性的仿真结果如图4所示.图4(a)和4(b)分别表示左和右奇异子空间的变化情况,3种初始条件的变化曲线分别用实线、虚线和点线表示.在左空间中,不同模值的初始状态使3条曲线起始于完全不同的3个位置,但是在无论哪一种初始条件情况下,算法总是最终稳定在√这同一条曲线上. 由此,可以说明该算法具有良好的自稳定性.另外,状态空间收敛到稳定状态的迭代次数也是十分接近,这一方面呼应了算例1中的算法迭代次数,另一方面也体现出了算法收敛的行为具有相似性.右空间的变化情况与左空间类似,在左空间中相应的结论也适用于右空间. 图4(b) 算法自稳定性数值验证(右空间)Fig.4(b) Self-stabilizing property verification in the right principal singular subspace 本算例是验证提出方法在高维波束跟踪问题中的应用效果.设置高维波束存在3个阶段的变化,阶段之间的变化是突然的,每个阶段都存在3个频率,具体的波束函数如下设置. 其中:n(k)∈[−0.5,0.5]表示白噪声,τ是噪声信号的系数.有兴趣的读者可通过文献[1]了解关于该波函数的详细知识.高维波束频率分析问题可以通过提取两个数据流的主奇异成分获得.这两个数据流可以构造为 其中:K为样本总数,M为x数据流的维度数,N为y数据流的维度数. 图5展示出了算法在频率的跟踪速度和估计精度两个方面的性能.图中蓝色虚曲线表示通过奇异值分解,红色实曲线表示本文算法跟踪的子空间方法对频率的估计.从算法曲线在不同阶段间的表现来看,算法能够在150次迭代中成功跟踪发生激烈变化的频率,体现了跟踪算法的快速性.算法在每后半阶段中,震荡幅度逐渐减小,最终与奇异值分解方法的曲线高度重合,这体现了算法具有较高的估计精度.总之,本文提出算法在高维波束频率估计问题中有良好的效果. 图5 本文算法在频率估计中的变化曲线Fig.5 Evolution curves of the proposed algorithm for estimating the frequencies 本文提出了一种新型的主奇异子空间跟踪算法.首先提出一种新的信息准则,理论分析了信息准则极值点的存在性和唯一性.然后基于提出的信息准则,通过梯度下降法推导出一种神经网络搜索算法,实现了对输入信号主奇异子空间的跟踪.算法的收敛性和自稳定性分别通过李雅普诺夫函数方法和ODE方法进行了分析.最后,不同形式的MATLAB仿真验证实验表明,该算法具有较快的收敛速度,较高的收敛精度以及良好的自稳定性能.因此,提出算法具有较高的实际应用价值.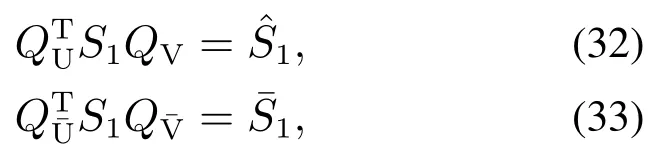


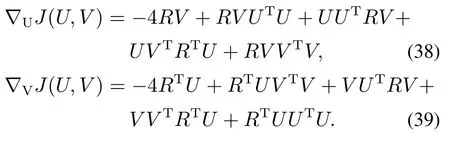
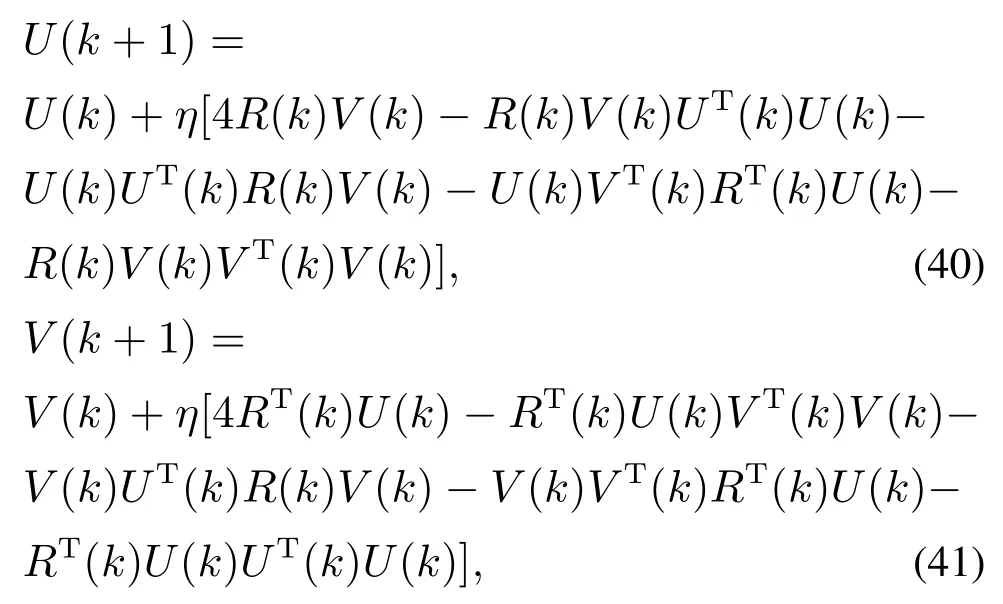
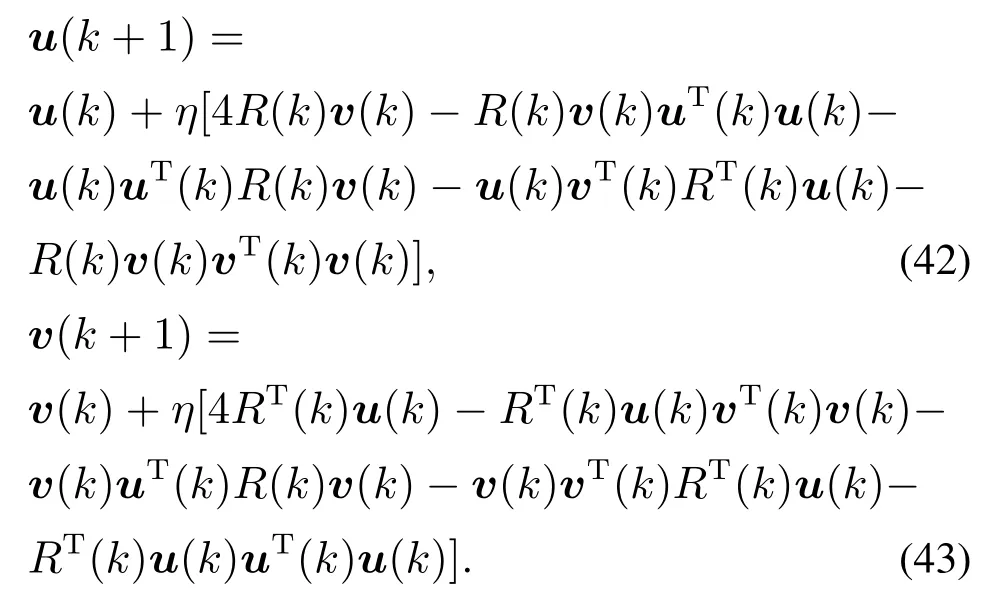
3 算法的性能分析
3.1 算法收敛性分析

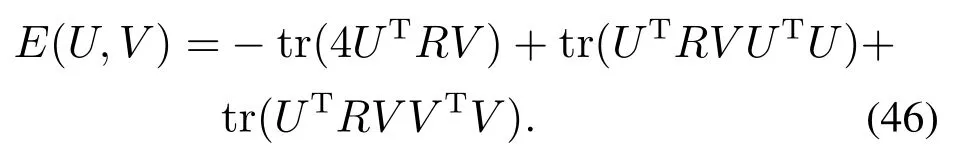
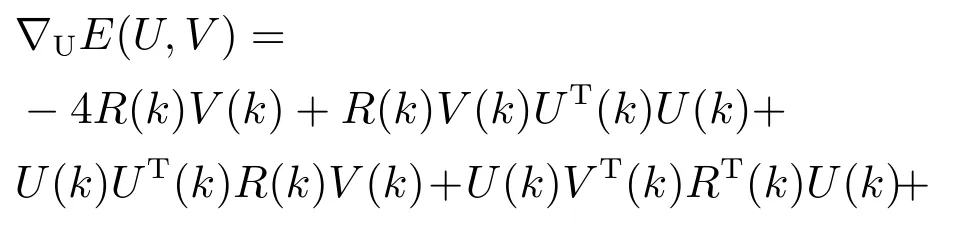


3.2 算法自稳定性分析
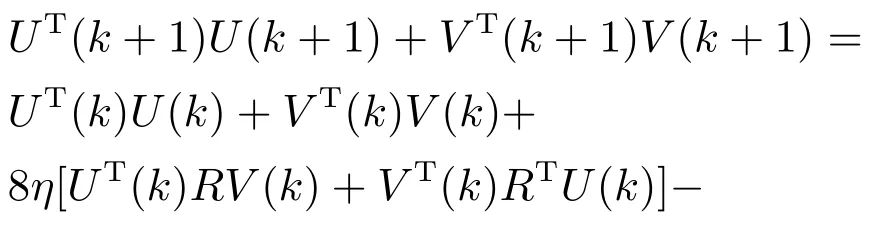

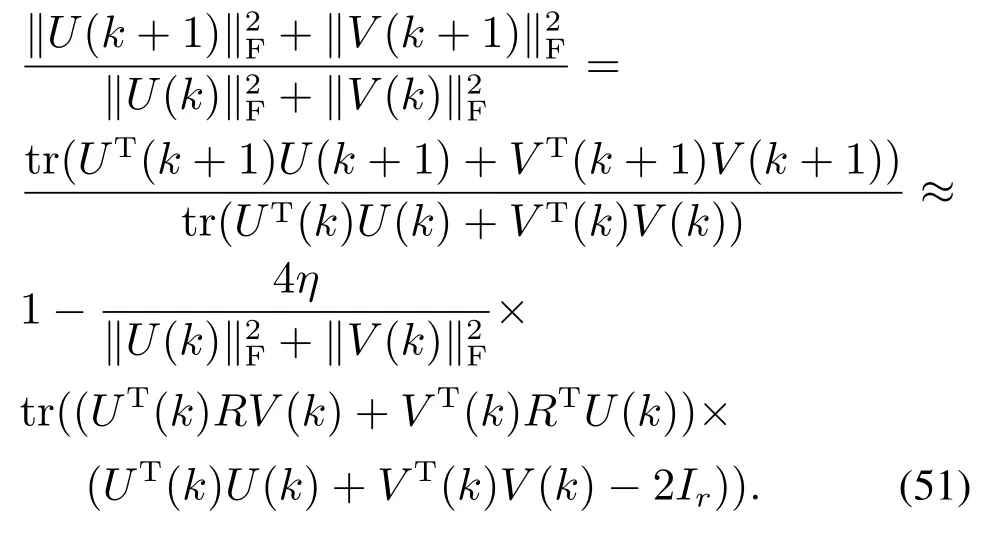

4 仿真实验
4.1 算例1:算法收敛性验证

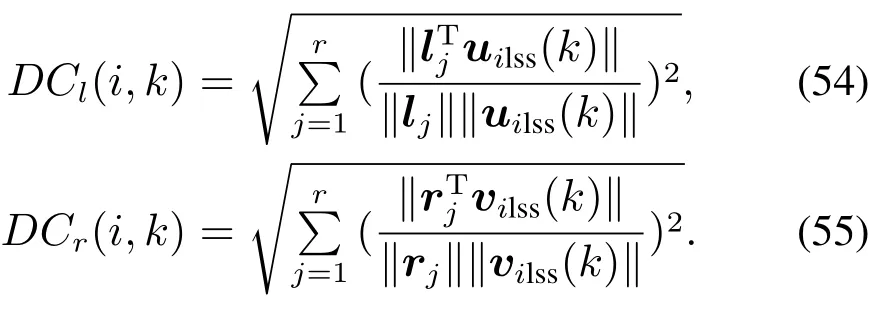


4.2 算例2:算法自稳定性
4.3 算例3:本文算法在高维波束频率分析中的应用
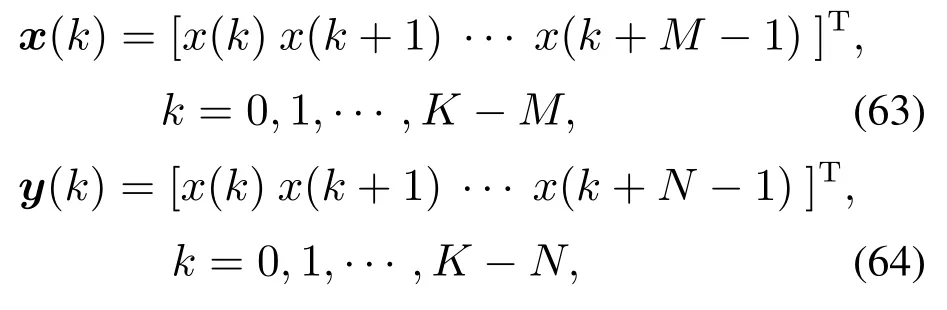
5 结论

