考虑测量不确定和输入饱和的充液航天器自适应鲁棒控制

王宏伟,吕书锋,宋晓娟

(1.内蒙古工业大学机械工程学院,内蒙古呼和浩特市 010051;2.内蒙古工业大学理学院,内蒙古呼和浩特市 010051)

1 引言

现代航天器通常携带大量的液体燃料用于支撑自身机体完成复杂的航天器任务,例如任务侦查、深空探测.完成一系列复杂的航天任务需对航天器姿态反复调整,在航天器进行姿态运动时,贮箱内液体不可避免的会发生晃动,进而影响航天器姿态运动的稳定性[1–3].液体晃动不但对航天器自身的姿态运动产生很大的影响,而且对充液航天器的控制器设计带来极大的挑战.一方面,充液航天器是一个欠驱动的系统,这主要体现在晃动燃料位于贮箱内部,很难对其直接施加控制力及力矩;另一方面,航天器运行的空间环境较为复杂,受到多种载荷的作用,例如重力梯度力矩、气动力矩、辐射力矩等,此外,由于航天器的惯性矩阵存在不确定性,这为充液航天器高性能姿态控制器的设计带来了困难.

研究充液航天器的耦合系统动力学模型和稳定性分析是很必要的.在充液航天器建模过程中,多将晃动液体等效为球摆模型和弹簧−质量模型.文献[4]将液体晃动等效为球摆模型推导出航天器数学模型,设计了基于动态逆和输入成型技术相结合的混合控制方法.文献[5]针对液体燃料晃动耗散效应及挠性附件扭转的情况,将液体晃动等效为球摆模型,采用迈尔尼科夫法研究了从短轴到长轴自转姿态过渡机动的混沌动力学问题.文献[6]利用等效球摆模型推导了充液航天器的耦合动力学数学模型,验证了球摆模型与弹簧质量模型的相似性,指出液体晃动具有强耦合和欠驱动的特性.文献[7–9]均将带有部分充液贮箱航天器的晃动质量等效为球摆模型推导出数学模型,研究了自旋航天器控制稳定性问题.

对于航天器姿态控制方面,一些学者在控制器设计中考虑了一些实际条件,例如外部环境干扰[10]、参数不确定[11]、控制输入饱和[10,12]、无角速度反馈[13–14]、有限时间收敛[15–16]等问题.但是测量不确定问题往往被设计者忽略掉.由于姿态测量的环境条件受到较大外部环境的干扰,测量装置无法获得准确的姿态和角速度,因此姿态控制器的设计中通常涉及到测量的不确定性.为了保证闭环系统的稳定性和鲁棒性,应设计一种有效的姿态稳定控制器,以同时处理外部干扰,参数不确定性、控制输入饱和以及测量不确定性.一般来说,控制输入饱和可以通过使用稳定的辅助设计系统直接处理,例如抗饱和补偿器[17–18]、前馈神经网络补偿器[19–20]、指令滤波器[21–22]等补偿输入饱和的不利影响.此外,通过适当的模型变换,可以将外部干扰,参数不确定性和测量不确定性视为集总干扰.干扰观测器技术[23–25]作为一种典型的鲁棒自适应控制方法,已经应用于航天器控制系统中处理系统模型中的集总干扰.然而,在上述研究中,在干扰观测器设计中并未明确考虑测量不确定性的影响.文献[26]针对刚体航天器存在外部未知干扰,参数不确定,测量不确定性以及输入饱和等问题,基于反步控制结合非线性干扰观测器和抗饱和技术设计了饱和鲁棒控制律实现刚体航天器姿态稳定.文献[27]针对测量不确定,外部未知干扰和参数不确定,基于反步控制结合有限时间积分滑模扰动观测器实现了挠性航天器姿态稳定.特别需要强调的是,控制输入饱和以及测量不确定性会降低控制系统的动态控制性能和稳态精度.

本文研究了考虑控制输入饱和及测量不确定的充液航天器大角度姿态机动鲁棒控制问题,主要内容包括:1)将液体晃动等效为粘性球摆模型,利用动量矩守恒定律推导出航天器刚−液耦合动力学模型;2)在航天器姿态控制器设计中,将测量不确定性视为失配和匹配的扰动,并设计相应的的非线性扰动观测器对这些未知的集总扰动进行补偿;3)针对控制输入饱和的影响,设计指令滤波器对控制输入饱和进行补偿;4)在设计的控制器作用下,姿态四元数、角速度、非线性干扰观测器和指令滤波器的状态均渐进收敛到零.

2 充液航天器动力学建模

2.1 姿态动力学方程描述

为了避免参数带来的奇异性,本文使用欧拉四元数描述航天器姿态动力学方程:

式中:[q0q]T[q0q1q2q3]T满足约束条件1;航天器角速度矢量ω[ω1ω2ω3]T;G(q)q0I3+q×,q×为叉乘矩阵,定义为

2.2 建立航天器的数学模型

航天器模型如图1所示,O–XY Z坐标系为惯性坐标系,O1–X1Y1Z1坐标系为航天器本体坐标系,O2–X2Y2Z2坐标系为球摆坐标系.

图1 充液航天器系统动力学模型Fig.1 The dynamics model of liquid-filled spacecraft

假设O1为刚体部分的质心,摆球悬挂点为贮箱中心O2,使球摆悬挂点O2位于航天器本体坐标系的O1X1轴上,摆球的摆长为l,摆球质量为mp,摆球相对于O1的位移矢量为rp,O1到O2的位移矢量为r0.假设图中摆球质量的位置为P点,O1和P点连线上的一点C是主刚体和球摆所组成的系统的质心. C到O1的位移矢量为r1,C到P位移矢量为r2.P点相对于摆球悬挂点O2的位移矢量为r,r关于O2的坐标可以表示为

由于摆长长度和贮箱尺寸的限制,摆球运动的自由度是2维,考虑液体晃动为小幅度晃动,所以摆球振动幅度也为小幅度振动,即y,z ≪l,因此有近似关系x ≈−l.则式(2)可以写成

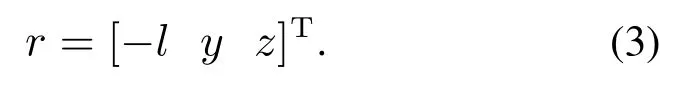
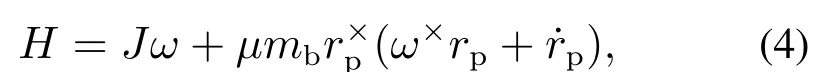
式中:Jb,hp将动量矩守恒定律应用于式(5),产生如下矩阵形式:

推导摆球动力学方程,假设C点在空间中是静止的,球摆关于系统质心C的动力学方程表示为

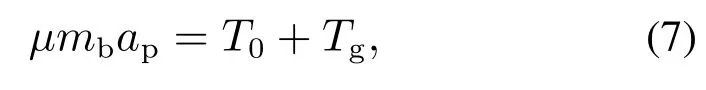
式中: T0−表示球摆所受到的黏性力矩,瑞利耗散函数c1,c2表示燃料黏性系数;Tg表示球摆受到的惯性力矩,U势能函数,g表示航天器惯性加速度的大小.P 点的绝对加速度表示为

由于航天器姿态和角速度是由多个传感器测量的,而传感器通常受到复杂的空间环境的影响,所以其测量值一般是不确定的.因此本文考虑的不确定性包括:航天器上姿态传感器的测量不确定,分别表示为∆q和∆ω,未知的外部干扰d(t)和航天器惯性矩阵的不确定∆J.测量的姿态四元数和角速度表示为

根据式(1)和式(10),可以得到

式中Ξ1

假设1测量不确定∆q和∆ω随时间变化缓慢并且是有界的,也就是说和满足0.因此,∆q ≈0和∆ω ≈0是合理的[28].不考虑其一阶导数及高阶导数对机动系统的影响,即∆q和∆ω以及其高阶导数的影响在机动系统中均可忽略不计.

考虑航天器执行姿态机动,将方程(7)写成矩阵形式,假设液体为小幅度晃动,可将式(6)–(7)做线性化处理,即省略掉方程(6)–(7)中的高阶小量.为了控制系统简述方便,方程(7)引入新的变量ψ,结合方程式(10),测量的航天器动力学方程可表示为如下形式:

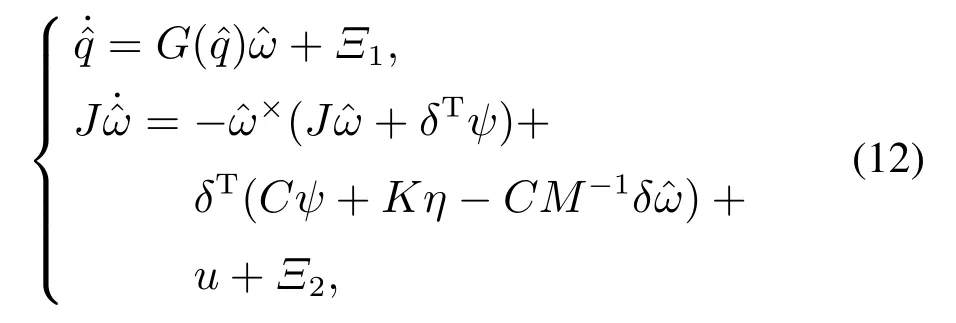
式中:

控制系统中控制力矩存在饱和约束,即|ui(t)|,其中为执行机构提供的最大输出幅值.

3 控制律设计和稳定性分析

针对控制系统模型(12)具有失配不确定性Ξ1和匹配不确定性Ξ2的典型串级结构,将经典的反步技术,非线性干扰观测器和指令滤波相结合,针对航天器控制输入饱和以及传感器测量不确定,设计鲁棒饱和姿态控制器,实现航天器姿态机动的稳定性.

3.1 基于非线性干扰观测器的反步控制

反步法是一种基于递归的Lyapunov的方法.其思想是通过将一些状态变量视为虚拟控制并为它们设计中间控制律来递归地设计控制器,与其他控制方法相比,反步法的优势在于其设计灵活性.

步骤1定义反步变量

式中α ∈R3×1表示虚拟控制律.关于x1的动力学方程可以写成

设计虚拟变量输入为

式中: G−1(x1)是G(x1)的广义逆矩阵,k1是正常数,是Ξ1的估计值.非线性干扰观测器提供了有效的方法估计系统(13)中的失配干扰,设计为

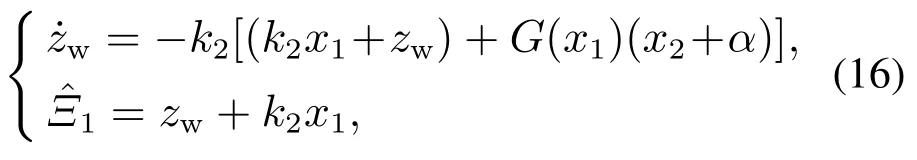
式中:zw为非线性观测器的状态向量,常数k2>0为干扰观测器增益.将式(15)代入式(14)得到闭环系统姿态动力学方程

假设2集总扰动Ξ1随时间变化缓慢且是有界的,这样有∞且满足0.因此是合理的[28].

考虑Lyapunov函数

将其对时间求一阶导数,结合假设2可得

步骤2根据式(12)−(13)和式(15)−(16)可以得到关于x2的动力学方程

针对式(19)中的匹配干扰Ξ3,设计非线性干扰观测器如下:

式中:dw为非线性观测器的状态向量,常数k3>0为干扰观测器增益.

假设3集总扰动是有界的,也就是说这样有ϖ∥x1∥,其中ϖ为正常数.

考虑Lyapunov函数条件

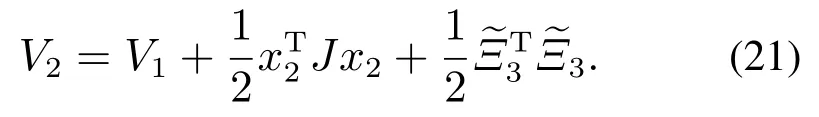
将式(21)对时间求一阶导数,并结合式(16)和式(18)−(20)可得

设计状态反馈反步控制律

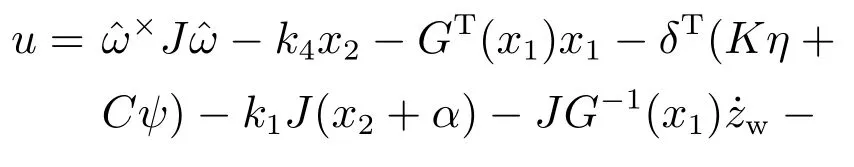
式中k4为正常数.

将式(23)代入式(22)可得

定理1考虑姿态机动控制系统式(12),若设计状态反馈反步控制器式(23),且设计非线性干扰观测器式(16)和式(20),存在外部未知干扰,航天器转动惯量不确定以及传感器测量不确定的情况下,通过选择合适的控制增益,能够保证姿态和角速度渐进稳定.

证 由式(24)可以得到

结合假设3,上式推导中用到了不等式

进一步整理可得

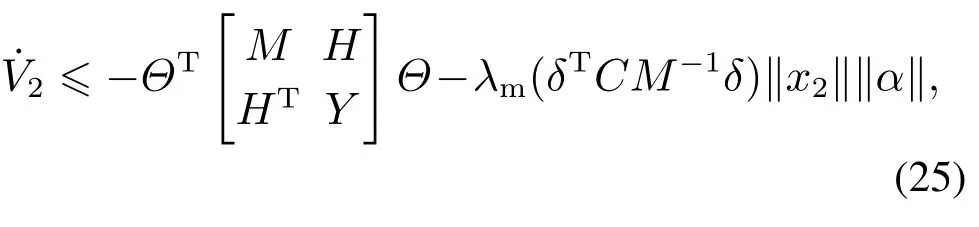
由矩阵的Schur补引理可证明存在足够大的常数k1,k4和足够小的k2和k3,且满足k1>ϖ2,这样使得矩阵为正定矩阵,这样证明在控制律式(23)的作用下,控制系统是渐进稳定的.状态变量x1和x2会渐进收敛到零,即此外,可以由式(25)得出结论,V2从有界初始值V2(0)减少到零.因此,在式(23)的作用下,闭环系统中的所有状态变量都是有界的.证毕.

注1针对姿态运动学中的失配干扰Ξ1,在虚拟控制中设计了非线性干扰观测器式(16)来补偿失配干扰的影响.为了补偿未知的集总匹配扰动Ξ3,在控制指令中设计了非线性干扰观测器式(20).所提出的非线性干扰观测器在控制设计上简单有效,而观测器的性能只需调整一个参数就能实现.

注2在航天器姿态机动过程中,由于在轨航天器总是受到各种有效载荷和外部干扰等环境的影响,很难获取关于贮箱内液体燃料晃动的动力学特性.因此状态反馈控制律式(23)在实际应运中受到限制,在这种情况下,输出反馈控制策略能够很好的解决这种问题.

注3与上述控制器有关的一个问题是,控制器式(23)没有考虑控制输入饱和的情况,针对这种情况,引入指令滤波器补偿控制输入饱和.

3.2 输出反馈反步控制律设计

针对在实际应用中液体晃动位移变量难以测量的问题,将之前设计的状态反馈控制器延伸到输出反馈控制器,并且设计合适的自适应更新率对液体晃动位移变量进行估计,这样就得到了输出反馈控制器如下.

定理2针对机动控制系统式(12),设计如下控制律式(26a),并且自适应控制律式(26b),能够保证闭环系统的渐进稳定:

式中:eη为η的估计误差,eψ为ψ的估计误差.将式(27)对时间求一阶导数,然后将控制律(26)代入可得

式中:Γ可由Lyapunov方程ΓA+ATΓ−2Q计算,其中Q ∈R4为任意正定对称矩阵.根据第3.1节已经证明为正定矩阵,这样可以得到在控制律式(26)的作用下,闭环系统是渐进稳定的.

证毕.

3.3 输入饱和的输出反馈控制律设计

将第3.2节设计的控制律结合指令滤波器来设计输入饱和的控制律,图2描述了指令滤波器的工作原理.图2表示的是信号的滤波,经过指令滤波器可以产生一个幅度、速率和带宽受限的信号nc及其导数状态空间表示:

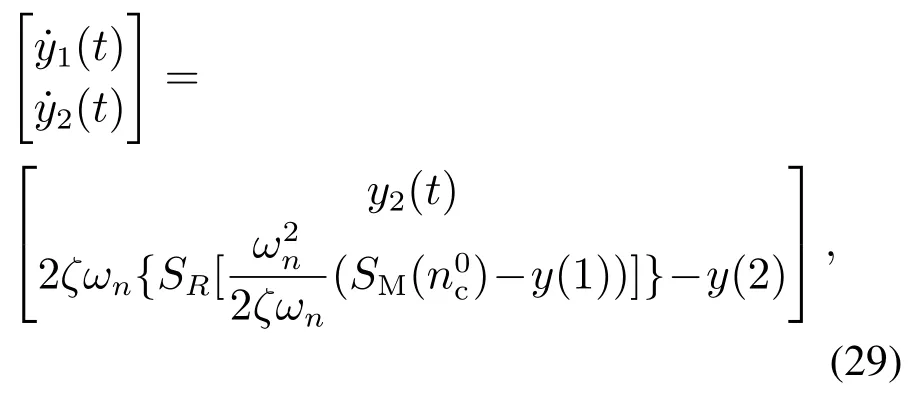
式中SM(x)和SR(x)分别代表幅度和速率限制函数,表示为

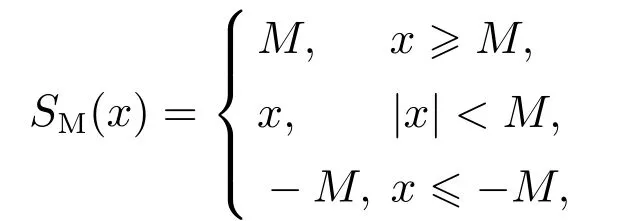
SR(x)与SM(x)定义相同.在函数SR(x)与SM(x)的线性范围内,滤波器的动态为

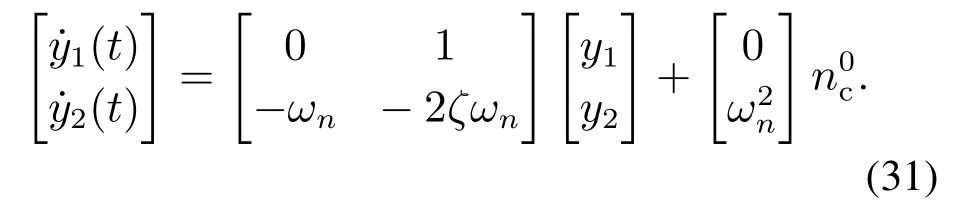
图2 指令滤波器结构图Fig.2 Structure of a command filter

注4这是一个典型的单位增益低通滤波器,指令滤波器可以过滤输入信号产生一个幅度、速率和带宽受限的信号nc及其导数.除此之外,另一个显著的优点是,计算导数时除了积分运算外没有任何微分运算.这些优点使得滤波器在设计输入饱和下的控制器将会是很好的工具.

利用上述指令滤波器的优点,输入饱和的控制器设计过程如下:

步骤1定义信号

式中ξ2将在随后的步骤4中定义.根据上述滤波器的工作原理,将会产生有界连续且幅值、速率和带宽受限的虚拟控制信号α及其导数˙α.接下来定义

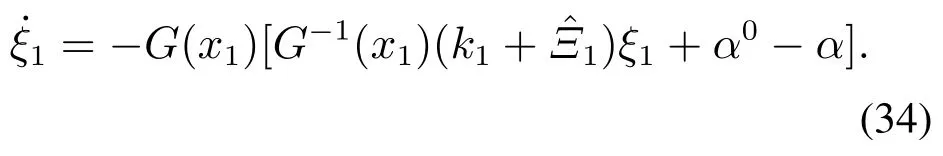
式(34)可以看作是ξ1的自适应算法,它的作用是将在随后的步骤2中对x1进行补偿.

步骤2定义补偿误差

步骤3定义未经过滤波器处理的控制输入

无论u0幅值多么大,当u0被过滤后,u0产生的u可以直接作为控制信号,而且u在幅度、速率和带宽这些方面都会得到限制.

步骤4定义ξ2的自适应算法,其目的是补偿步骤2中的x2:

假设4假设存在足够大的控制增益k1和k4满足如下不等式:

注5注意到上述假设4满足充液航天器姿态机动控制系统,原因在于:通过第3.1节的证明,可以得到系统状态变量x1,x2以及集总扰动估计误差都是有界变量,通过式(33)和式(34)可以得出补偿变量ξ1也是有界的.综上,存在足够大的控制增益k1和k4,使假设4成立.

至此,将本文最后的结论总结在如下的定理3中.

定理3对于充液航天器姿态机动控制系统式(12),设计式(33)−(38)的控制律,存在测量不确定以及控制输入饱和的情况下,能够保证闭环系统渐进稳定性.

证 考虑Lyapunov函数

将式(39)对时间求一阶导数可得

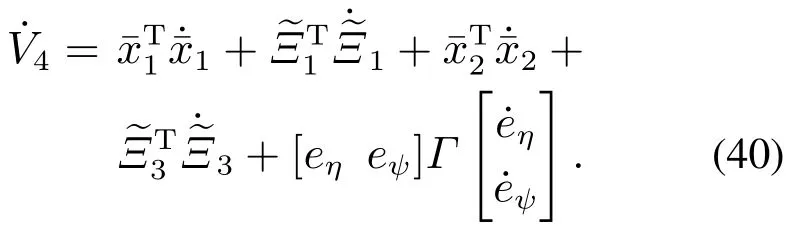
通过式(34)和式(35)可以得到

通过式(36)和式(38)可以得到

将式(37a)代入上式,进一步整理可得

将式(41)−(42)代入式(40)可得

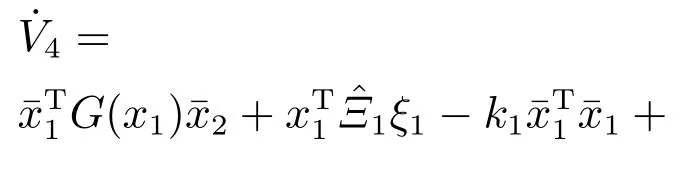
将式(37b)代入到上式,进一步整理可得

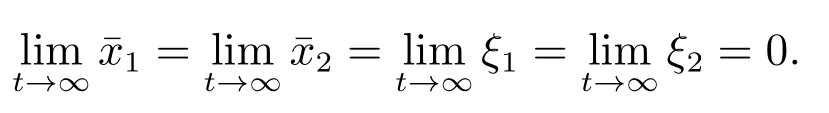
另外,需要注意的是,虚拟控制α和实际控制输入u在过滤后都会受到大小、速率和带宽的限制.此外,对SR(·)与SM(·)函数的幅值没有特定的限制,也就是说,对输入信号的约束可以随着实际不同执行器任意小.

证毕.

注6虽然SR(·)与SM(·)函数的幅值理论上可以设计得任意小,但如果选择得任意小,根据式(34)和式(38),补偿变量ξ1和ξ2会相当大,这将导致ξ1和ξ2的收敛时间较长.

4 数值模拟

选取刚体航天器转动惯量[8]

在仿真中,假设航天器受到的外部干扰为

控制器参数选择k130,k25,k35,k410,QI4.指令滤波器相关参数选取为[22]ωn2 rad/s,幅值限制选取10 N,速率限制选取为0.5 N/s.液体燃料相关参数选取为mb100 kg,mp0.1mb,l0.228 m,rx1.2 m,c1c20.05.假设航天器位于地球轨道高度800 km处[29],g等于当地的重力加速度,选取g7.689 m/s2.航天器角速度初始值ω(0)[0 0 0]T,液体晃动位移初始位移η(0)[0 0]T,初始姿态四元数误差q(0)[0.1763 −0.5264 0.2632 0.7896]T.此外,执行机构提供的最大输出幅值um10 Nm.仿真结果如图3−21所示.

图3 集总匹配干扰Fig.3 Lumped matched disturbances

图4 集总失配干扰Fig.4 Lumped mismatched disturbances

情形1只考虑输出反馈反步控制律.仿真结果如图5−10所示.

图5 测量的姿态角速度响应Fig.5 Measured angular velocities response vs.time

图6 测量的姿态四元数响应Fig.6 Measured attitude quaternions response vs.time

图7 液体晃动位移变量及其估计值响应Fig.7 Liquid sloshing displacement and its estimated displacement response vs.time

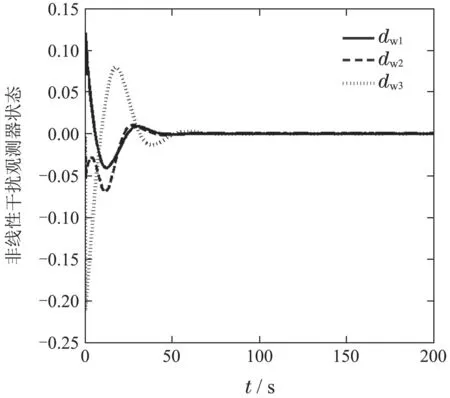
图8 非线性干扰观测器状态响应1Fig.8 State response of a nonlinear disturbance observer one

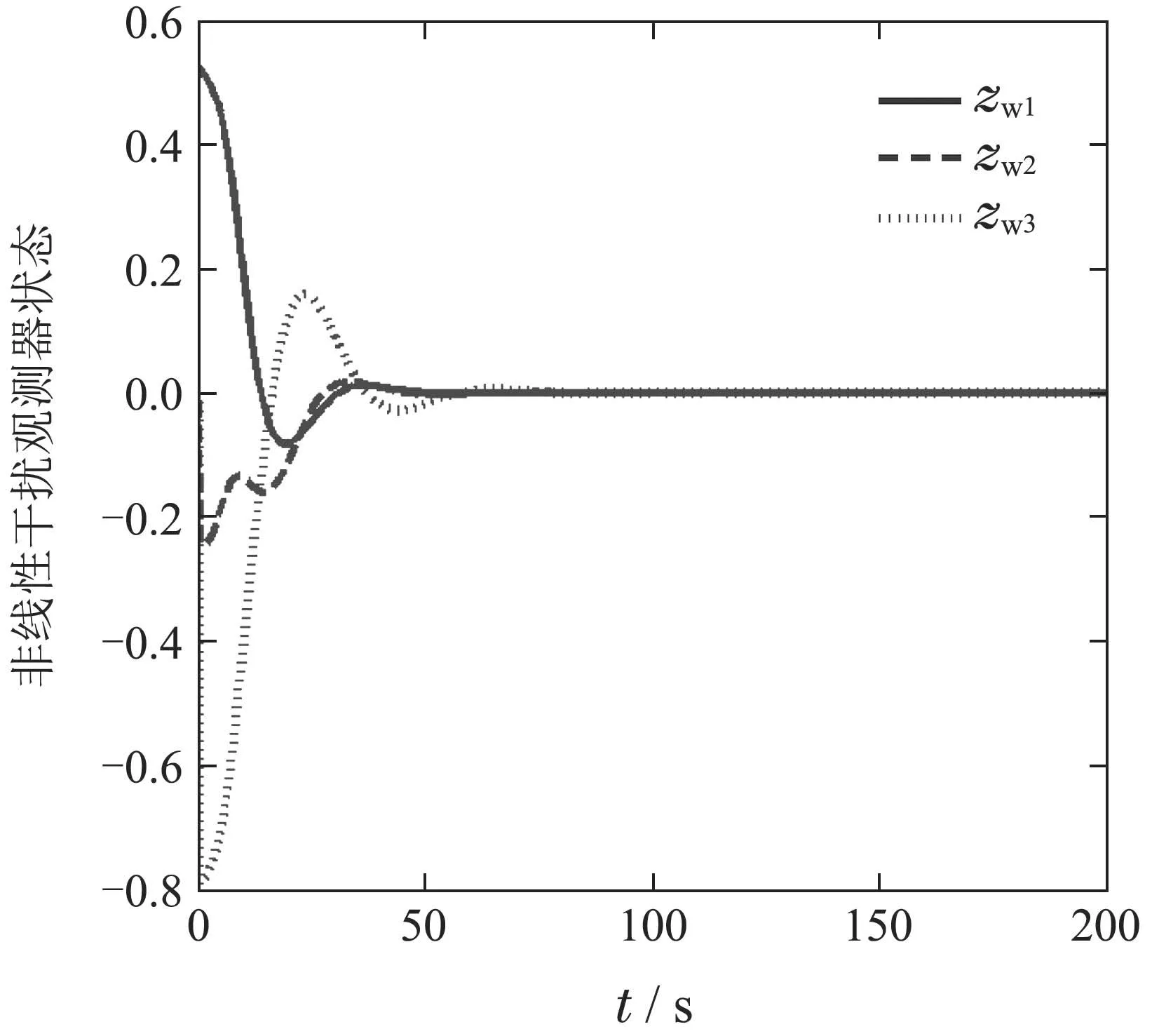
图9 非线性干扰观测器状态响应2Fig.9 State response of a nonlinear disturbance observer two

图10 控制力矩响应Fig.10 Control torque response vs.time

情形2考虑输出反馈反步控制律结合指令滤波器.仿真结果如图11−21所示.

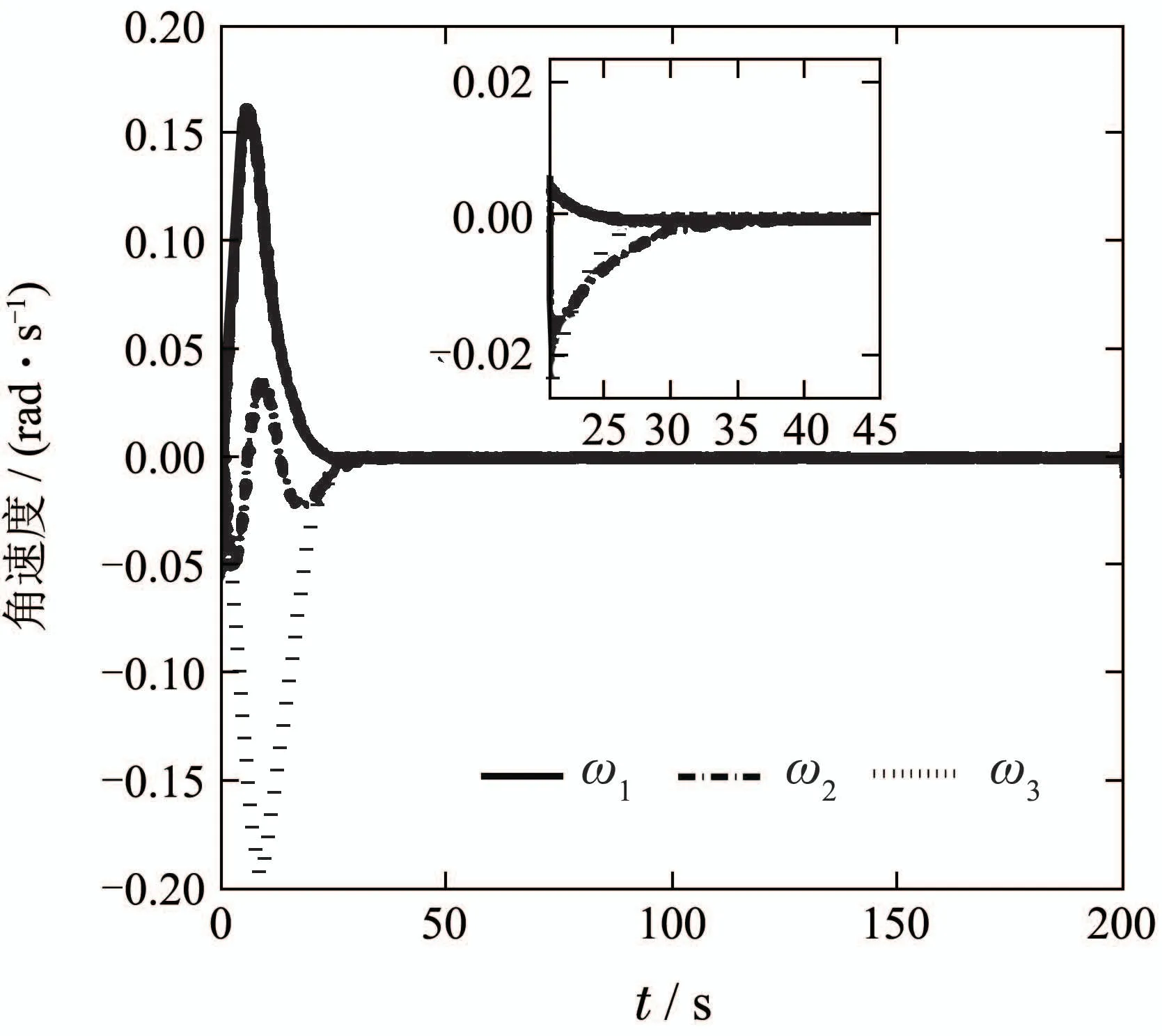
图11 测量的姿态角速度响应Fig.11 Measured angular velocities response vs.time

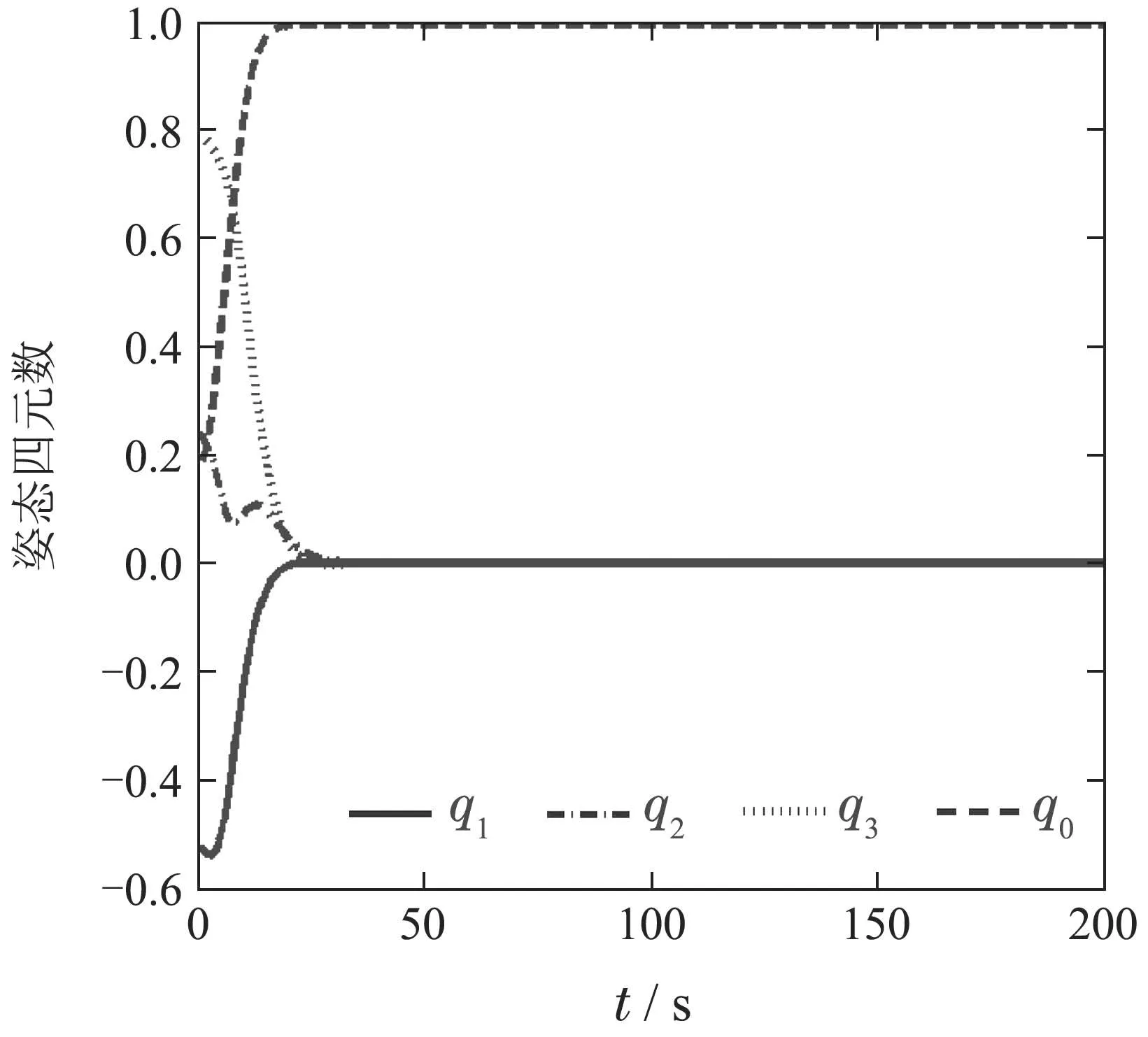
图14 实际的姿态四元数响应Fig.14 Actual attitude quaternions response vs.time

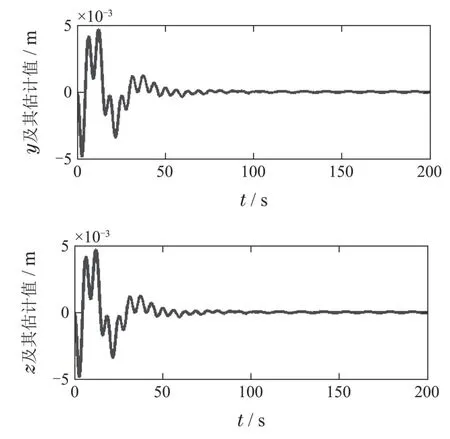
图15 液体晃动位移变量及其估计值响应Fig.15 Liquid sloshing displacement and its estimated displacement response vs.time

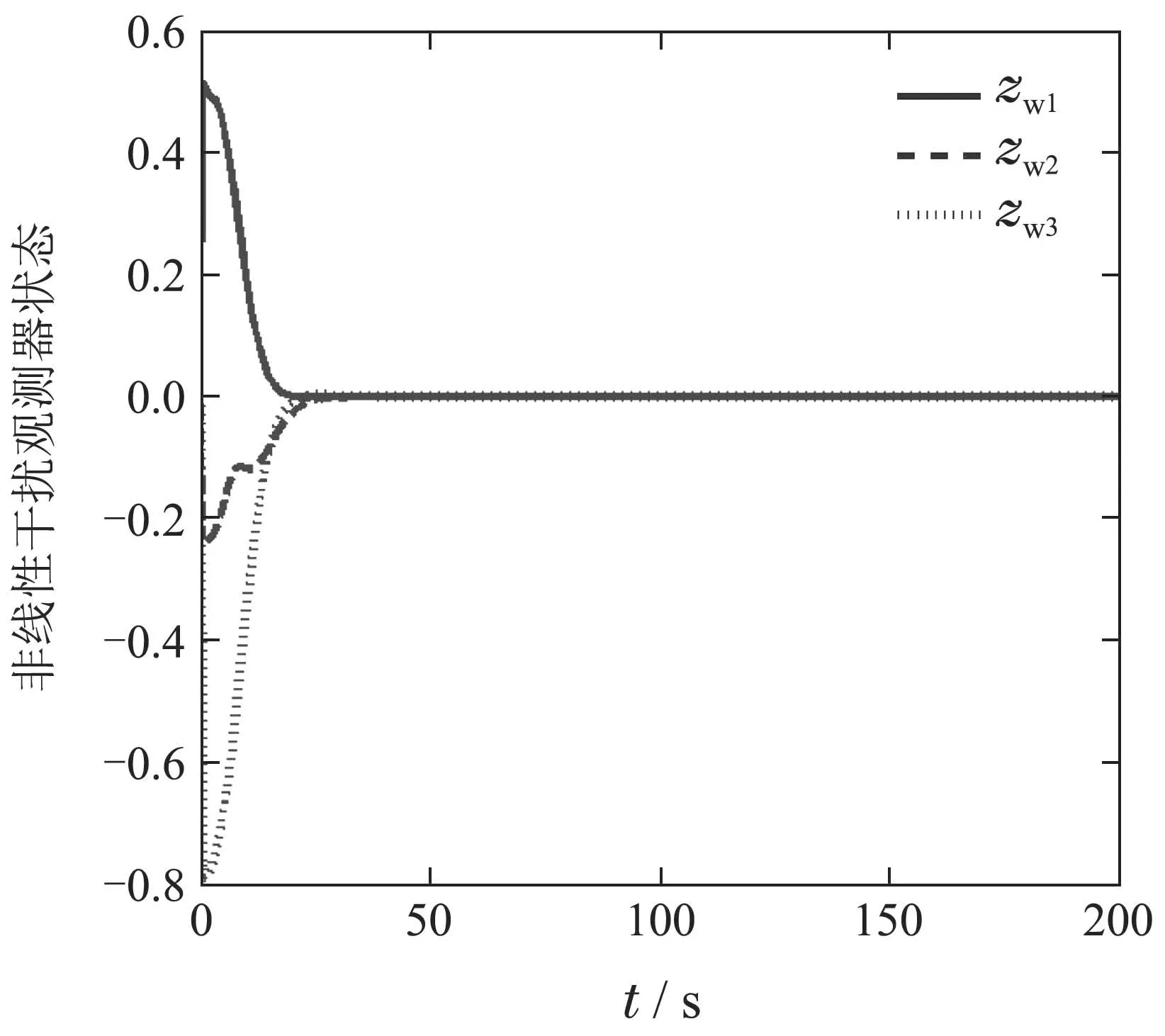
图16 非线性干扰观测器状态响应1Fig.16 State response of a nonlinear disturbance observer one vs.time

图17 非线性干扰观测器状态响应2Fig.17 State response of a nonlinear disturbance observer two vs.time

图18 指令滤波器状态响应1Fig.18 State response of command filter one vs.time

图19 指令滤波器状态响应2Fig.19 State response of command filter two vs.time

图20 控制力矩响应Fig.20 Control torque response vs.time

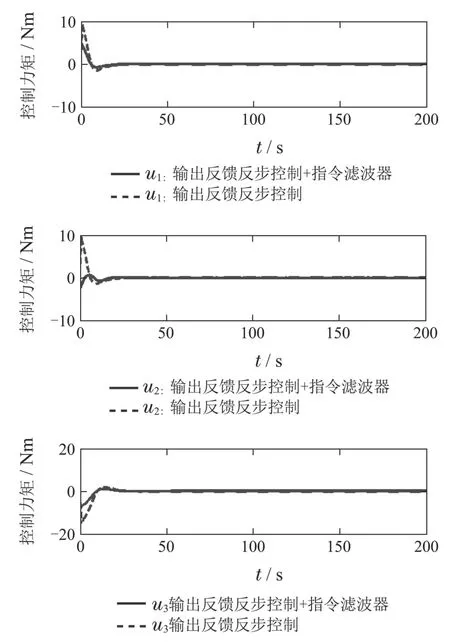
图21 两种情形的控制力矩对比Fig.21 comparison of control torque for two cases

仿真分析如下:

1)图3和图4分别给出仿真中两种集总扰动时间历程图.图5和图6分别为姿态角速度和姿态四元数的时间历程图,如图5−6所示,姿态和角速度在60 s内收敛到平衡位置,具有平滑的瞬态响应性能.这意味着所提出的输出反馈反步控制器很好地抑制了模型不确定性和测量不确定性.

2)图7为液体晃动位移变量时间历程图,由图可以看出,液体晃动位移变量幅值≪0.01 m,表明提出的输出反馈反步控制器能够有效克服液体晃动对航天器姿态机动稳定性的影响.在晃动位移变量未知的情况下,所设计的自适应更新率能够有效估计位移变量.

3)图8和图9给出非线性干扰观测器的状态,由图可以看出,干扰器状态渐进的收敛的平衡位置,这表明通过选择合适的观测器增益可以有效补偿参数不确定,外部干扰,测量不确定引起的不利影响.图10给出控制力矩时间历程图,可以看出,控制力矩光滑平稳且力矩幅值限定在|u(t)|15 Nm.

4)图11和图12为考虑输入饱和的条件下,测量的角速度和姿态四元数的时间历程图.相比较图5和图6而言,由图11和图12可看出:姿态角速度和姿态四元数响应时间缩短,大约30 s左右时间收敛到平衡位置,而且具有良好的平滑的瞬态响应性能.这表明加入指令滤波器可以很好的改善控制系统的响应.图13和图14为实际的角速度和姿态四元数,可以看出实际的角速度和姿态四元数也渐进收敛到平衡位置.

5)图15为液体晃动位移变量时间历程图,晃动位移变量幅值<0.005 m,相比较图7可以看出,图15的晃动位移变量远远小于图7的位移变量,这表明加入滤波指令可以实现对液体晃动的有效抑制,进而克服液体晃动对航天器姿态机动的影响.

6)图16和17为非线性干扰观测器的状态时间历程图,相比较图8和图9,图16和图17收敛速度快,表明加入指令滤波器能够缩短干扰补偿器对集总扰动的补偿时间.图18和图19为指令滤波器的状态时间历程图.由图可以看出,滤波器状态也能渐进收敛到平衡位置,表明滤波器可以有效补偿反步变量x1和x2,进而有效补偿控制输入饱和对控制系统的不利影响.

7)图21为输出反馈反步控制结合指令滤波器的控制力矩时间历程图,由图可以看出,控制力幅值|u(t)|8 Nm,相比较图10而言,加入指令滤波器后,力矩幅值大幅度降低,若引入能量指标很容易看出图20完成大角度姿态机动需要较少的能量,而且控制力矩响应保留了图10光滑平稳的特性.

综上所述,考虑在轨航天器控制系统中存在外部未知干扰,参数不确定,测量不确定,控制输入饱和的条件下,本文提出的饱和输出反馈复合控制律可以实现航天器姿态机动的稳定性.仿真结果验证了控制方法的有效性.

5 结论

本文以三轴稳定充液航天器为研究对象.首先将晃动液体燃料等效为球摆模型,利用动量矩守恒定律推导出航天器固液耦合动力学模型.考虑在轨机动的航天器存在外部未知干扰,参数不确定,测量不确定以及控制输入饱和的问题,同时,考虑贮箱内晃动液体位移变量不可测量的特性,基于经典反步法结合非线性干扰观测器和指令滤波器提出了一种饱和输出反馈反步控制策略.将外部未知干扰,参数不确定和测量不确定看作集总扰动,非线性干扰观测器对这种集总扰动可以实现有效补偿,指令滤波器可以实现对控制输入饱和的补偿.所提出的控制策略,即保留了反步控制法的优点,又能利用非线性干扰观测器和指令滤波器的补偿能力消除对模型不确定和控制输入饱和的不利影响.Lyapunov稳定性分析方法证明了闭环系统的渐进稳定性.仿真结果表明本文提出的控制方法的有效性.