一类时变时滞车辆跟驰模型的稳定性控制

杜文举 ,李引珍 ,张建刚 ,俞建宁

(1.兰州交通大学交通运输学院,甘肃兰州 730070; 2.兰州交通大学数理学院,甘肃兰州 730070)

1 引言

随着社会经济的迅猛发展和城市规模的不断扩大,交通拥堵问题已然成为世界范围内急需解决的共同难题.交通流的稳定性是研究交通道路中的扰动对交通流状态的影响.如果系统处在不稳定时,小扰动会沿着交通流向后传播,使得畅行的车流出现交通阻塞.如果系统处在稳定状态时,在传播的过程中小扰动会逐渐减小甚至会消失或者最终保持在一定范围内,使交通车流能顺利通行.交通流模型主要分为宏观模型、微观模型和介观模型,其中微观交通流模型主要包括元胞自动机模型和跟驰模型.车辆跟驰模型将交通流中的车辆看成分散的质点,在没有超车的情况下,通过观察单个车辆跟驰前车的方式来了解单车道交通流的特性.近年来,不少学者已经对车辆跟驰模型进行了研究[1–6].Zhang等[7]研究了经典车辆跟驰模型的稳定性,并通过线性化和数值积分分析了非线性模型.Orosz等[8]针对环形单车道上n辆车的最优速度跟踪模型,研究了不同波数下均匀流平衡的稳定性和分岔周期解.Zheng等[9]提出了一类扩展的车辆跟驰模型,考虑了同时包含车辆与前面车辆之间的速度差的控制信号,并应用控制理论方法研究了模型的稳定性.杨龙海等[10]采用高精度车载GPS设备获取基于时间序列的车辆跟驰数据,根据实测车头间距–平均速度关系构建了改进的优化速度函数,对原优化速度函数和改进的优化速度函数进行了参数标定,并对两个函数进行了微观向宏观交通参数的推导.Zhai等[11]在考虑谨慎型和激进型驾驶行为的基础上,提出了一类新的最优速度跟驰模型,并给出了该模型的线性稳定性条件.秦严严等[12]基于智能网联车辆跟驰特性,考虑多前车电子节气门角度反馈,构建智能网联车辆(connected autonomous vehicle,CAV)跟驰模型,并应用稳定性分析方法得到模型稳定性判别条件.目前,对跟驰模型的稳定性的研究采用线性化处理会导致不准确的结果,特别是在临界条件附近,系统小扰动信息可能会产生意想不到的演化结果.而非线性稳定性分析方法,仍然是忽略掉方程高阶项得到的,还是不可避免地存在误差.此外,传统的跟驰模型的稳定性分析方面的研究基本上都是假设车道上所有车辆具有相同的初始速度和初始车头间距,即车辆跟驰系统的稳定状态,然后讨论跟驰车队中头车或者中间的某辆车改变运行状态对整个跟驰系统稳定性的影响,没有考虑受到随机外部干扰之后如何通过控制策略使其趋于稳定.

此外,在实际系统中经常存在着噪声或扰动,它们经常会引起系统的不稳定.因为有外部扰动的存在,在复杂网络的实际应用中,必须考虑不确定性因素.为了避免或者消除这种随机外部扰动的影响,我们需要对具有外部扰动的复杂网络的同步控制进行研究.因为随机外部扰动广泛的研究背景,其在复杂网络中的研究得到了许多学者的关注,而它与网络同步之间的关系也成为了研究的热点.Li等[13]研究了受外界干扰的线性复杂动态网络的扰动抑制问题.Zheng等[14]应用基于观测器的控制研究了一类复杂动态网络的鲁棒H∞同步问题.Li[15]提出了一种新的H∞聚类同步概念以量化复杂网络的外部干扰,并以线性矩阵不等式的形式导出了H∞聚类同步判据.郭凌等[16]对一类带有外部扰动和时变时滞的Lurie系统的聚类同步进行了研究.Shen等[17]研究了具有时变时滞和半马尔可夫跳变拓扑的复杂网络的有限时间H∞同步问题.Liu等[18]采用滑模控制方法研究了相位式半马尔可夫开关主从式系统的H∞同步问题.Ho等[19]通过泊松过程讨论了非线性随机耦合网络的鲁棒同步问题.Wang等[20]利用Lyapunov泛函和Barbalat引理分析了多重权复杂网络的输出同步问题,同时还讨论了多重权复杂网络的H∞输出同步问题.本文主要基于复杂网络的同步理论,通过设计基于速度和车头间距的自适应控制器对一类考虑前后车效应的时变时滞最优速度车辆跟驰模型的稳定性进行了研究.

2 时变时滞车辆跟驰模型

1995年,Bando等[21]基于“速度–车间距函数”的概念,提出了如下最优速度模型:

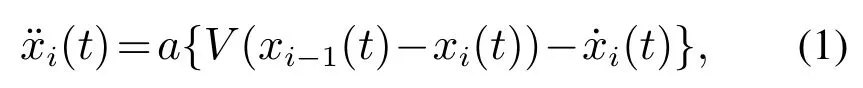
式中: a 是加速度常数,也称为司机的敏感性系数;V(h)为“速度–车间距函数”.该模型能很好的描述交通流的数学与物理性质,所以在交通流领域,受到了学者的广泛关注与研究.

2014 年,李树凯等[22]基于Lyapunov 稳定性理论,通过反馈控制策略,研究了如下考虑驾驶员反应存在滞后时间的非线性车辆跟驰模型的稳定性问题:

然而,该模型认为驾驶员在调整车速时仅依靠本车与前车之间的车间距来调整车辆的速度,但经过实际的分析发现驾驶员在调控的过程中有时还会受到后车的影响.针对同时考虑前后车的影响,葛红霞等[23]考虑前后临近车辆对当前车速度的影响,提出一个同时考虑前后车影响的车辆跟驰模型.然而,该模型中没有考虑驾驶员接受信息和采取应对措施之间存在滞后时间.Zhai等[24]同时考虑了前后车的影响和驾驶员接受信息和采取应对措施之间存在的时变滞后时间,提出了一类新的跟驰模型并利用控制理论研究了模型的稳定性问题.基于控制理论的车辆跟驰模型稳定性的控制分析,基本上都是通过添加一些控制项来提高交通流的稳定性,没有考虑平稳的交通流受到随机外部干扰之后如何通过控制策略使其趋于稳定.因此,本文同时考虑前后车效应以及驾驶员的反应时间存在时变滞后时间,提出考虑前后车效应的时变时滞最优速度车辆跟驰模型,并基于复杂网络同步理论,设计同时基于速度和车头间距的自适应控制器,更加精确快速的控制车辆跟驰模型的稳定性.

基于此,本文同时考虑前后车效应以及驾驶员的反应时间存在滞后时间,研究如下考虑前后车效应的时变时滞最优速度车辆跟驰模型:

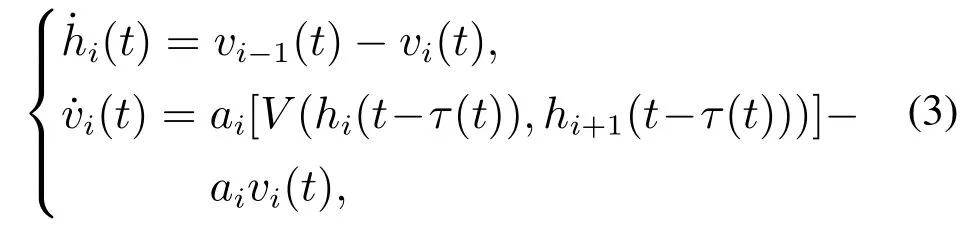
式中: ai表示第i辆车的司机在行驶过程中的敏感系数,vi(t)表示t时刻第i辆车的速度,vi−1(t)表示t时刻第i −1辆车的速度,hi(t)表示t时刻车道中第i辆车与前方车辆i −1的车头间距,hi+1(t)表示t时刻车道中第i辆车与后方车辆i+1的车头间距.

葛红霞等[23]在其模型中的优化速度函数既依赖于与前车之间的车头间距,也依赖于与后车之间的车头间距,具体形式如下:

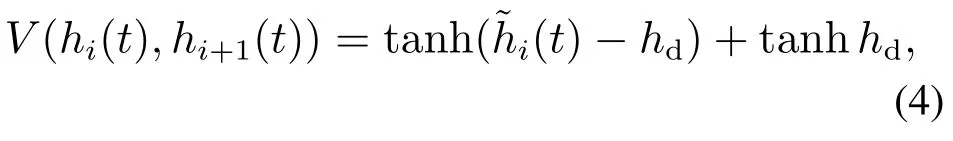
其中τ1,τ2都是恒定常数,且τ1表示由驾驶员理性行为产生的最大反应时间延迟,τ2表示关于车头间距滞后时间的变化率.此外,对于方程(3),初始的hi(t)为:hi(t)ϕi(t), t∈[−τ1,0], i1,2,···,N,其中ϕi(t)为连续可微函数.

本文假定当前车辆同时受到前后车辆的影响,且车头间距存在着随时间变化的滞后时间,与以往研究相比更贴近现实,更能反映真实的交通行为.

引理1[22]V(hi(t))是一个连续的、非负的单调递减函数,并且存在常数k >0,使得对∀hi(t),hj(t)∈Rn,都有

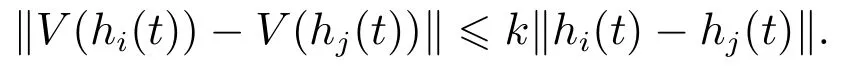
3 外部扰动下时变时滞复杂网络的同步理论

考虑由N个具有时变时滞的节点组成的含有外部扰动项的复杂动态网络,其模型如下:

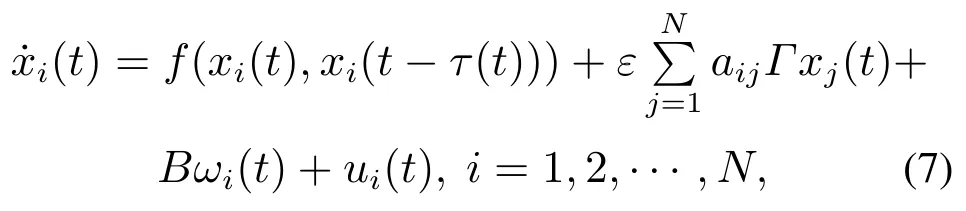
式中:xi(t)(xi1(t)xi2(t)··· xin(t))T∈Rn表示第i个节点的状态变量;f(·):Rn×R →Rn是一个光滑的非线性连续向量值函数;Γ(γij)n×n∈Rn×n是已知的内部耦合矩阵;ε为网络(7)的内部耦合强度;τ(t)是节点的时变时滞,它连续可微且满足τ <∞,其中τ是已知的非零常数;矩阵A(aij)∈RN×N表示网络(7)的拓扑结构,满足耗散耦合条件aii其中aij的具体定义如下:若节点i 和节点j 之间有连边,则aij>0,否则aij0(ij,i,j1,2,···,N);ωi(t)为外部干扰,B为一个常数矩阵,决定了外部干扰ωi(t)的强度;ui(t)是所需设计的控制器.

令同步误差ei(t)xi(t)−s(t),i1,2,···,N,则误差系统定义为

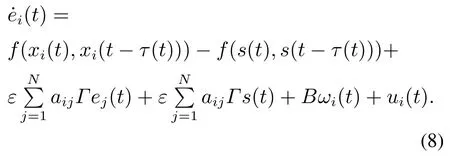
定义1对于给定的扰动衰减系数γ >0,以及对称正定矩阵S,如果下面的条件成立:

a)当ωi(t)0时,在控制器ui(t)作用下,同步误差系统(8)渐近自适应稳定;

b)当ωi(t)0时,在初始条件为零的条件下,若同步误差系统(8)满足

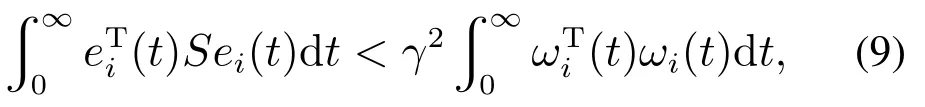
则称网络(7)实现了自适应H∞同步.

引理2[25]对任意给定的矩阵X,Y ∈Rn×m,都有下列矩阵不等式成立:

其中A ∈Rn×n且ATA>0.

假设1τ(t)是可微函数且(常数延迟是该假设的特例).

假设2对所有xi(t),yi(t)∈Rn,存在矩阵K1,K2∈Rn×n使得

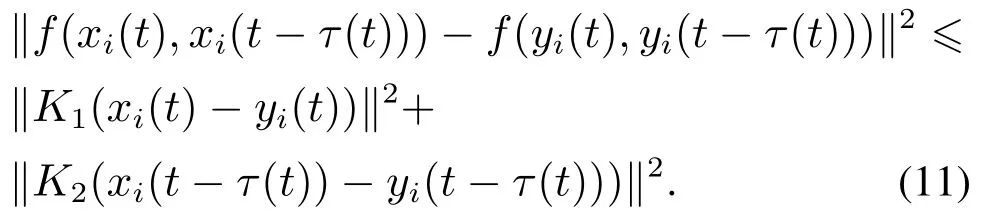
假设3对∀x(t),y(t)∈Rn和t>0,存在一个正定的对角矩阵P和数γ >0,η >0,使得

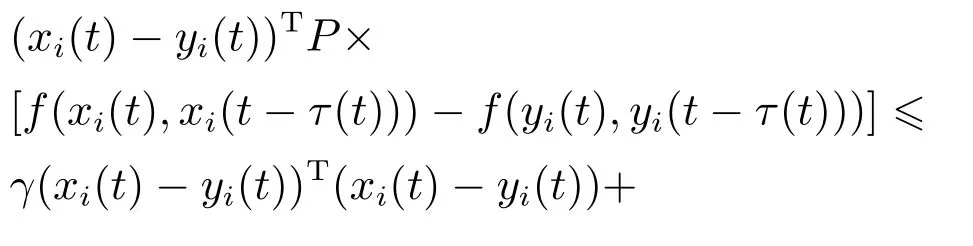
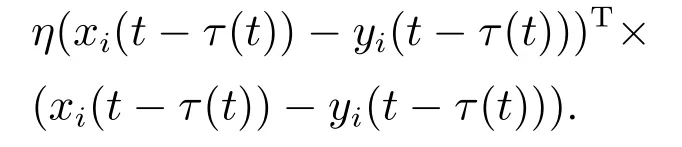
定理1当外部扰动ωi(t)0时,对于给定的对称正定矩阵S和γ >0,如果假设1–2成立,且存在正定矩阵P和Q以及足够大的˜d,使得

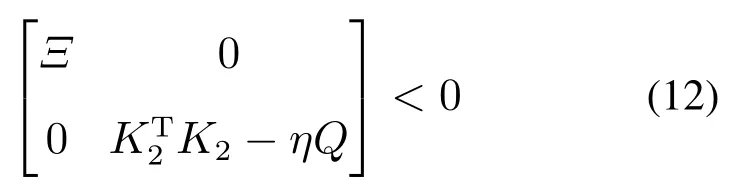
成立.那么,在控制器

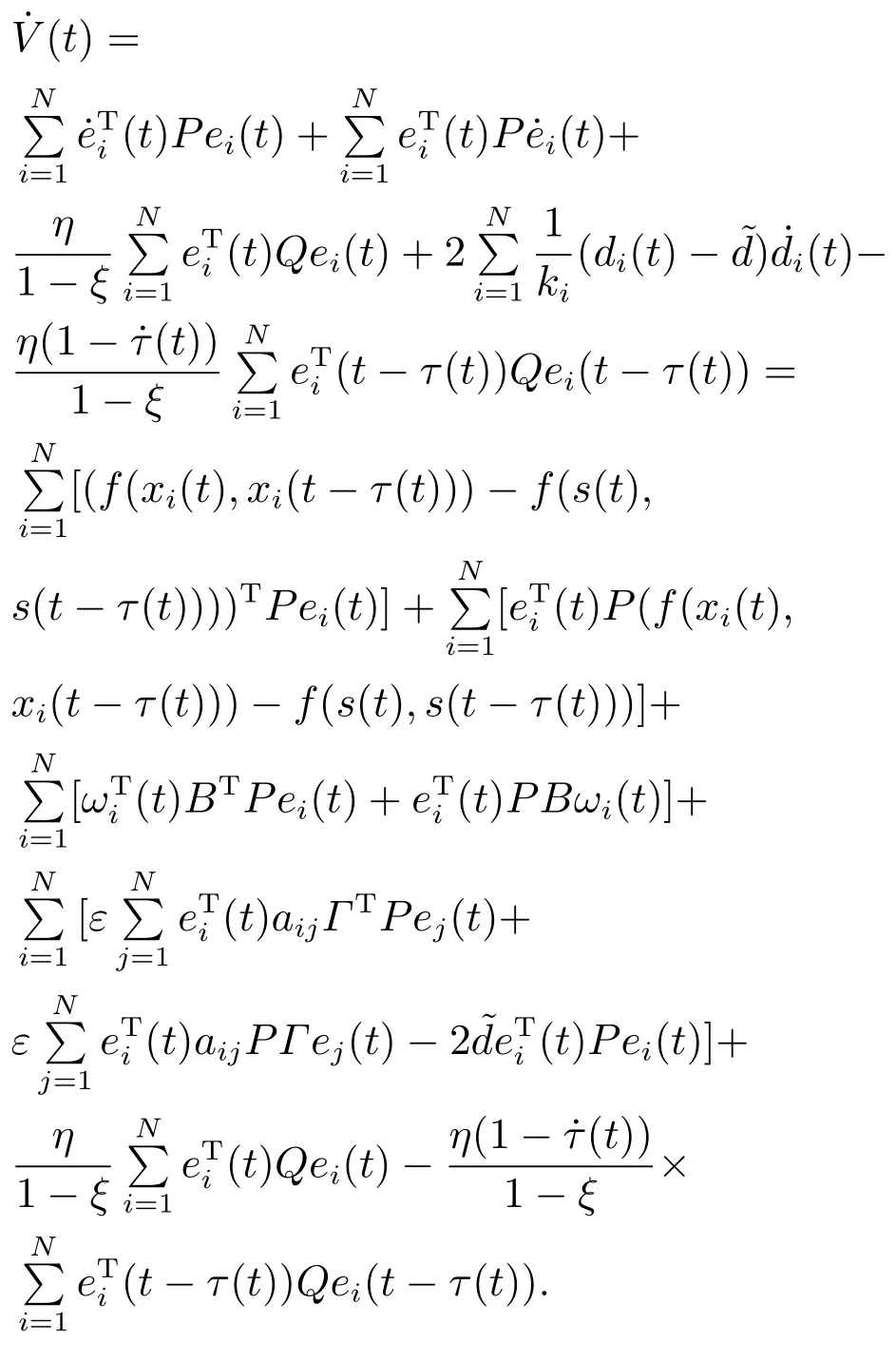
根据假设1–2以及引理2,可得

从而网络(7)在扰动衰减水平为γ的情况下达到了自适应H∞同步.证毕.

推论1当外部扰动ωi(t)0时,如果假设1,3成立,且存在正定矩阵P 和足够大的使得(γ+I +εa′PΓ −<0,那么,网络(7)在控制器(13)的作用下实现自适应同步.

4 基于复杂网络同步的车辆跟驰模型稳定性控制

利用复杂网络的同步控制理论研究车辆跟驰模型的稳定性,是将行驶在车道上的每一辆车视为复杂网络的一个节点,车辆之间如果存在通讯关系则构成复杂网络的虚拟边,即车辆间通信关系就可以构成复杂网络的邻接矩阵.以车辆为节点、车辆间通讯关系为边构成的复杂网络同步,即车道上跟驰车队中所有车辆都以相同的理想速度,并保持相同的理想车头间距有序的行驶.对于行驶在单车道上的N辆车,每一辆车视为网络的一个节点,令矩阵A(aij)∈RN×N表示车辆间通信关系的邻接矩阵,其中aii且aij定义如下:如果车辆j是车辆i(j)的前方最近邻车辆,则aijaji1;否则aij0.对于任意一辆车i(i2,3,···,N)都受到前方最近邻车辆i −1的影响,同时也会受到后方最近邻车辆i+1的催促作用.因此,可以得到如下车辆运动的邻接矩阵:

若车辆的理想速度为v0(t),理想的车头间距h0(t),本文的目的是要利用复杂网络同步理论,通过设计基于速度和车头间距的自适应控制器,使得所有车辆都以速度v0(t),并保持车头间距h0(t)有序的行驶.

4.1 时变时滞车辆跟驰模型的稳定性控制

当外部扰动ωi(t)0时,考虑单行道上行驶的N辆车,以模型(3)为网络的节点,则网络的节点动力学方程为

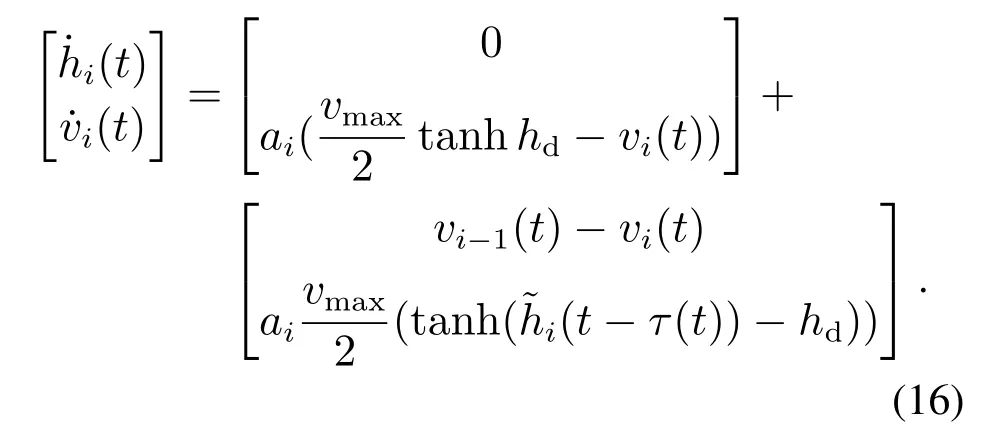
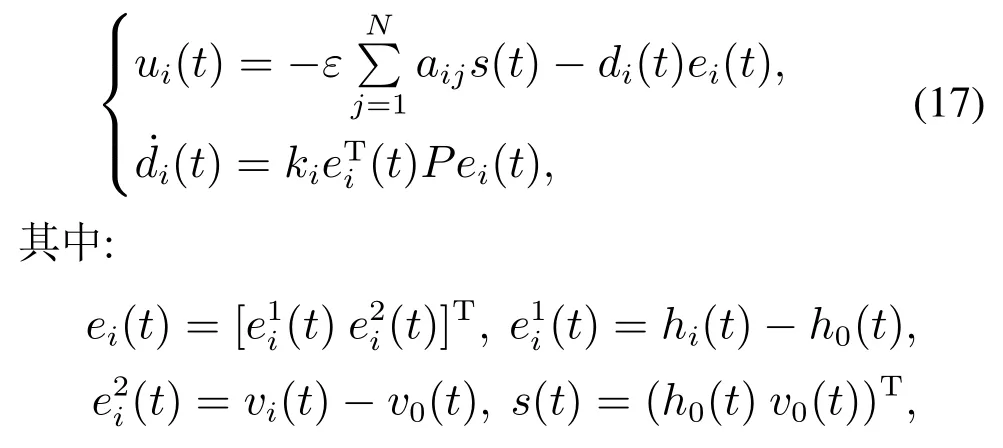
因为ωi(t)0,则由式(7),对网络中的第i(1iN)个节点有

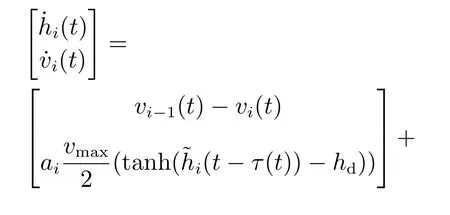
为了满足假设3,选取适当的参数δ >0,使得

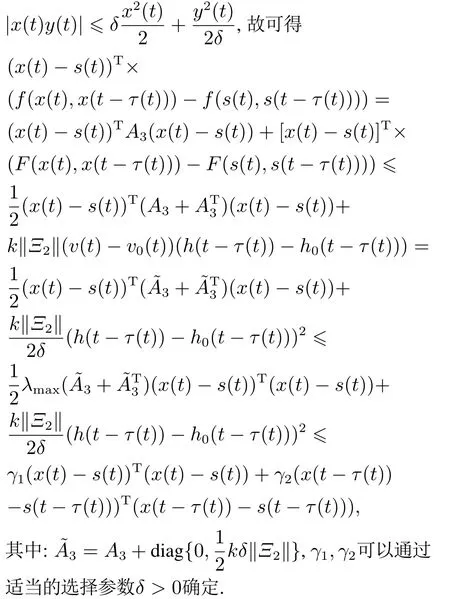
因此,由上式可知假设3成立,且由式(6)知假设1成立.根据推论1,若存在正定矩阵P和足够大的使得那么,跟驰模型在控制器(17)的作用下趋于稳定,即所有的车辆都以速度v0(t),并保持车头间距h0(t)有序的行驶.

4.2 外部扰动下时变时滞车辆跟驰模型的稳定性控制

当外部扰动ωi(t)0时,同样考虑行驶在单行道上的N辆车,以模型(3)为网络的节点,则由式(7),网络的第i(1iN)个节点的动力学方程为

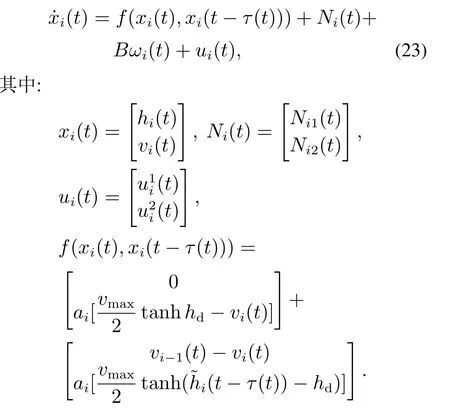
下面将式(23)化成以下形式:

由上式可知,假设2成立,且由式(6)知假设1成立.从而根据定理1,如果存在正定矩阵P和足够大的使得式(12)成立,那么网络在控制器(13)的作用下就可以达到自适应H∞同步,即在受到随机外部扰动的情形下,加入控制器后所有的车辆都以速度v0(t),并保持车头间距h0(t)有序的行驶.

5 数值仿真

在接近开放边界条件下对模型进行仿真,考虑行驶在单车道上的20 辆车.模型中参数的取值为ε0.6,hd2 m,理想速度为v0(t)5.56 m/s,理想的车头间距h0(t)7.02 m.同时假设所有驾驶员的敏感系数都相同,即ai1.2 s−1,i1,2,···,20.考虑前方车辆及其后方车辆对当前车速度的影响,在驾驶员实际行驶过程中,对前车的敏感系数会大于对后面车辆的敏感程度,所以令α10.8, α20.2.驾驶员感应车头间距的滞后函数为τ(t)0.5+0.1 cos t,这里τ10.6,τ20.1.此外,假设所有车辆具有相同的参数,初始的车头间距hi(0)在区间[6.5,12]内随机选取,初始速度vi(0)在区间[3.5,8]内随机选取,车辆的初始速度和初始的车头间距都不相等,研究结果更具有一般性.首先,对模型不加控制器,得到车头间距hi(t)与速度vi(t)随时间的演化曲线,如图1所示.由图1看到,在没有加入控制器的情况下,整个跟驰系统都没有趋于稳定,也就是说出现了交通拥堵现象.

图1 未加控制器时车辆的车头间距和速度随时间的演化曲线Fig.1 The evolution curves of lateral distance,headway distance and velocity without controller

下面,将控制器加入到模型中,取参数ki0.5,i1,2,···,20,其他参数保持不变,可以得到如图2所示的误差收敛曲线以及hi(t)与vi(t)随时间的演化曲线.由图2(a)(c)看到,所有的车头间距hi(t)(i1,2,···,19)与本文设置的理想的车头间距h0(t)的差值在92个时间单位都趋于0;同时所有的车辆的车头间距hi(t)在92个时间单位趋于h0(t)7.02 m.由图2(b)(d)看到,所有的车辆的速度vi(t)(i1,2,···,20)与头车的速度v0(t)的差值在92个时间单位都趋于0;同时所有车辆的速度vi(t)在92个时间单位趋于v0(t)5.56 m/s.这表明,加入了控制器后,系统在92个时间单位就达到稳定状态,即加入控制器后,使得车辆行驶顺畅,明显地缓解了交通拥堵.

此外,保持其他参数不变,令参数ai0.5 s−1,i1,2,···,20,观察司机的敏感性系数对交通流稳定性的影响.由图3看到,交通流大约在106个时间单位才达到稳定.与图2相比,交通流达到稳定的时间延迟了14个时间单位.这说明,司机的敏感性系数对交通流的稳定性有一定的影响.因此,有关部门应该加强监管和宣传力度,尽量不要让司机疲劳驾驶、带病驾驶、避免让高龄司机驾驶等,有利于缓解交通拥堵、避免交通事故.

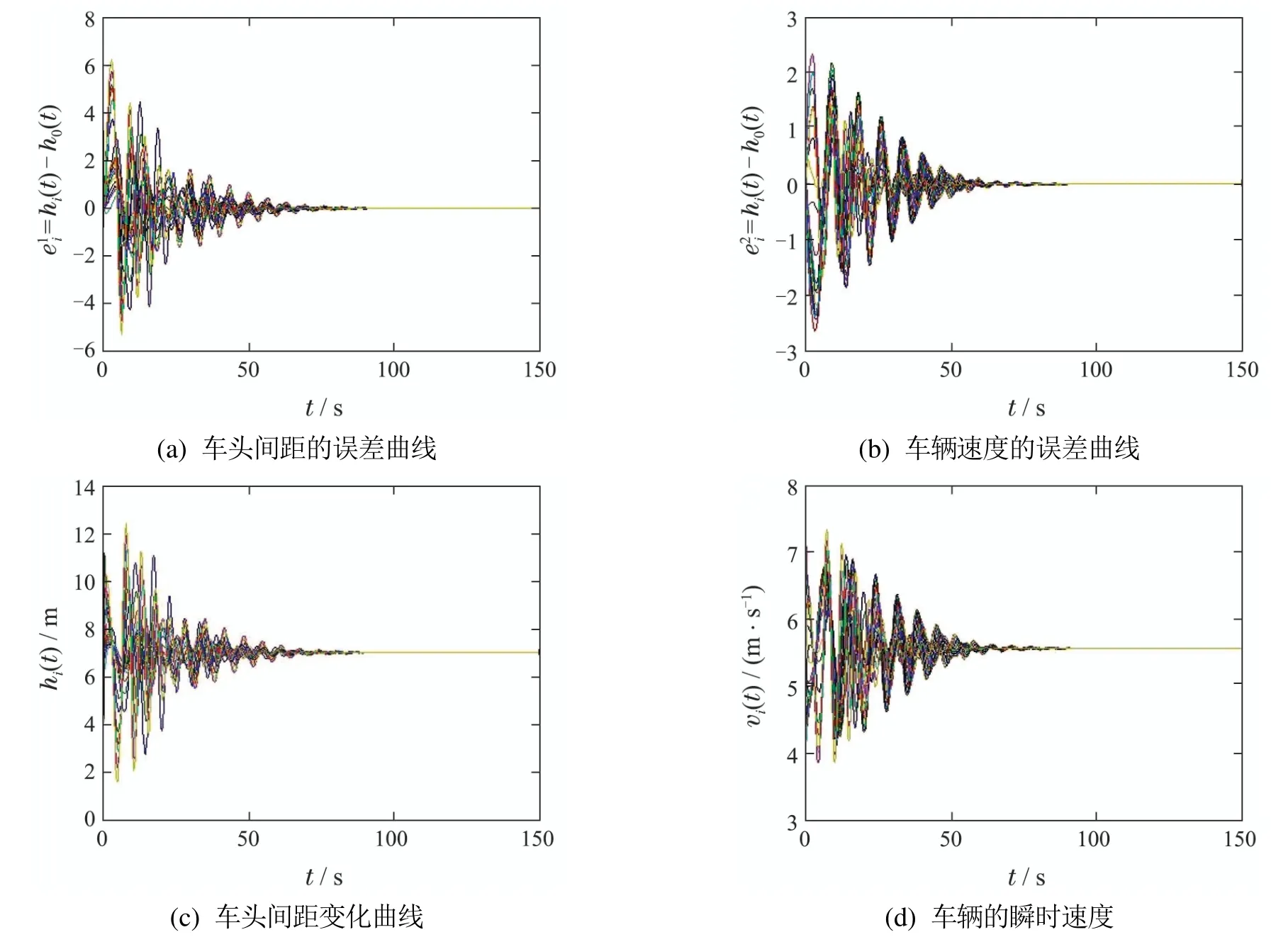
图2 加入控制器时车辆的车头间距和速度随时间的演化曲线Fig.2 The evolution curves of lateral distance,headway distance and velocity when adding the controller

图3 ai=0.5 s−1,i=1,2,···,20时车辆的车头间距和速度随时间的演化曲线Fig.3 The evolution curves of lateral distance,headway distance and velocity when ai=0.5 s−1,i=1,2,···,20

下面考虑在随机外部扰动的情形下,车辆跟驰系统的稳定性.假设对第3,8,13辆车施加如下的外部扰动:

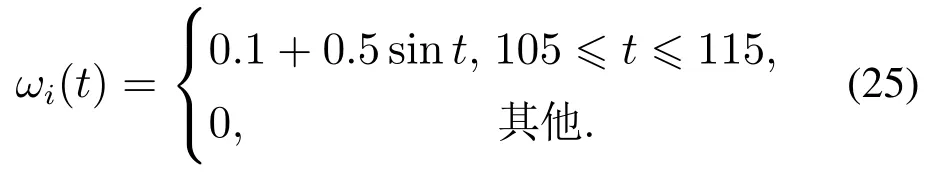
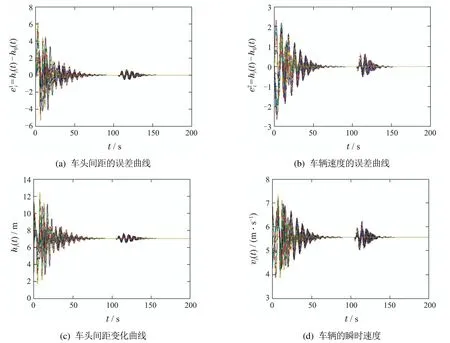
图4 外部扰动下车辆的车头间距和速度随时间的演化曲线Fig.4 The evolution curves of lateral distance,headway distance and velocity with external disturbance

6 结论

本文针对考虑前后车效应的时变时滞最优速度车辆跟驰模型,利用时变时滞复杂网络的自适应H∞同步理论,研究了该模型的稳定性问题.数值仿真结果表明:考虑前后车效应的时变时滞最优速度车辆跟驰模型在本文设计的控制器下快速趋于稳定,有效的缓解了交通拥堵.本文研究的主要内容是运用时变时滞复杂网络同步理论解决跟驰模型中的交通堵塞问题,得到的结论可以为预防和控制跟驰模型中的交通拥堵提供理论依据.