考虑恶化效应的MapReduce模型下的同类机调度
黄基诞
(东华大学旭日工商管理学院,上海 200051)
1 引言
许多经典的排序问题研究文献中都假定工件的加工时间是一个常数[1].而在现实生产制造业中,尤其在玻璃、医疗、塑料、钢铁等行业中,工件的加工时间经常根据不同的开工时间而改变.在调度问题中,部分工件的加工处理时间可能随着其开工时间的推后而延长,这类工件被称为恶化工件.PEI等[2]研究的恶化效应是指工件实际加工时间与资源数量有线性依赖关系的调度问题,在改进的蝙蝠算法中,利用变邻域搜索策略对算法进行改进并对问题进行求解.Ding等[3]研究了工件实际加工时间与加工顺序产生恶化效应的调度问题.此外,文献[4–7]研究的恶化效应是指实际加工处理时间是起始开工时间的线性函数.Jafari等[8]以工件实际加工处理时间是其开工前等待时间呈线性关系为恶化效应的单机调度问题,研究了以最小延迟工件数为优化目标,并运用了分支界定法对问题进行求解.与文献[8]类似,本文考虑的恶化效应调度模型是指实际加工时间与开工前等待时间具有线性不减函数关系.
MapReduce是谷歌公司提出的云计算中具有并行处理的核心计算模型.最初MapReduce源于计算机领域的大数据处理模型,就是在云平台上首先对数据分而治之,即先将大任务分解成许多子任务处理(Map),第2步将这些子任务合起来处理(Reduce).由于生产制造企业里某些工件的加工和大数据处理具有相似之处,因此,本文将该模型拓展并用于制造业中工件的加工调度问题.具体的,MapReduce模型中的工件加工必须经过Map和Reduce两道工序.根据加工调度模型特点作如下陈述[9–11]:1)每个工件的加工需经过两道工序,即Map工序和Reduce工序;2)在第1道工序(Map工序)中,一个工件可以分割成多个任务并行加工,即每个工件可以分割为多个子任务并在多台机器上同时加工;3)当该工件在第1道工序中所有子任务全部加工完成后,方可启动该工件的第2道工序;4)第2道工序(Reduce工序)是一个整合的过程,每个工件只能在一台机器上连续加工直至完成.在实际生活中也能经常遇见关于MapReduce模型的加工制造情形.例如钢丝绳、锚链制造企业.如图1所示,一根粗的钢丝绳由若干个细的钢丝绳合在一起拧成.在Map阶段(第1阶段),若干根细的钢丝绳可以分别在几台机器上同时加工;在Reduce阶段(第2阶段),只能在其中某一台机器上将Map阶段完成的细钢丝绳合成制作为一根粗的钢丝绳.而在实际生产过程中,工件加工具有恶化效应时有发生,其中工件在每个阶段的加工中恶化情形也不相同,因此,这类都是MapReduce模型调度需考虑的影响因素.

图1 钢丝绳制造示意图Fig.1 Schematic diagram of wire rope manufacture
关于MapReduce模型的调度研究已引起国内外学者高度关注,一部分学者研究了MapReduce问题的在线调度算法[9–10],而更多的文献则借助混合整数规划等方法来研究MapReduce模型调度问题.黄基诞等[11]研究了MapReduce模型下具有安装(准备)时间的平行机调度问题,利用改进正余弦算法进行求解.Ling等[12]探讨了MapReduce模型中不同级别的任务,通过建立混合整数规划模型来分析问题.而大部分学者针对MapReduce模型的研究则是关于大数据的处理方面[13–15],即研究大数据在多台PC服务器上加工的时候进行分割(Map)并行处理,然后归拢(Reduce)的一个过程.针对大数据加工处理的调度问题,对数据可以任意大小分割,没有大小限定,而本文是将MapReduce模型与实际生产制造企业相结合,考虑到实际制造企业中的每个工件分割的数量由工件本身属性而定,因此难以做到任意分割.此外,也有学者研究了带任务分割的平行机调度问题[16],建立了混合整数规划模型,并利用分支定界法和差分算法进行求解.
平行机调度问题本身就属于NP难,主要以设计元启发式算法,如遗传算法[1]、正余弦算法[11]、蛙跳算法[17]等为求解思想.其中蝙蝠算法(bat algorithm,BA)是模拟自然界中蝙蝠利用回声定位捕食原理的智能仿生优化算法[18],同时该算法具有数学模型简单、并行处理和收敛速度快等优点,主要用于求解连续函数的优化问题.近期陆续有学者将其拓展用于求离散型方面的优化问题,张文鹏等[19]将蝙蝠算法加入GT算法,同时引入变邻域搜索策略来求解车间调度问题.但是该算法应用集中于流水车间的调度问题[20–21],戚远航等[22]针对多车场车辆路径问题提出一种泰森多边形的离散蝙蝠算法.因此,本文将对该算法的应用进行拓展,用于求解带有恶化效应的MapReduce模型下同类机调度问题.
综上所述,MapReduce模型调度问题与经典的流水车间调度和可拆分平行机调度问题不同,可归纳为:流水车间调度问题一般考虑工件不可分割;而可拆分平行机调度模型中通常假设只有一个工序.但是,在MapReduce模型中,每个工件有两道加工工序,且第1道工序中可将一个工件分割成若干个子任务并行加工.此外,该模型与传统具有恶化效应的同类机调度不同,传统的具有恶化效应的同类机调度问题中,工件加工虽具有恶化效应,但通常一个工件有且只有一个固定恶化加工时间.而MapReduce模型里同一工件上分配在每台机器上的Map子任务大小不同,且Map子任务在各自分配的机器上开工时间也不相同,因此造成不同机器加工同一工件拆分的Map子任务的加工时间具有差异,因此,该模型比经典的具有恶化效应的平行机调度更加复杂,在数学模型建立和算法设计上将会更具挑战.
2 问题建模
2.1 问题描述
假设有M台同类机(每台机器m具有各自加工速度vm,而且加工速度vm与工件类型无关)加工N个工件,工件i的下达(释放)时间为ri,每个工件i均包含Map和Reduce两道工序,其中Map工序包含ni个单位子任务(即Map部分的工件可最多分割为ni个单位子任务),各Map子任务没有严格的先后加工顺序,拆分的Map子任务可同时在不同的机器上加工.每个工件i的Map工序单位子任务正常加工时间长度为Reduce工序正常加工时间长度由于工件的Reduce工序必须在该工件Map工序中所有子任务完成后才可以启动,且只能在一台机器上加工同时工件在该工序中不能分割.工件i实际加工时间是关于开工时间的线性不减函数,工件在Map工序和Reduce工序中的加工时间随着等待时间延长而线性増加,出现恶化效应.因此,为了减少生产中的恶化效应,本文设计一个调度方案以满足所有工件从释放到完成的逗留时间和最小.
此模型主要决策的内容如下:1)Map部分分割的子任务的个数及各个子任务的大小;2)Map部分各子任务在机器上的分配方案;3)Reduce工序在机器上的分配.
2.2 任务分割的优势分析
现通过一个例子来说明任务分割的优势.例如有2台机器处理3个工件(按释放时间排序),为便于描述,假设2台机器加工速度一致vm1,

其中:未进行任务分割的最优调度(见图2),完成时间为33;而进行任务分割的最优调度(见图3),完成时间为26;时间节约7,最后完成时间节约21%.因此任务分割可以有效的提高生产效率.接下来本文将研究的Map任务分割和加工任务分配方案.

图2 未进行任务分割的最优调度Fig.2 Scheduling without task splitting

图3 进行任务分割的最优调度Fig.3 Scheduling with task splitting
2.3 模型假设
问题基于以下基本假设:
1)在任意时刻每台机器只能加工一个Map工序子任务或Reduce工序(即机器同一时刻不能加工两个任务);
2)任何工序在加工过程中均不可中断;
3)每台机器都有各自恒定的加工速度;
4)允许机器在加工过程中出现空闲;
5)在同一台机器上处理同一个工件的同一种任务应连续加工;即同一个工件的同种任务中间不许有其他工件的任务.
2.4 参数符号
本文其他所使用的符号如下: i,j:工件编号;ϕ:机器集合;M为机器的数量;m,k表示机器的编号,k ∈ϕ,ϕ{1,2,···,M};I:工件集合;N为最后一个加工任务;i,j ∈I,I{1,2,···,N};H:Map工序子任务或Reduce工序在机器上的加工位置集合;如果所有的Map工序和Reduce工序都在一台机器上加工,那么位置最多为2N,即H{1,2,3,···,2N};h:Map工序子任务或Reduce工序在机器上的加工位置,h1,2,3,···,2N,h ∈H;ri:工件i的释放时间;αi:在Map 阶段工件i 的恶化系数;βi:在Reduce阶段工件i的恶化系数;vm:机器m的加工速度为vm;L:一个足够大的正数.
2.5 决策变量
以下是决策变量:
1)xh,i,m∈{0,1}:如果工件i的Map工序子任务在机器m上的第h个位置加工,则xh,i,m1;否则为0.
2)yh,i,m:工件i的Map工序在机器m上的第h个位置加工量或子任务数量.
3)zi,m∈{0,1}:如果工件i的Map工序在机器m上加工,则zi,m1;否则为0.
4)Qi,m:工件i的Map工序在机器m上加工的子任务数量.
5)Ri,h,m∈{0,1}:如果工件i的Reduce工序在机器m上的第h个位置执行,则Ri,h,m1;否则为0.
6)δi,m∈{0,1}:如果工件i的Reduce工序在机器m上加工,则δi,m1;否则为0.
13)pi,m:工件i的Map工序恶化加工时间.如果工件i的Map工序子任务在机器m上加工,那么单位任务实际加工时间与其开工前等待时间的长度呈线性递增关系,
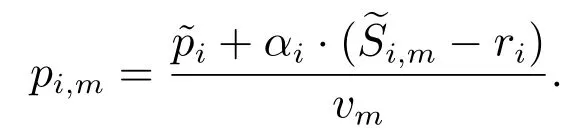

2.6 目标函数
本文考虑的问题模型以最小化所有工件逗留时间和为目标:

在实际生产问题中存在许多MapReduce模型的特性和约束,而本文模型中的约束用数学刻画如下:
处理时间约束:

式(2)表示最大完工时间不小于每个工件的Reduce工序完成时间.式(3)表示工件i的Map工序完成时间必须不早于该工序的每个分割子任务完成时间.式(4)表示工件i的Reduce工序开始时间不得早于Map工序的完成时间.式(5)表示工件i的Reduce工序在同类机m上加工的完成时间和开始时间的关系.式(6)表示工件i的Map工序在同类机m上分配的任务开始加工时间必须大于等于工件释放时间.式(7)表示工件i的Map工序在各同类机m上分配的任务量、加工开始时间与加工结束时间之间的关系.式(8)–(9)表示工件i的Map工序在同类机m的位置h上开始加工时间,必须大于等于前一个位置h −1上加工的Map或Reduce的完成时间.式(10)–(11)表示工件i的Reduce工序在同类机m的位置h上开始加工时间,必须大于等于前一个位置h −1上加工的Map或Reduce的完成时间.式(12)如果工件i的Map工序子任务在同类机m上加工,那么子任务的实际加工时间是关于开工时间的线性不减函数.式(13)如果工件i的Reduce工序任务在同类机m上加工,则实际加工时间是关于其开工时间的线性不减函数.
任务分配约束:

式(14)–(15)表示工件i的Map工序加工机器的选择及加工工作量的相互关系.式(16)–(18)表示工件i的Map工序在机器m上的同一个位置上只加工一次.式(19)表示工件i的Map工序在m机器上的加工量应与该机器上分配的工作量一致.式(20)表示工件i的Map工序工作量等于该工件分配给所有机器的Map工序子任务工作量之和.式(21)–(24)表示工件i的Reduce工序只能在机器m上加工,并且只能加工一次.式(25)表示在机器m的位置h上安排Map工序任务量的上下限约束.式(26)表示在机器m的h位置上只能安排某一工件的一个任务.式(27)表示在平行机m上安排任务的位置是连续的.式(28)表示决策变量的取值范围.
3 蝙蝠算法
本文提出的混合整数规划模型在小数据量算例可以用CPLEX软件进行精确求解,然而在数据规模较大的时CPLEX无法在合理的时间内求取最优解,因此可借助智能优化算法求其近似解.蝙蝠算法(BA)是通过模拟自然界中的蝙蝠利用自身发出声波的响度及脉冲的变化,即利用回声来探测与定位食物位置,从而在飞行中不断的动态改变自己的速度及位置,最终获得食物(最优解)的一种过程.该算法规则主要有4个参数:波频率、飞行速度、响度(音量)以及脉冲发射频度[16–19].这些参数决定了蝙蝠算法寻优速度和精度.
全局搜索:随机飞行蝙蝠的声波频率:

式中: fi表示蝙蝠个体的声波频率;[fmin,fmax]为频率的范围;是一个随机扰动,在[0,1]上服从均匀分布.
蝙蝠的飞行速度:

式中:xi代表蝙蝠在i次迭代的空间位置;x∗为当前空间最优位置.
蝙蝠i的位置移动更新:
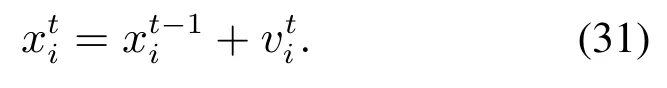
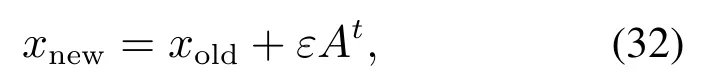
式中: xold为从当前最优解集中随机选择的一个解;rand1是[0,1]内服从均匀分布的随机数;At为当前代蝙蝠的响度;ε为[0,1]上的D维随机向量.
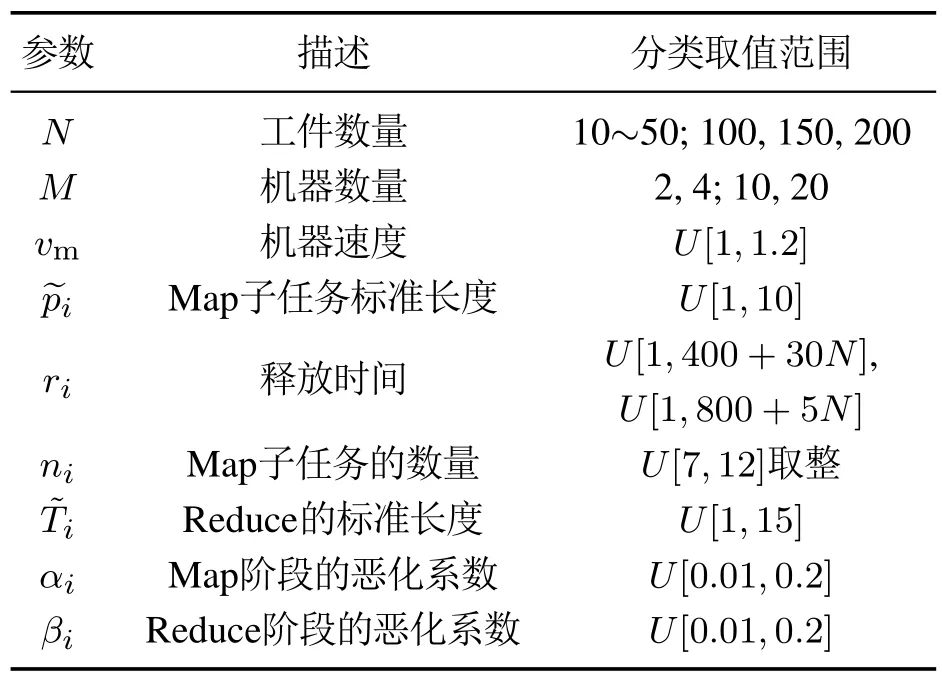
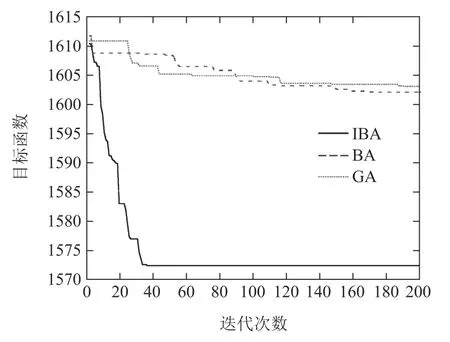
接受新解:通过全局搜索和局部搜索并产生新个体后,如果rand2<,且同时满足函数值也是新解更优f(xnew) 参数调整:当接受新解后,响度A和脉冲频度˜r的将得到更新, 在改进的蝙蝠算法(improved bat algorithm,IBA)的平行机调度中,运用实数编码的位置向量来表示Map工序的分割数量情况和二个阶段的机器调度序列.考虑N个工件和M台同类机,按工件的释放时间ri排序(若释放时间相同,就根据Reduce工序从大到小排序).为便于编程,蝙蝠编码采用至多N(2+M)维实数向量表示N个工件在M台同类机器上加工的调度序列.向量中每一个实数的取值范围是[1,M +1).整个编码分成3个部分:1)前N位的整数部分表示N个工件的Map工序划分的子任务个数;2)接下来的N ·M的实数数字中:整数部分表示Map工序子任务所分配的机器号,小数部分表示Map工序分割部分的大小;3)最后N位的整数部分表示N个工件的Reduce工序对应加工的机器号. 针对随机产生N(2+M)维实数,先分析前N个数(x1,x2,···,xi,···,xN)(其中xi∈[1,M+1)),⌊xi⌋代表每个工件的Map工序划分子任务的个数,表示第i个工件由数量⌊xi⌋台机器来执行.针对部分算列中存在ni 用一个例子说明编/解码的过程.有2台机器处理3个工件,其中3个工件的基础信息见第2.2节中任务分割优势部分. 解码: 1)首先分析前N位数字,根据这N位的整数部分算出每个工件的Map工序被分割的部分.在本算例中有3个工件,因而N3;表1分别可以看出工件1–3的Map工序分割成2个部分; 表1 3个工件2台机器的编码信息Table 1 Code information for 3 jobs 2 machines 这里[·]表示取整.对于工件1,可以得出机器1分配到的Map工序子任务数为2;从而可推算出机器2分配的Map工序子任务数n1−21; BA算法进行局部搜索,步长和响度会随着迭代增加逐渐递减,在这种数值变化趋势下,若缺乏行之有效的变异机制,很容易使种群陷入局部最优.为此,对算法要适当加以改进,采用正余弦扰动增加其寻优能力.表示第t代第i(i1,2,···,N)个个体的位置,当前最好位置个体表示为X∗,正弦余弦扰动数学表达式如下: 其中: t为当前迭代次数;θ ∈[0,2π]为随机参数;ε1,ε2∈[0,1]称为控制参数,是一个随机数,取值的大小会影响算法开发和探索能力. 差分进化算法[23]优点是收敛速度快.能引导群体快速朝最优方向移动,本文在差分进化算法的基础上提出了差分变异策略,如式(36)所示: 本文的正余弦差分扰动策略的步骤如下:选取一个蝙蝠Xb,分别计算出Xc,Xs,Xw比较这些目标函数值,选取扰动中最优的值和当前最优函数值比较,如果扰动后的解更优,则替换X∗.其中这里的选取规则,产生一随机概率p∗∈(0,1),当概率p∗0.1时(即选取数量约为个蝙蝠,NP为种群规模),进行正余弦扰动. 综上所述,求解MapReduce问题的改进蝙蝠优化算法流程可归结如下: 步骤1初始化参数.设定蝙蝠种群规模为NP,脉冲频率的上下限,响度A,最大脉冲率˜r,音量的衰减系数,最大迭代次数为Tmax等参数; 步骤2初始化蝙蝠的初始位置和速度等,计算初始种群的个体适应度值,选择适应度值最优的个体位置作为最优位置; 步骤3根据式(29)–(31)更新脉冲频率、速度和位置; 步骤4产生一随机数rand1,若rand1>ri,则对当前最优蝙蝠位置进行按式(32)扰动得到新的位置,然后比较原解,若适应度更优则替换原位置;否则产生一随机概率p∗∈(0,1),当p∗0.1时按式(34)–(36)进行正余弦差分扰动策略,然后比较原解,若适应度更优则替换原位置; 步骤5产生一个随机数rand2,如果rand2 步骤6若达到终止条件,则输出最优个体,即算法找到的最优解;否则,返回步骤3. 本文提出的算法采用MATLAB 2014a编程,实验运行环境:CPU 2.8 GHz,内存4 GB,Windows 7操作系统(64位).为验证算法寻优性能进行数据仿真试验,当小规模数据算例可用CPLEX 12.5软件进行精确求解;其中本文CPLEX的运行时间上限设置为2 h.而当数据到一定规模时,在规定的时间内无法用该软件进行求解,则运用蝙蝠算法近似求解. 为了评价算法解的质量,本文对问题解的下界进行研究. 定理1假设机器的加工速度v1v2···vM.由于Map工序的子任务可在多台机器上加工,相应的机器数量比较难以确定,故松弛一个条件.假设工件一下达,目前机器都是空闲的,该问题的下界为 证假设工件一下达,目前机器都是空闲的.将该工件的Map工序加工时间平摊到M台机器,那么工件的Map部分加工时间至少为从而推导出Reduce工序的从下达到开始加工这个时间间隔至少为考虑到Reduce工序的恶化效应,把该Reduce工序也交给最快的机器加工,可推出Reduce工序的加工时间至少为从而推出这2个工序的加工时间和该工件的最少逗留时间.显然表达式是目标函数最优解的一个下界. 为了说明改进算法的有效性,评价指标为相对百分比偏差[17](relative percentage deviation,RPD).因此,各类算法所求得的解的质量可用RPD来衡量[17]: 其中: falg是算法alg中计算获得的目标函数值,LB就根据式(37)计算. Time(s):CPU平均运行时间,指算法求得最优解所花费的平均计算时间,算例运行6次,取6次的平均计算时间,以秒(s)为单位. 用传统经典算法遗传算法(genetic algorithm,GA)作比较.算法的参数设定中,GA,BA和IBA的种群数量NP都设定为100,迭代次数200;其中:GA的变异概率pc0.83,BA和IBA设定fmin0,fmax1,A0.25,γ0.05.随机产生算例,算例规模和参数见表2. 对于上述实例用IBA,BA和GA3种算法做实验结果对比.针对不同的机器数量和工件规模,完成了16组实验算例,每个实验算例在同一算法下运行6次.计算出每个算法的评判指标,然后取其平均值.具体运行结果数据列于表3.由于篇幅有限,随机选取N100,M10,αiβi0.05 和N200,M20,αiβi0.05两种情形的算法运行图如图4–5所示. 表2 算例的参数取值范围Table 2 The range of parameters 表3 各算法计算时间比较Table 3 Comparison of computing time of each algorithm 从图4–5分别描绘了最优值的分布.从图中可以看出,迭代初期的时候,各类算法的计算所得目标值基本上相差不大.当达到一定的迭代次数的时候,优化目标无法再改进,而且BA和GA算法有着类似的收敛速度,改进蝙蝠算法IBA有着较为明显的优势,具有更好的收敛性和稳定性. 图4 10台机器100个工件的算法收敛曲线图Fig.4 The algorithm convergence curve of 100 jobs of 10 machines 图5 20台机器200个工件的算法收敛曲线图Fig.5 The algorithm convergence curve of 200 jobs of 20 machines 总之,从图4–5可以看出,改进算法的收敛性与稳定性能优于BA和GA,说明了该改进方法的有效性. 从表3可以看出,工件数量增加一倍时,CPU计算时间并不是相应的成倍增加,而增加的更多.通过16组数据规模的实验,从表4中的第3–6列对应第8–11列可看出,恶化系数越大,恶化越严重,RPD值比较大.第2列的LB1是根据恶化系数αiβi0.05和式(37)计算出来的;而第7列的LB2是根据恶化系数αiβi0.1和式(37)计算出来的.下界值忽略了Map阶段的恶化效应,只考虑Reduce阶段的恶化效应;同时下界随着恶化系数的增加而增加.当工件数量只有10个时,模型可以通过软件CPLEX进行精确求解,精确解比较接近问题的下界,并且其相对偏差RPD都小于5%.当工件数量大于10时,CPLEX软件无法在规定的短时间内求出该问题的精确解.因此只能借助智能算法求得的近似解,问题下界值通过式(37)求得.因为计算RPD的下界值是忽略了Map工序的恶化效应和加工速度差异,故RPD值比较大.但总体低于25%,这说明改进的算法运行性能较好.从图和表中都可以看出,改进蝙蝠算法的数值仿真结果优于GA和基本蝙蝠算法的运行结果,因此,有效验证了改进的蝙蝠算法寻优能力更强.从表中数据看出,RPD值的大小与生成的工件释放流量有关,即与给定机器数量下单位时间内工件释放数量有关.如果在给定的机器数量情况下单位时间内工件释放数量越多(工件释放流量越大),造成工件堆积,来不及加工,等待时间延长,该模型越容易产生恶化效应,RPD值越大.所以50个工件,2台机器的时候,数据显示RPD值最大. 表4 各算法RPD指标比较Table 4 Comparison of RPD indicators of each algorithm 本文探讨了具有恶化效应的MapReduce模型同类机调度问题,建立了混合整数规划模型,设计了改进蝙蝠算法(IBA)进行求解,同时讨论了问题的下界.通过比较发现,RPD值和工件的释放流量大小及恶化系数有关.释放流量越大或恶化系数越大,恶化越严重,则工件在机器间逗留时间越久,RPD值越大.最后,通过数值实验验证了应用改进蝙蝠算法求解MapReduce模型下的同类机调度问题的可行性和有效性.下一步研究考虑从以下几个方面展开:1)是将所设计的算法推广到不确定性的MapReduce调度模型中,如加工时间是一个随机数、区间数或模糊数的情形;2)是探讨考虑能耗的基于Map-Reduce的多目标调度模型.
4 改进蝙蝠算法
4.1 编码方式
4.2 解码方式


4.3 正余弦差分扰动
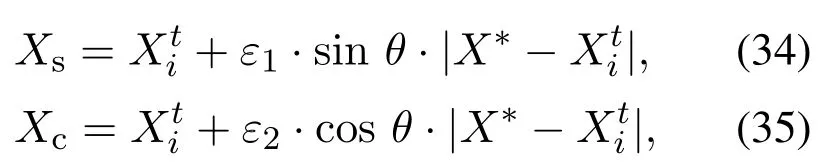
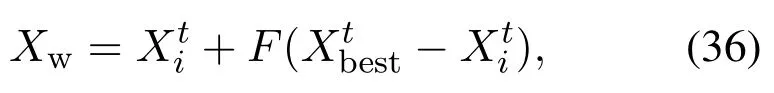
4.4 改进蝙蝠算法流程
5 数值实验
5.1 松弛下界

5.2 评判指标

5.3 实验参数
5.4 实验分析



6 结束语

