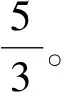带服务器的具有固定序列的平行专用机排序

王超杰，陈光亭，陈 永，张 安

(1.杭州电子科技大学理学院，浙江 杭州 310018；2.台州学院电子与信息工程学院，浙江 台州 318000)

0 引 言

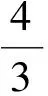
1 问题描述

带服务器的具有固定序列的平行专用机排序问题的定义如下：给定1台服务器，m台平行专用机{M1,M2,…,Mm}和m个不相交的工件集Jk={Jk,1,Jk,2,…,Jk,nk}。其中机器Mk(1≤k≤m)需按照Jk,1,Jk,2,…,Jk,nk的顺序加工工件集Jk。每个工件Jk,j(1≤j≤nk,1≤k≤m)由加载时间Sk,j和加工时间Pk,j组成，其中nk表示第k台机器的工件数，每个工件的加载时间均为1，即Sk,j=1，Pk,j为整数。服务器只对工件进行加载操作，且一次只能对1个工件进行加载。每个工件必须先在服务器加载完毕才能开始加工。对于任意一个可行排序，Ck,nk表示机器Mk上最后1个工件的完成时间，Cmax表示工件的最大完工时间，则Cmax=max{C1,n1,C2,n2,…,Cm,nm}。目标是寻找一个可行排序，使得工件最大完工时间尽可能小，即minCmax。

根据文献[7]的三参数表示法,带服务器的具有固定序列的平行专用机排序问题可表示为PD,S1|fixed-seq,sj=1|Cmax，其中PD表示平行专用机，S1表示一台服务器，fixed-seq表示每台平行专用机加工工件的顺序是固定的，sj=1表示每个工件的加载时间均为1。PD,S1|fixed-seq,sj=1|Cmax是强NP-难的。

2 算法设计与分析

对于问题PD,S1|fixed-seq,sj=1|Cmax，文献[7]提出了MLT算法和MRW算法，其中MRW算法是本文设计改进算法的基础，其基本步骤如下。

(1)对于每台机器Mk，计算当前时刻工件集Jk中未被服务器加载的所有工件的处理时间(包括剩余工件的加载时间和加工时间)，即剩余时间。

(2)服务器完成当前工件上的加载操作后，选择当前时刻最大剩余时间工件集Jk中可被选择的工件进行加载操作；按此规则，直至服务器完成所有工件的加载。

(3)每个工件加载完成后，立刻在机器上加工。

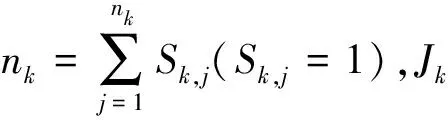
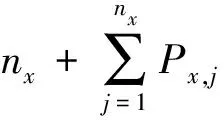
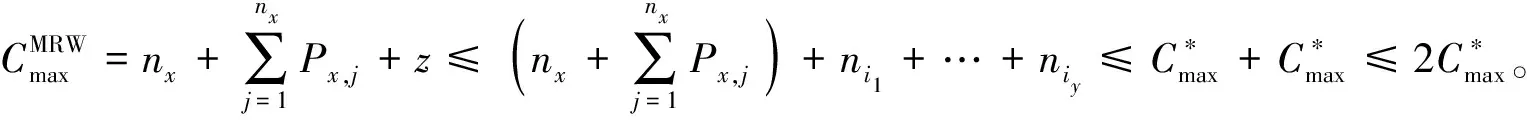
对于PD,S1|fixed-seq,sj=1|Cmax问题的算法设计，一方面要考虑每台机器上工件加工时间总和，另一方面还要兼顾服务器不能有非必要的空闲，从而保证服务器连续工作。为此，本文针对MRW算法进行改进，提出一种平行专用机总加工时间递减的算法(Maximum the Sum of Processing-Time，MSPT)，基本步骤如下。

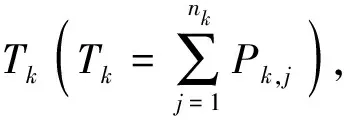
(2)服务器在选择工件进行加载的优先级为J1>J2>…>Jm。零时刻，工件J1,1在服务器上加载。每个工件加载完毕后，服务器从当前剩余的工件序列中，挑选出允许加载的工件集，选择该工件集中优先级最高的工件加载。按此规则，直至服务器完成所有工件的加载。

(3)每个工件加载完成后，立即在机器上加工。

为了便于理解本文提出的MSPT算法，通过一个具体用例来阐述。

m=3时，每个工件的加载时间为Sk,j=1,每个工件的加工时间Pk,j如下：

M1∶P1,1=1;P1,2=1;P1,3=2
M2∶P2,1=1;P2,2=0;P2,3=1
M3∶P3,1=2;P3,2=0;P3,3=1

根据MSPT算法，将服务器加工的工件顺序进行排列并求出MSPT算法所得排序的目标值。

(1)令T1,T2,T3表示对应工件集的加工时间Pk,j之和，

T1=P1,1+P1,2+P1,3=1+1+2=4
T2=P2,1+P2,2+P2,3=1+0+1=2
T3=P3,1+P3,2+P3,3=2+0+1=3

(2)根据平行专用机总加工时间递减的原则，服务器在选择工件进行加载的优先级为J1>J3>J2。零时刻，服务器加载工件J1,1。1时刻，服务器允许加载的工件集为{J2,1,J3,1}，服务器选取J3,1加载；2时刻，服务器允许加载的工件集为{J1,2,J2,1}，服务器选取J1,2加载；重复以上步骤，直至所有工件加载完毕。

(3)每个工件加载完成后，立即在机器上加工。

MSPT算法执行完毕所得的排序，如图1所示。

图1 MSPT算法所得排序

由图1可知，MSPT算法所得排序的目标值为：

证明不妨设T1≥T2≥T3，服务器选择工件进行加载的优先级为J1>J2>J3。设MSPT算法所得排序中，最后完工的工件为Jk,nk(k∈{1,2,3})。按照Jk,nk的归属情况，分成3种情形进行讨论。

情形1k=1，即最后一个完工的工件为J1,n1。

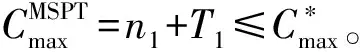
情形2k=2，即最后一个完工的工件为J2,n2。

由MSPT算法可知，J2中的工件在加工时出现空闲的时间段与S1,j有关。再由引理1可知，

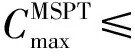
情形3k=3，即最后一个完工的工件为J3,n3。

J3中的工件在加工时出现空闲的时间段与S1,j和S2,j有关。再由引理1可知，

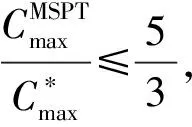
3 结束语