火星车转移坡道柔顺性优化设计及动力学分析
唐 玲,刘 卫,刘金生,危清清
(1.北京邮电大学自动化学院,北京 100876;2.北京空间飞行器总体设计部,北京 100094;3.空间智能机器人系统技术与应用北京市重点实验室,北京 100094)
0 引 言
火星车是承载各种仪器执行火星表面探测任务的重要载体和直接工具。火星车一般不能直接降落在火星表面,需通过着陆器进行搭载,待着陆器软着陆后,通过转移机构将火星车安全转移至火星表面。对于中等重量的火星车,与月球车类似,其转移机构一般由两条坡道组成[1-3]。由于火星地形地貌特征复杂,表面凹凸不平,两条平行的坡道展开和落下后,可能存在较大异面角。当火星车在存在异面角的坡道上行驶时,车轮与坡道护栏会相互挤压,作用力过大,火星车存在侧翻和卡滞等风险。转移坡道关系到火星车能否顺利驶入火星表面,决定了火星车能否成功地开展探测任务。因此,对转移坡道展开优化设计及动力学分析对火星探测任务具有重要实际意义。
目前,有许多关于着陆器机构优化设计和动力学分析的研究[4-8],文献中往往假设着陆器上有一个星球车载荷,而对于提供星球车驶离着陆器的转移坡道的相关研究较少。文献[9-10]介绍了前苏联成功发射的两辆月球车(Lunokhod-1和Lunokhod-2)转移坡道的组成和功能,但没有描述坡道机构设计。文献[11]介绍了嫦娥三号月球车转移坡道的功能设计和试验验证,但没有对坡道机构的性能开展优化设计。文献[12]对日本计划发射的月球车坡道开展了轻量化设计,但是没有考虑坡道异面角的影响。文献[13]考虑了火星局部地形和地貌引起坡道异面角的影响,对坡道长度进行了优化设计,但没有研究火星车与坡道护栏挤压的问题。文献[14]考虑了坡道异面角的影响,坡道设计时增宽了坡道两侧护栏之间的距离,但没有进行动力学分析和验证机构优化设计效果。
综上所述,已发射的转移坡道相关文献主要在机构的功能和组成上进行描述,没有对机构的性能开展优化设计。其他文献主要是针对坡道机构的轻量化和几何尺寸上的优化设计,忽略了两侧坡道异面角会引起的火星车与坡道护栏作用力过大,可能会造成的火星车卡滞和侧翻等风险。针对这一问题,本文拟对一种抽展式转移坡道开展柔顺性优化设计和动力学分析,设计坡道的间隙机构和限位机构,计算机构关键设计参数的最优值,以自适应调整两侧坡道的距离,减小火星车与坡道护栏之间的相互作用力,并通过动力学仿真验证优化设计的有效性。
1 火星车坡道转移原理
为了便于分析,定义着陆器坐标系(O-XYZ)为全局绝对坐标系,坐标系原点O位于着陆器平台上表面的几何中心;X垂直于着陆器平台的表面,向上为正;Z轴与着陆平台上的坡道平行,延坡道展开方向为正;Y轴方向根据右手定则确定,如图1所示。

图1 全局坐标系定义Fig.1 The definition of global coordinate system
抽展式转移坡道工作过程为:①坡道在发射段、地球-火星轨道转移段、着陆段处于折叠压紧状态;②待着陆器安全着陆在火星表面后,根据着陆区域地形地貌,坡道沿着地势平坦的一侧展开;③当坡道抽展到位后,在抽展机构驱动力和坡道自身重力下,坡道向下旋转至接触火星表面,形成供火星车转移的通道;④火星车通过坡道从着陆平台驶入火星表面。
转移坡道由-Y和+Y两侧坡道组成,分别简称为坡道1和坡道2。坡道延同一轴线展开后,由于火星的地形地貌特征复杂,坡道1和坡道2末端接触地面的高度不相同,会产生一个异面角度φ,如图2(a)所示。火星车的差速和悬架机构仅能保证车体前后倾斜角度较小,不能避免车体的侧向倾斜。随着火星车距离地面越近,车体侧向倾斜角度越大,两侧车轮之间在XY平面的投影距离越小,而两侧坡道的距离在XY平面投影始终不变,如图2(b)所示,其中,A1~A3分别表示为火星车-Y测车轮在坡道1顶端、中部和末端的位置;B1~B3,分别表示为火星车+Y车轮在坡道2顶端、中部和末端的位置。从图2中可以看出火星车在下坡道的过程中,车轮与坡道内侧护栏相互挤压,容易引起坡道变形、车轮被挤出导轨,甚至火星车翻车等风险。

图2 火星车下坡道过程的构型Fig.2 Configuration during the descent of the rover
为了提高火星车通过坡道转移的稳定性和可靠性,需要两侧坡道距离有一定的调整功能。常规的方法是采用电机驱动的方式使坡道顶端具有绕内外侧旋转的功能,但是坡道期望的旋转角度随着着陆地形的不同而不同,同时对电机的控制精度要求较高,该方法大大增加了坡道系统的复杂性和不确定性。本文拟设计坡道的间隙机构和限位机构,来增加坡道的柔顺性,以实现两侧坡道距离的自适应调整功能。
2 坡道机构柔顺性优化设计
2.1 间隙机构设计方案
在坡道与着陆平台连接的根部设计间隙机构,使两侧坡道距离具有自适应调节的功能。间隙机构的自适应调节功能原理如图3所示。在间隙机构上表面,均布4个导轮,为坡道的抽展提供直线滚动约束和调整间隙。坡道仅受挂钩点位置约束,当导轮与坡道存在间隙时,坡道可以在导轮槽中进行一定角度的摆动。两侧坡道间的距离会随着外力作用增大或减小。

图3 间隙机构原理Fig.3 The principle of clearance mechanism
2.2 限位机构设计方案
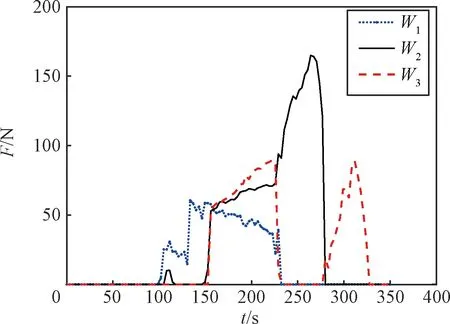
坡道限位机构功能原理如图4所示,图4(a)和图4(b)分别为两侧坡道无异面角工况和两侧坡道有异面角工况的示意图。其中,限位机构由1个限位杆和2个球关节组成。限位杆的作用是限定两坡道连接距离不变,球关节仅约束限位杆两端位置,不约束限位杆两端的姿态。d1和d2分别为两种工况下,两侧坡道的距离在YZ平面的投影距离。当两侧坡道摆转过程不存在异面角时,坡道之间的距离保持不变,始终为d1;当两侧坡道摆转过程存在异面角时,由于限位杆距离的限制,使两侧坡道末端之间的距离保持不变,而YZ面的投影距离缩小为d2(d2 图4 限位机构原理Fig.4 The principle of limit mechanism 两侧坡道距离的调整量需要与火星车的行驶状态相匹配,间隙机构的间隙设计过小,会造成火星车与坡道护栏相互挤压;限位杆的安装位置设计不合理,会导致坡道可调整的范围不足。本节建立坡道的运动学模型,计算和分析间隙机构与限位机构关键设计参数的最优值。 定义坡道坐标系如图5所示,O1、O2分别为坡道1和坡道2转轴坐标系,坐标系原点过坡道转轴,位于坡道护栏中心,Z1、Z2方向分别为坡道1和坡道2的旋转轴方向。O0为零位坐标系,原点位于O1和O2两点的中点,O0坐标系各轴的方向与着陆器坐标系O的方向相同。O3和O4原点分别位于坡道1和坡道2挂钩点,Z3和Z4的方向为坡道1和坡道2的摆转方向。O5和O6原点分别位于坡道1和坡道2限位杆球关节中心。O7和O8原点分别位于坡道1和坡道2的末端。O5~O8初始时刻坐标系方向与O1相同。两侧坡道坐标系间的尺寸参数相同,表示为a1~a5。β1和β2分别为坡道1绕Z1轴的转角和坡道2绕Z2轴的转角,β3和β4分别为坡道1绕Z3轴的转角和坡道2绕Z4轴的转角。 图5 坡道坐标系Fig.5 The coordinate system of ramps (1) 根据式(1),可以得出坐标系Oj与相邻坐标系Oi的位移和旋转矩阵如式(2)和(3)所示。 (2) (3) 限位机构球关节之间的位移矢量P5,6和距离L可表示为式(4)所示。 (4) 式中:P0,5和P0,6分别为坐标系O5和O6在O0坐标系下的位置矢量。根据式(2)和式(3)可以得出P0,5和P0,6表达式如式(5)所示。 (5) 同理,两侧坡道末端的位移矢量P7,8和距离Lm可以表示为式(6)所示。 (6) 基于以上推导的运动学模型,以两侧坡道最大异面角φ=8°,限位杆在坡道上的安装空间a4=0.10 m,坡道长度l=2.89为约束条件,两侧坡道距离与火星车两侧车轮的距离相同为优化目标,计算两侧坡道的最大摆转角、间隙机构的间隙,以及限位杆端点O5和O6的最优安装位置。 设坡道尺寸参数a1=0.60 m,a2=0.09 m,两侧坡道长度相等,统一用l表示,l=a2+a3+a5。φ=8°,β1=β2=0°时,l从0增加到2.89 m,根据式(6)可以得出Lm与l的关系曲线,如图6所示。从图中可以看出,当两侧坡道存在异面角时,Lm随着l的增加而增加,Lm由1.2 m增加到1.27 m,而火星车两侧车轮的距离始终保持1.2 m,因此,需要坡道末端至少具有0.07 m的调整距离。 图6 Lm与l的关系Fig.6 The relationship between Lmand l 假设由于限位杆的作用两侧坡道均向坡道内调整,摆转角度相同,设摆转角β=-β1=β2。φ=8°时,根据式(6),可以得出Lm随着β的变化情况,如图7所示。从图中可知,当β越大,Lm越小;当β=0.8°时,Lm缩小为1.2 m,与火星车两侧车轮的距离相同。因此,设置0.8°为两侧坡道的最大摆转角。 图7 Lm与β的关系Fig.7 The relationship between Lm and β 间隙机构间隙调整原理如图8所示,根据机构的几何关系得出式(7)所示的关系式。 δ=k-b (7) 式中:δ为间隙机构的间隙;b为坡道的宽度;h为纵向两导轮的轴线距离;k为横向两导轮的轴线距离;且k满足式(8)的几何关系。 (8) 设定b=0.05 m,h=0.01。当β=0.8°时,根据式(7)和式(8)计算得出,δ=0.0014 m,k=0.0514 m。 图8 间隙调整原理Fig.8 The principle of clearance adjustment 当φ=8°,β=0.8°时,根据式(4),可以计算出L与l的关系,曲线如图9所示。从图中可以看出:l=0 m时,L=1 m;L随着l的增大,呈现出先降低后增大的非线性变化;l=2.6 m时,L=1 m。因此,长度为1 m的限位杆安装在l=2.6 m处,可以满足φ≤8°的调整需求。 图9 L与l的关系Fig.9 The relation between L and l 综上计算和分析得出,间隙机构和限位机构关键设计参数的最优设计值为:两侧坡道的最大摆转角为0.8°,间隙为0.0014 m;限位杆端点O5相对于O3的最优安装位置为(2.6,0.1,0)m,端点O6相对于O4的最优安装位置为(2.6,-0.1,0)m。 本节基于ADAMS软件建立火星车和坡道的动力学模型,对坡道下落过程和火星车在坡道上的行驶过程进行动力学仿真,验证坡道柔顺性的优化效果。 火星车和坡道的动力学仿真模型中包含的要素包括:①火星车的多柔体动力学模型;②地面模型;③坡道模型:坡道的几何模型,间隙机构模型,限位机构模型等。动力学模型的可视化界面,如图10所示。模型中,火星重力加速度设置为3.72 m/s2;火星车车轮与平台、坡道和地面的接触模型均采用contact面接触模型,设置车轮与坡道的接触刚度为30000 N/mm,阻尼为30 N/(mm·s-1),静摩擦系数为0.1;车轮与地面的接触刚度为2000 N/mm,阻尼为1 N/(mm/s),静摩擦系数均为0.3;火星车的车轮的行驶速度为5.25 (°)/s。 图10 动力学模型的可视化界面Fig.10 The visual interface of the dynamic model 本节分别对两侧坡道异面角φ为0°、4°、8°的三种典型工况下坡道下落过程及火星车驶离坡道过程进行仿真,设置β1=-22°,β2=β1+φ。坡道下落过程仿真时长设置为90 s,步长为0.05 s。火星车在坡道上行驶过程仿真时长350 s,步长0.05 s,t=25 s时刻火星进入坡道,t=335 s时刻火星车完全驶离坡道,进入火星表面。对作用力数据采用二阶巴特沃斯低通滤波器滤波,归一化频率为0.04 Hz。 仿真结果如表1所示,其中,Fbm和Flm分别为坡道优化前和优化后,火星车在坡道上行驶过程中火星车与坡道护栏的最大作用力。R为Flm相对于Fbm减小的百分比。Lmy为两侧坡道末端的距离Lm在YZ平面的投影距离。从表中可以看出:两侧坡道异面角φ=0°时,采用优化前和优化后的坡道,Fbm=Flm,Lmy=0;采用优化前和优化后的坡道,Fbm、Flm和Lmy均是随着φ的增加而增大;φ越大,R越大,说明优化后的坡道对火星车与坡道护栏的作用力改善越明显。 表1 仿真结果Table 1 The simulation results 选取φ=8°的工况对仿真结果进行详细讨论与分析。 坡道在抽展后下落过程中,Lmy随时间的变化曲线如图11所示,从图中可以看出优化前的坡道Lmy始终为1200 mm;优化后的坡道Lmy逐渐减小,由1200 mm缩小至1130 mm,调整了70 mm。由于坡道2在t=48 s时,接触到地面,Lmy在该时刻产生一个波动。 图11 坡道下落过程中的LmyFig.11 Lmy during ramps descent 使用优化前的坡道转移火星车时,火星车与坡道护栏最大作用力位于+Y侧车轮,+Y侧车轮与坡道护栏作用力曲线如图12所示,图中t为仿真时间,Wi(i=4~6)表示火星车+Y侧的3个车轮。从图中可以看出火星车进入坡道后,在t=150 s左右,车轮与坡道护栏接触,车轮与坡道护栏最大作用力为270 N。 图12 火星车+Y侧车轮与坡道护栏作用力曲线Fig.12 Force curve of +Y-side wheels of the rover and the ramp guardrails 使用优化后的坡道转移火星车时,火星车与坡道护栏最大作用力位于-Y侧车轮,火星车车轮与坡道护栏作用力曲线的计算结果如图13所示。从图中可以看出火星车进入坡道后,在t=98 s左右开始与坡道护栏接触。当两侧坡道存在异面角时,由于优化后的坡道会自适应减小两侧坡道的距离,相对优化前的坡道,火星车与坡道护栏接触的时间更加靠前。火星车-Y侧车轮与坡道护栏最大作用力为165 N。相对于坡道优化前,采用优化后的坡道,火星车与坡道护栏最大作用力由270 N降到165 N,作用力减小39%。 图13 火星车-Y侧车轮与坡道护栏作用力曲线Fig.14 Force curve of -Y-side wheels of the rover and the ramp guardrails 本文对一种抽展式火星车转移坡道开展柔顺性优化设计和动力学分析,得出如下结论: 1)间隙机构和限位机构关键设计参数的最优设计值为:两侧坡道的最大摆转角为0.8°,间隙为0.0014 m;限位杆端点O5相对于O3的最优安装位置为(2.6,0.1,0)m,端点O6相对于O4的最优安装位置为(2.6,-0.1,0)m; 2)优化后的坡道柔顺性大幅提高,坡道可以自适应调整两侧的距离,两侧坡道的异面角φ越大,调整的距离越大。在φ=8°时,优化后的坡道相对于优化前的坡道,Lmy缩小了70 mm; 3)两侧坡道的异面角φ越大,优化后的坡道对火星车与坡道护栏的作用力改善越明显。在φ=8°时,采用优化后的坡道,使火星车与坡道护栏作用力减小39%。 以上仿真和分析结果说明采用柔顺性优化后的坡道可以有效降低火星车与坡道护栏的作用力,实现火星车在坡道上的安全行驶。
2.3 关键设计参数的最优值计算

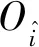



3 动力学分析与验证




4 结 论

