复合材料人形杆压扁过程数值模拟分析

杨 慧，刘 恋，刘荣强，刘永斌

(1.安徽大学电气工程与自动化学院，合肥 230601；2.哈尔滨工业大学机器人技术与系统国家实验室，哈尔滨 150080)

0 引 言

超弹性杆主要应用于大型空间可展天线和太阳帆的支撑背架、探测臂等，展开可靠性高[1-5]。展开机构在发射过程中处于折叠收拢状态并固定在运载火箭内，体积最小，待发射入轨后逐渐展开成为一个大型复杂的宇航结构，锁定并保持为工作状态[6]。

美国国家航空航天局(NASA)[7]研制出 15 m 口径环状展开天线，由一个可伸展三棱柱和可展开桁架组成，反射面由拉索固定，其展开可靠性较高，但刚度较差。美国喷气推动实验室提出一种 2.2 m 边长的矩形薄膜天线机构[8]，充气式薄膜天线收拢体积小、质量轻，但形面精度不易保证，空间环境对天线结构的影响较大。超弹性截面形状主要有圆形杆(STEM)、豆荚杆和人形杆，德国航空航天中心提出一种豆荚杆驱动的薄膜SAR机构[9]，该豆荚杆是一种双凸面超弹性杆，可缠绕弯曲收拢成一卷，豆荚杆为薄膜展开提供驱动力，通过电动机控制展开速度，此类天线具有体积小、展开可靠性高等优点，但应力集中明显。

在国内，李瑞雄等[10-11]采用静力学对缠绕肋压扁缠绕过程进行了研究，确定了4层铺层方式并对每层的应力等特征分析总结。丁峻宏等[12]采用显示动力学对豆荚杆的压扁缠绕以及展开过程进行了非线性数值模拟分析。邹涛等[13]针对空间可展薄膜阵面天线的透镜式薄壁复合材料分别采用了拉扁和压扁两种方法研究了拉伸力、应力等特征。张展智等[14]对不同方式卷曲的空间伸展臂进行展开过程仿真并通过试验验证。

人形杆是由两个横截面具有一定曲率的薄壁壳体粘贴在一起组成的，压扁后可实现人形杆的卷曲缠绕。由于其横截面的特殊性，相比于同类结构展开状态刚度更高。利用ABAQUS软件进行仿真，对人形杆复合材料对称铺层与反对称铺层方式、铺层角度的影响以及在不同复合材料下压扁过程的应力变化规律进行数值分析，从压扁过程中材料受力特点对材料铺设情况进行研究，确定有效的数值模拟分析方法，并得到最佳材料铺设方式。

1 几何模型及材料参数

人形杆横截面形状如图1所示，由碳纤维环氧树脂复合材料T300、T800按照不同的铺层方式构成，复合材料参数如表1所示。人形杆的初始状态是完全展开的，在人形杆左、右两侧分别设置一个压块，两个压块向中间运动使人形杆两面逐渐接触，接触由点、线逐渐扩展为面，人形杆本身处于弹性小应变阶段，去除约束后可恢复其横截面初始形状。

以人形杆水平粘接段的端点为原点建立坐标系，人形杆横截面关于xoz平面对称，材料单片厚度t1=0.5 mm，粘接段宽度为ω=40 mm，总厚度是t2=1.1 mm，横截面半径是R=153 mm，弯曲角度为θ=85°；采用两个平板压块对人形杆进行压扁，压块沿人形杆横截面y轴方向长度为400 mm，沿人形杆横截面z轴方向宽度为200 mm，分别在两个压块几何中心建立两个参考点，作为压块的控制点并定义刚体约束；创建一个Cohesive部件模拟人形杆粘接段，粘接段尺寸为40 mm×1000 mm。

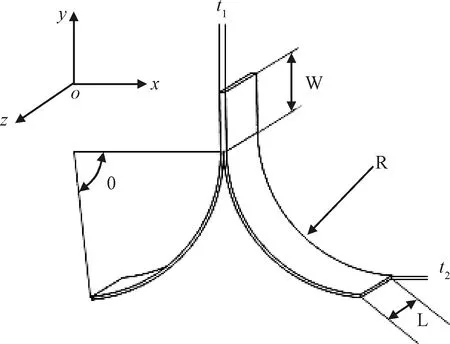
图1 人形杆截面形状Fig.1 Cross-section of TRAC boom

表1 人形杆复合材料参数Table 1 Material parameters of TRAC boom

人型杆上、下两片每层厚0.125mm，复合材料采用4层铺层方式，4种不同铺层角度的铺层方式如图2所示，各层材料的主轴方向沿轴1方向。

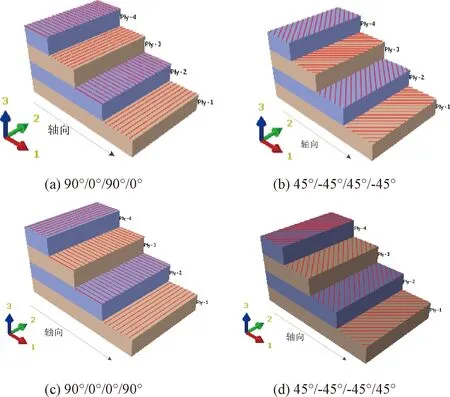
图2 人形杆各层材料铺设布置图Fig.2 Ply lay-out of TRAC boom material

2 有限元模型

采用ABAQUS建立三维有限元模型，两压块均设置为解析刚体模拟，压块作为主面与人形杆之间建立接触；Cohesive部件与人形杆粘接段采用绑定连接，粘接段整体完全固定；人形杆弯曲部分上、下内表面建立接触，避免人形杆产生穿透；模拟压扁过程中压块与人形杆的接触由线逐渐扩展为面，直至全部接触，实现人形杆横截面完全压扁。人形杆采用壳单元S4R模拟，粘结胶采用表面单元C3D8R模拟。为了实现压扁，人型杆弯曲段布置了较密的种子，而中间粘接段部分单元网格划分较稀疏，整个人型杆分为20000个单元。

人形杆关于xoz平面成轴对称，新建一个路径，选取1/2杆宽对称处横截面进行数值特征分析，如图3所示。

图3 人形杆分析截面及单元Fig.3 The section and element of numerical analysis along TRAC boom

3 结果分析

3.1 同种材料铺层

仿真模型以T800为铺设材料，共铺设4层，分析不同铺设角度对应力影响情况。

3.1.1反对称层合板

1)[90°/0°/90°/0°]铺层

图4(a)为压块向下移动40mm时，以[90°/0°/90°/0°]方式铺设上半部第一层沿分析横截面应力大小分布曲线。由图4(a)可知，在粘接段与圆弧段连接处的等效应力、S11应力达到最大，分别是41.7 MPa和42 MPa。人形杆粘接段S11应力值与等效应力值接近于零。圆弧段主要受到压块下压力作用，产生压应力，S11的值为负。图4(b)为压扁后沿分析横截面各层的等效应力。由图可知，人形杆圆弧段应力分布较均匀，圆弧段与粘接段连接处应力最大，第一、二、三和四层的最大等效应力分别是133.4 MPa、1.8 MPa、143.8 MPa和17.1 MPa，第一、三层(铺层角度为90°)等效应力明显大于第二、四层(铺层角度为0°)等效应力。

图4 [90°/0°/90°/0°]铺层应力曲线Fig.4 Stress curve of laying [90°/0°/90°/0°]

2)[45°/-45°/45°/-45°]铺层

采用[45°/-45°/45°/-45°]铺层方式时的有限元模型尺寸和设置与[90°/0°/90°/0]铺层时完全一致，图5(a)为压块向下移动40 mm时人形杆上半部第一层沿分析横截面的应力曲线。由图5(a)可知，在粘接段与圆弧段连接处的等效应力、S11应力达到最大，压扁后沿分析横截面各层的等效应力如图5(b)所示，圆弧段与粘接段连接处应力较大，第一、二、三和四层的最大等效应力分别是68.2 MPa、30.1 MPa、66.2 MPa和75.6 MPa，每层分布规律相同，在粘接段与圆弧段连接处产生应力集中，然后逐渐趋于稳定。第一、三层(铺设角度为45°)和第二、四层(铺设角度为-45°)等效应力相近，变化趋势相同。

图5 [45°/-45°/45°/-45°]铺层应力曲线Fig.5 Stress curve of laying [45°/-45°/45°/-45°]

3.1.2对称层合板

1)[90°/0°/0°/90°]铺层

图6(a)为压块向下移动40 mm时人形杆上半部第一层沿分析横截面的应力曲线，图6(b)为人形杆以[90°/0°/0°/90°]铺设方式压扁后沿分析横截面各层的等效应力。第一、四层铺设角度相同，等效应力分布规律也相同，粘接段等效应力最小，圆弧段与粘接段连接处应力最大，第一、四层的最大等效应力分别是233 MPa和 362 MPa，圆弧段等效应力变化比较平稳，逐渐趋向于零；第二、三层的最大等效应力是5 MPa，远小于第一、四层等效应力。

图6 [90°/0°/0°/90°]铺层应力曲线Fig.6 Stress curve of laying [90°/0°/0°/90°]

2)[45°/-45°/-45°/45°]铺层

人形杆采用[45°/-45°/-45°/45°]方式铺设，压块向下移动40mm时人形杆上半部第一层沿分析横截面的应力曲线如图7(a)所示，压扁后沿分析横截面各层的等效应力如图7(b)所示。圆弧段与粘接段连接处应力较大，第一、二、三和四层的最大等效应力分别是73.3 MPa、13.5 MPa、27.4 MPa和110.3 MPa，第四层(最外层)和第一层(最内层)应力较大，第二层和第三层(中间层)应力较小，最外侧和最内侧分别处于拉伸和压缩状态，等效应力大于第二、三层。

由图6(b)与图7(b)可知，在对称层合板中，[45°/-45°/-45°/45°]铺层中的最大等效应力小于[90°/0°/0°/90°]铺层的最大等效应力。

同种材料不同角度铺层方式下，人形杆横截面最大等效应力如表2所示，由表可知：不同铺层方式的人形杆最大等效应力由大到小进行排列，分别是[90°/0°/0°/90°]、[90°/0°/90°/0°]、[45°/-45°/-45°/45°]和[45°/-45°/45°/-45°]。其中铺层角度为[90°/0°/90°/0°]与[90°/0°/0°/90°]的应力曲线规律类似，均是与90°对应的层应力较大，与0°对应的层较小；[45°/-45°/45°/-45°]和[45°/-45°/-45°/45°]应力曲线规律类似，均是第四层和第一层应力较大，第三层和第二层应力较小。

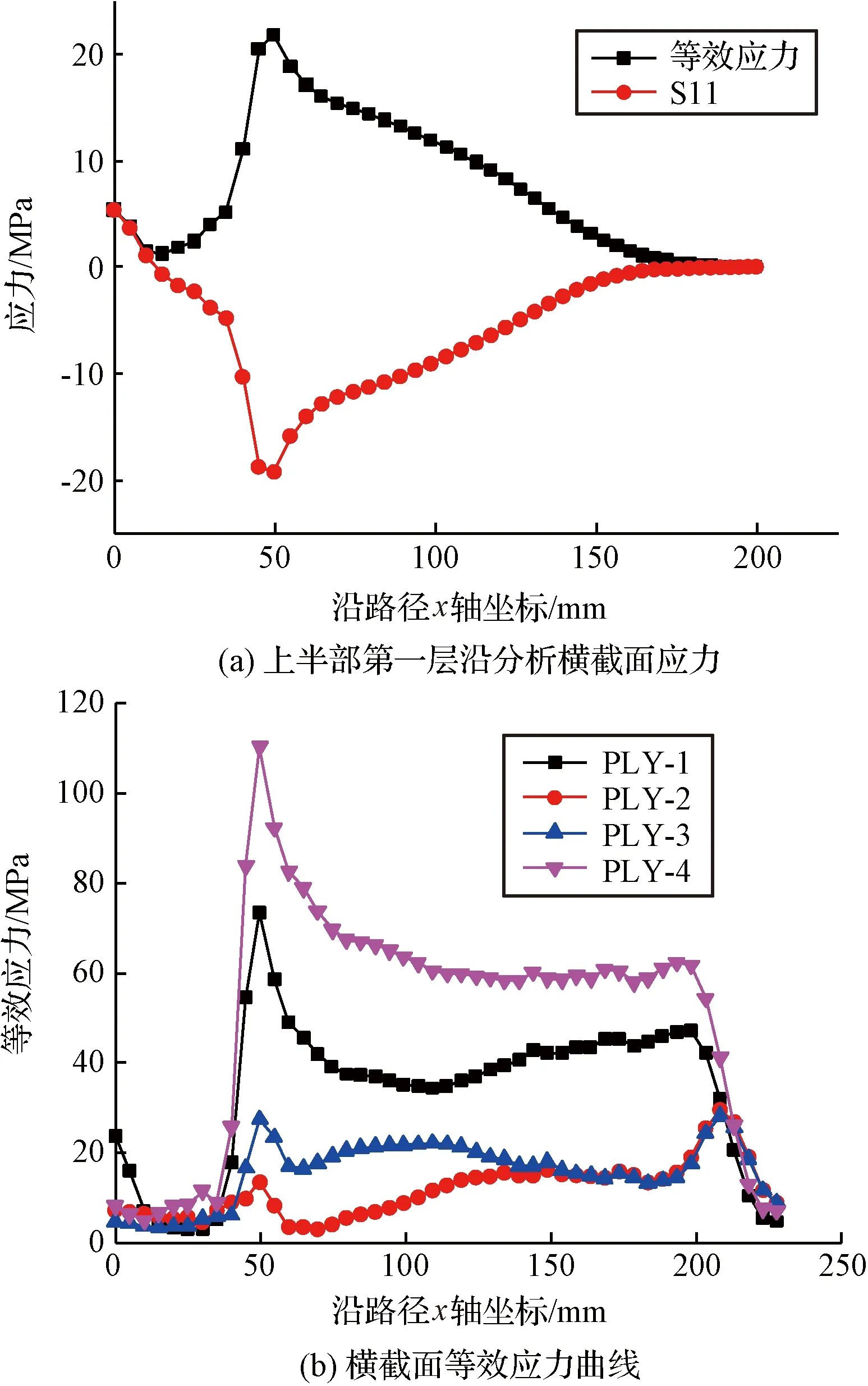
图7 [45°/-45°/-45°/45°]铺层应力曲线Fig.7 Stress curve of laying [45°/-45°/-45°/45°]

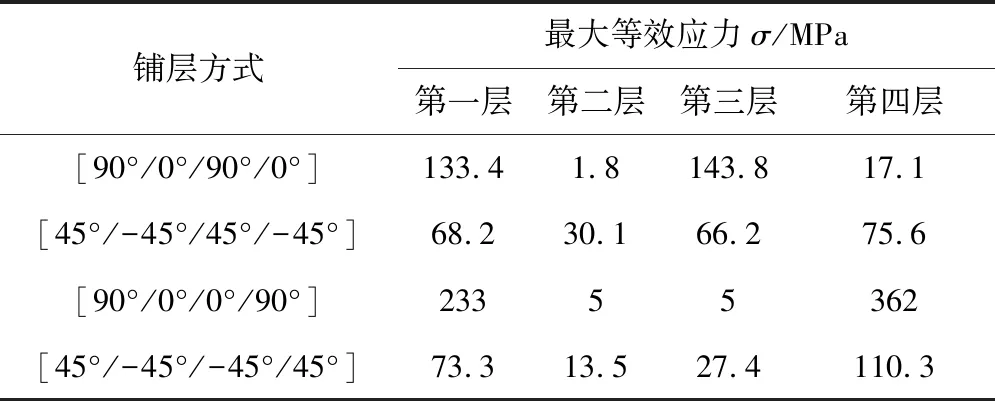
表2 同种材料下的人形杆横截面最大等效应力Table 2 Maximum mises stress of the cross section under the symmetric same materidal

对比图4至图7可知：在[90°/0°/90°/0°]与[90°/0°/0°/90°]铺层方式中，相同的角度对应的应力变化规律相似，90°层等效应力远大于0°层等效应力，铺设角度对等效应力影响较大，铺层位置对等效应力影响较小；在[45°/-45°/45°/-45°]和[45°/-45°/-45°/45°]铺层方式中，均是第四层和第一层应力较大，第三层和第二层应力较小，铺层位置对每层应力影响较大，铺层角度对应力的影响较小。

3.2 不同材料铺层

通过3.1的结果比较与分析，得到人形杆以同种材料铺设压扁后两种应力较小的铺层方式，分别是[90°/0°/90°/0]和[45°/-45°/45°/-45°]铺层方式，讨论这两种铺层方式在不同的铺层材料下等效应力变化规律。

3.2.1T300/T800/T300/T800

分别采用T300和T800两种复合材料对人形杆进行铺层，材料参数如表1所示，每层材料种类依次改变，如表3所示。

表3 铺设材料与层数的关系Table 3 The relationship between laying material and number

1)[90°/0°/90°/0°]铺层

以[90°/0°/90°/0°]方式铺层，人形杆完全压扁后沿分析横截面各层的等效应力分别如图8所示，应力较大层的角度为90°，应力较小层的角度为0°。

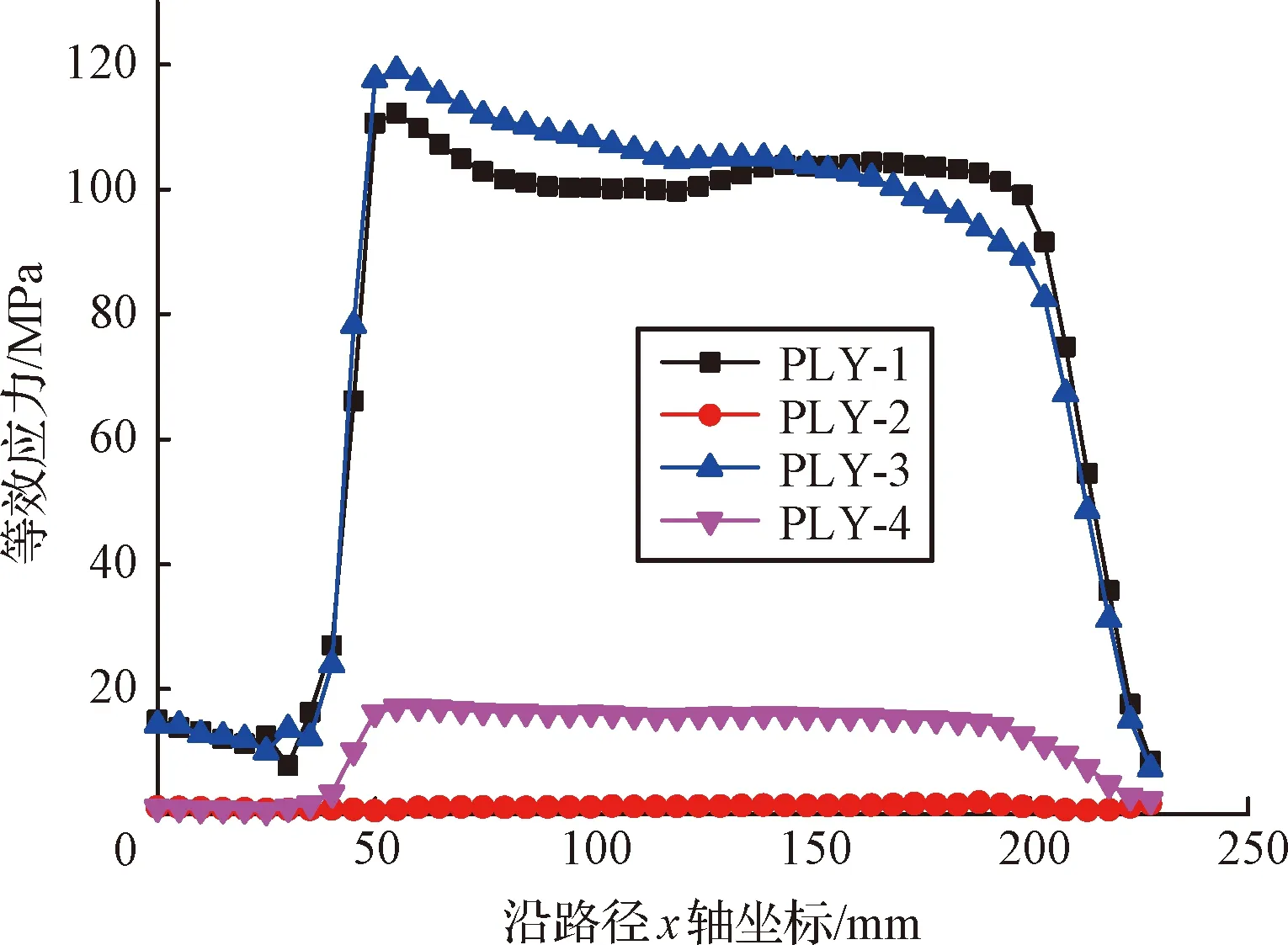
图8 横截面等效应力曲线Fig.8 Mises stress of the top half TRAC boom

2)[45°/-45°/45°/-45°]铺层

以[45°/-45°/45°/-45°]方式铺层，人形杆完全压扁后沿分析横截面各层的等效应力分别如图9所示。圆弧段与粘接段连接处应力较大，第一、二、三和四层的最大等效应力分别是62.2 MPa、30.8 MPa、59.8 MPa 和76.2 MPa。

图9 横截面等效应力曲线Fig.9 Mises stress of the top half TRAC boom

3.2.2T800/T300/T800/T300

分别采用T800和T300两种复合材料对人形杆进行铺层，每层材料种类依次改变，如表4所示。

表4 铺设材料与层数的关系Table 4 The relationship between laying material and number

1)[90°/0°/90°/0°]铺层

压扁后沿分析横截面各层的等效应力如图10所示，圆弧段与粘接段连接处应力较大，第一、三层分布规律相同，在粘接段与圆弧段连接处产生应力集中，然后逐渐趋于稳定。

图10 横截面等效应力曲线Fig.10 Mises stress of the top half TRAC boom

采用两种材料和一种材料以[90°/0°/90°/0°]方式铺设压扁后的等效应力变化规律完全相同，每层最大等效应力变化情况如表5所示。由表可知，采用两种材料以[90°/0°/90°/0] 方式铺设压扁后的最大等效应力(除第四层保持不变)均降低，其中第二层降低的幅度最大。采用T800/T300/T800/T300材料压扁后第一、三层等效应力大于采用T300/T800/T300T/T800材料压扁后第一、三层最大等效应力，第二、四层最大等效应力相等。

表5 人形杆横截面最大等效应力Table 5 Maximum mises stress on cross section

2)[45°/-45°/45°/-45°]铺层

人形杆采用[45°/-45°/45°/-45°]方式铺设，压扁后各层的等效应力如图11所示，圆弧段与粘接段连接处应力较大，第一、二、三和四层的最大等效应力分别是65.7 MPa、27.4 MPa、63.7 MPa和71.4 MPa。

图11 横截面等效应力曲线Fig.11 Mises stress of the top half TRAC boom

采用两种材料和一种材料以[45°/-45°/45°/-45°]方式铺设压扁后的等效应力变化规律完全相同，每层最大等效应力变化情况如表6所示。

由表6可知，采用两种材料以[45°/-45°/45°/-45°]方式铺设压扁后的每层最大等效应力均降低，其中第二层降低的幅度最大。采用T800/T300/T800/T300材料铺设，压扁后第一、三层等效应力大于采用T300/T800/T300/T800材料铺设压扁后第一、三层等效应力，第二、四层等效应力小于采用T300/T800/T300/T800材料以[45°/-45°/45°/-45°]方式铺设压扁后第二、四层等效应力，在变化幅度上，采用T800/T300/T800/T300材料进行铺层，等效应力的变化幅度小于以T300/T800/T300/T800材料铺层的等效应力变化幅度。

表6 人形杆横截面最大等效应力Table 6 Maximum mises stress on cross section

4 结 论

采用ABAQUS/Explicit法对复合材料人形杆的压扁过程进行了仿真，得到以下结论。

1)人形杆采用同一复合材料T800以对称和反对称两种方式铺层，共铺设四层，完全压扁后两种应力较小的铺层方式分别是[-45°/45°/45°/-45°]和[45°/-45°/45°/-45°]，两种不同角度铺层应力曲线变化规律相似，均是第一、四层应力较大，第二、三层应力较小，与铺层角度的正负无明显关系。

2)在两种材料中，对应力较小的两种铺层方式T300/T800/T300/T800和T800/T300/T800/T300进行分析，得到采用T800/T300/T800/T300铺层顺序和[45°/-45°/45°/-45°]的铺层角度时，其结构的应力较小，是一种较佳的人形杆铺设方式。