铺层参数对复合材料电池箱盖模态和稳定性的影响
刘传波,陈傲杰,王稳,肖洒
(1.武汉理工大学机电工程学院, 湖北武汉 430070;2.湖南三合汽车新材料有限公司,湖南长沙 410323)
0 引言
随着社会环保意识不断增强,我国对新能源汽车的政策支持不断增加,新能源汽车的生产规模不断壮大,但目前电池储存的能量受到限制,续航里程不足、整车成本高,严重阻碍新能源汽车发展。轻量化成了解决续航里程的重要手段之一。纤维增强复合材料汽车零部件由于密度低、比强度高、耐腐性强等特点成为汽车零部件的主要发展方向。赵晓昱和张树仁[1]利用刚度等效设计方法,用复合材料代替金属材料对电池盒进行轻量化设计。HARTMANN等[2]通过有限元软件对电池箱的结构进行了优化设计,不仅提高电池箱的固有频率,而且将质量降低了20%。对于复合材料而言,铺层方式对产品的性能有很大的影响,李仁年和刘有亮[3]通过对风力机叶片进行铺层设计,分析出增加叶片梁帽位置的铺层层数对风机的固有频率比其他位置的影响大。JIANG等[4]对T700/2510织物和单向复合正弦波板在轴向准静态冲击下的破坏模式和能量吸收特性进行了数值研究,分析纤维角度的变化对复合正弦板压溃性能的影响。段端祥和赵晓昱[5]利用有限元软件Optistruct对碳纤维复合材料电池箱铺层顺序进行优化,得到最佳的铺层分布方案,轻量化效果明显。目前国内外主要通过采用复合材料对汽车零部件进行轻量化设计,关于复合材料铺层方式对电池箱盖稳定性能的影响研究较少。
本文作者利用有限元分析软件对电池箱盖进行铺层比例、铺层顺序和铺层厚度设计,并通过对纤维增强材料铺层方案分析,探究铺层参数对电池箱盖模态及稳定性能的影响。
1 复合材料电池箱盖铺层设计
1.1 铺层设计原理分析
复合材料的铺层设计实际上就是层合板设计,由单层的特性来确定层合板中各纤维层的铺设角度、铺设层数以及铺层顺序。由于纤维和基体材料性质差异很大,在单层复合材料层中沿纤维方向的性能和垂直纤维方向的性能变化很大,形成了正交各向异性性能[6]。
层合板设计任务是根据单向板的性能确定层合板中铺层的铺设方向、各铺层的铺层比例、各定向铺层的顺序等。对于层合板性能而言,不仅与各铺层的材料性能有关,而且还与各铺层的材料取向、铺设比例以及各层的堆叠顺序有关。因此,通过改变各铺层的材料主方向及叠放顺序设计出所需力学性能的层合板,而不需要改变铺层的材料情况[7-8]。
1.2 铺层方案设计
本文作者研究的纤维增强材料电池箱盖是采用某玻璃纤维/环氧预浸料材料层叠固化而成,将电池箱盖的三维模型导入ANSYS中进行网格划分和铺层方案设计,有限元模型如图1所示,纤维每层厚度为0.3 mm,材料性能如表1所示。

图1 电池箱盖有限元模型

表1 研究中使用的玻璃纤维的材料力学参数
对于复合材料纤维铺层设计而言,铺层方案存在多种可能性,通过简化,设计中采用0°、45°、-45°三个方向进行铺层,通过设计不同铺层比例(A1、A2、A3)及不同铺层角度(A2、B1、B2)和铺层厚度(B1、C1、C2)几种方案来探究铺层比例、铺层角度和铺层厚度对复合材料电池箱盖模态及力学性能的影响,其中铺层方案表示方法为[0m/(±45)n]s(m、n≠0,m表示 0°连续层数,n表示±45°层铺层数,s表示对称铺层)。

表2 电池箱盖铺层方案
2 模态分析
2.1 模态分析有限元理论
通过有限元法[9-11]对系统结构划分网格,将无限自由度的系统转化成多自由度的系统,得到多自由度的运动微分方程:
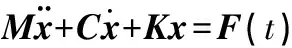
(1)
式中:M为系统质量矩阵;C为系统阻尼矩阵;K为系统刚度矩阵;F(t)为结构的激振力向量。
文中电池箱盖采用静态模态分析,无外力作用,即F(t)=0;并且在求解结构自由振动的固有频率和振型时,一般阻尼对它的影响不大,可忽略阻尼对系统的影响,得到无阻尼自由振动方程:
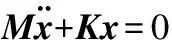
(2)
对应的结构自振频率方程:
(3)
式中:ωn为结构固有频率。
对于复合材料电池箱盖是各向异性体,单元刚度矩阵为各向异性单元,单元刚度矩阵:
(4)
式中:D为弹性矩阵;Bi、Bj分别为应力、应变关系矩阵。
(5)
式中:m为单元内铺层数;Dj为第j个铺层的弹性矩阵;tj为第j个铺层的厚度;h为单元厚度。
对于复合材料电池箱盖来说,电池箱盖铺层层数、铺层顺序、铺层方向角均影响电池箱盖的刚度矩阵K;壳铺层厚度改变会影响壳结构的质量矩阵。这些铺层因素的改变最终影响电池箱盖结构频率发生变化。
2.2 铺层方式对模态的影响
在有限元软件ANSYS Workbench中,对所建有限元模型进行约束模态分析。选取电池箱盖法兰边作为固定约束位置,选取计算电池箱盖约束模态的阶数为5阶,分析不同铺层方式下的模态值。表3是不同铺层方案下的1~5阶模态固有频率。
(1)A1、A2、A3三种铺层方案是铺层顺序和总层数相同,±45°的纤维铺层比例依次增加,从表3中可看出;电池箱盖的模态固有频率关系是A3>A2>A1,表明随着±45°纤维层比例的增加,电池箱盖的固有频率不断增加。(2)A2、B1、B2三种铺层方案采用不同的铺层顺序,总层数和铺层比例相同,电池箱盖的一阶固有频率关系为B1>B2>A2,其中B1、B2采用对称铺层的方式,可看出采用对称铺层的一阶固有频率高于非对称铺层;比较方案B1和B2的模态值,B1的固有频率高于B2的固有频率,表明0°铺层纤维在外侧时的固有频率强于±45°纤维在最外层时的固有频率。(3)铺层方案C1、B1、C2铺层厚度不同,厚度关系为C1>B1>C2,从表3可看出电池箱盖的固有频率关系为C1>B1>C2,可以得出随着铺层厚度的增加,电池箱盖的固有频率不断增加。
另外,根据计算结果,尽管采用不同的铺层方案,但具有相同的振型;电池箱盖的一阶振型为中部局部振动,二阶振型为前后振动,三阶振型为前、中、后三部分振动,四阶振型为左右振动,五阶振型为壳大面积振动。铺层方案B1前五阶约束模态振型如图2所示。

图2 铺层方式B1振型分布
3 稳定性分析
新能源汽车在行驶过程中,电池箱会受到横、纵、垂向3个方向的振动,分别用X、Y、Z向来表示,其中沿Z向的振动最大。本文作者根据GB/T 31467.3-2015中X、Y、Z方向的振动频率与功率谱密度,通过有限元分析软件模拟电池箱盖在运动过程中的随机振动,探究不同铺层方式下的最大应力及最大变形量,X、Y、Z三个方向随机振动PSD如图3所示[12-14]。

图3 X、Y、Z方向随机振动PSD密度谱
3.1 铺层方式对应力的影响
通过固定电池箱盖的法兰边面,然后根据功率谱密度对电池箱盖施加Z向的随机振动,铺层方案如表2所示,研究不同方案下电池箱盖所受的最大应力,图4是不同铺层方式下电池箱盖所受的最大应力。
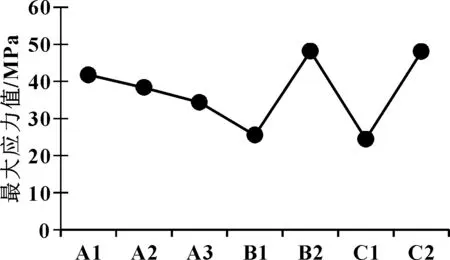
图4 不同铺层方式下的最大应力
从图4可看出:±45°纤维由40%增加到60%时,电池箱盖受到的最大应力降低了9.2%,当纤维比例从60%增加到80%时,其最大应力降低了10.5%,表明随着±45°体积分数的增加,电池箱盖的强度不断增加;通过对比不同铺层顺序方案A2、B1、B2,其最大应力关系为B1 图5 不同铺层方式下的应力云图 图6是不同铺层方式对电池箱盖的最大变形量的影响。 图6 不同铺层方式下的最大变形量 从图6可看出:纤维铺层比例对电池箱盖的最大变形量的影响与电池箱盖受到的最大应力值类似,铺层方案A1、A2、A3最大变形关系是A3 基于复合材料铺层基本原理,采用ANSYS软件对不同铺层方案下壳的模态及力学性能进行分析,对比不同铺层下的固有模态、最大应力值及最大变形量,并绘制不同铺层方案下的应力云图,得出了不同铺层方式对电池箱盖性能的影响规律。 (1)采用不同的铺层方案可以改变电池箱盖的固有频率,选择合适的铺层方案可以有效避免共振现象的发生。 (2)随着±45°铺层比例的增加,电池箱盖的模态和稳定性不断增强;铺层顺序对电池箱盖模态量影响效果不显著,但对最大应力值有明显的影响,当0°纤维在最外侧时比±45°纤维在最外侧时应力值降低47%。 (3)采用对称铺层有利于提高电池箱盖的固有频率,电池箱盖外层纤维铺层方式对箱盖的应力值影响较大,随着铺层厚度的增加,电池箱盖的稳定性能不断提升。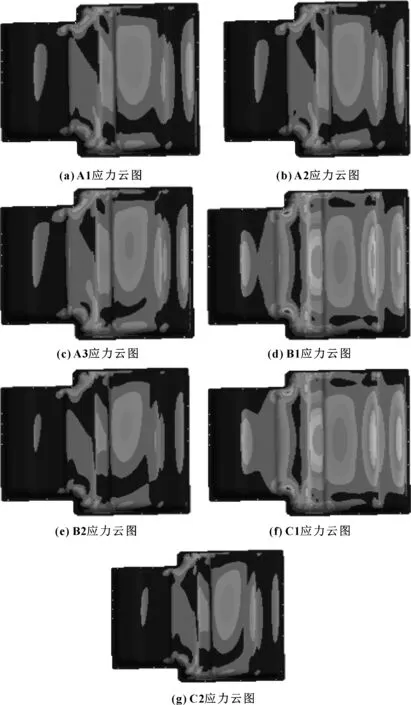
3.2 铺层方式对变形量的影响

4 结论

