关于距离问题的几点思考

南京师范大学附属中学江宁分校(211102) 姜 红

1 问题呈现

近日笔者在教学中遇到这样的一个问题:在正方形ABCD中,边长AD=6,连接AC、BD,P是正方形边或对角线上一点,若PD=2AP,求AP的长.

分析因为点P的位置可能在边或者对角线上,画出图形后要分三种情况:P在AD上,P在AB上,P在AC上.另外三条线段上不存在满足条件的的点.

解答:当点P在AD上时(如图1),因为PD=2AP,所以当P在AB上 时(如 图2),设AP2=x,则DP2=2x,在RtΔADP2中,x2+62=(2x)2,解得(负值舍去).当P在AC上时(如图3),作P3Q⊥AD于点Q,设AQ=x,则P3Q=x,因为PD=2AP,所以RtΔDP3Q中,又因为AD=6,所以解得所以

综上所述:

图1

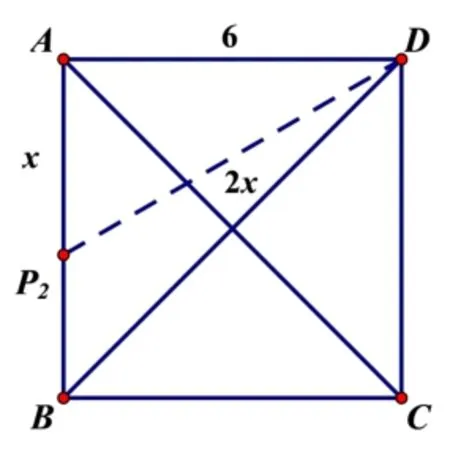
图2

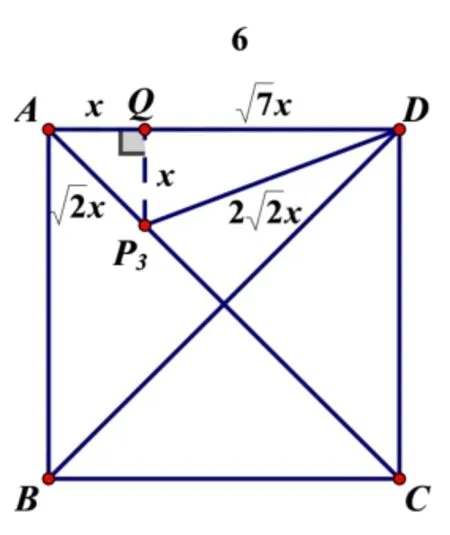
图3

2 问题提炼

以上问题,因问题背景中正方形的特殊性,解题时可利用等腰直角三角形,设元建立方程求解.但是,到两定点距离之比为1:2 的点的轨迹到底是什么呢?这个问题在中学数学中没有特别研究过.平面几何中,只研究过:到两定点A、B距离相等(即距离之比为1:1)的点的轨迹,它是线段的中垂线.至于比值是1:2 的时候到底如何,不妨用工具先实验一下.

3 实践操作

几何画板绘制图形后追踪得——点P的轨迹是圆(如图4).此圆与直线AB的交点C把线段AB内分为1:2,点D把线段AB外分为1:2.

据此实验可猜想:此圆圆心的位置在线段BA延长线上点O处,且而OP是定长.(如图5).以下来证明上面的猜想.

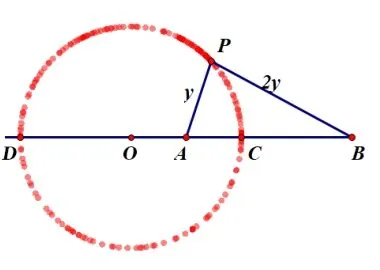
图4

图5

4 用平面几何证圆

证法1 确定圆心与半径

在BA延长线上取点O使得连接OP(如图6).以下来证明OP的长为定长不妨设AP=y,AB=3x,则BP=2y,OA=x,在△PAB中,相当于知道三边长,求高.作PH ⊥AB于点H,设AH=m,则BH=3x－m,由PH2=PA2－AH2=PB2－BH2得:y2－m2=(2y)2－(3x－m)2,解得:可得所以

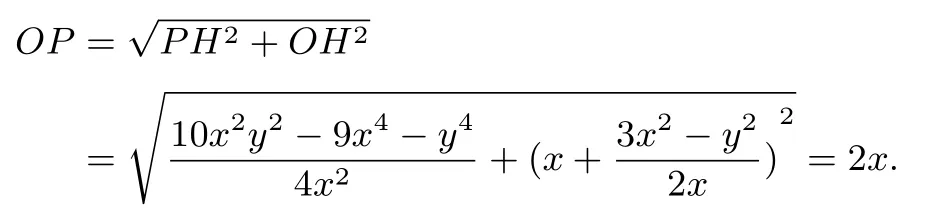
即:点P到定点O的距离为定长2x.故点P的轨迹是以O为圆心,2x为半径的圆.

证法2 确定圆的直径

联想三角形角平分线的性质——角平分线分对边所成线段之比等于夹这角两边之比,作∠APB的平分线和外角∠APE的平分线.则点C把线段AB内分为1:2,点D把线段AB外分为1:2,且PD ⊥PE.因为点C、D均为定点,故CD为定长.故点P的运动轨迹是以CD为直径的圆.

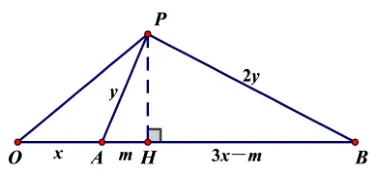
图6

图7

5 用解析几何求圆

证法3 确定满足条件的点的轨迹方程

以直线AB为x轴、AB的垂直平分线为y轴建立平面直角坐标系(如图8).

设P(x,y),AB=2a,则B(a,0)、A(－a,0).因为PB=2PA,所以

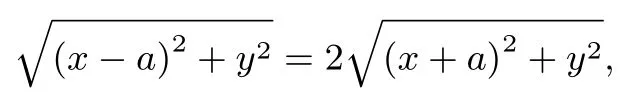
所以

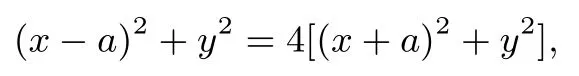
整理得:

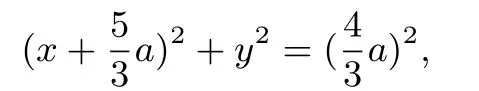
可知点P的轨迹是以为圆心,以为半径的圆.

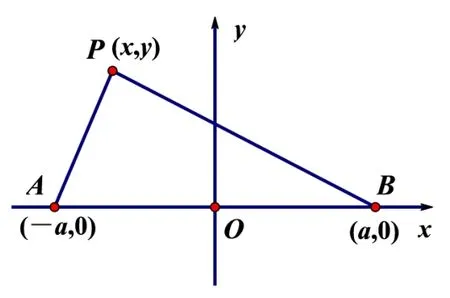
图8

6 问题一般化

以上论证可以推广到到两定点距离之比为定值1:k(k /=1)的时候:

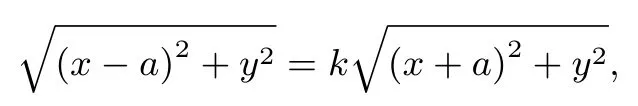
所以

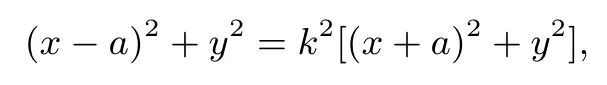
整理得:

可知点P的轨迹是以为圆心,以为半径的圆.

此圆是一个以1:k的定比内分和外分定线段AB的两个分点的连线为直径的圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿波罗尼斯圆,也叫阿氏圆.用刚才的证法2,一样可以论证出此点的轨迹是圆.当k=1 时,该点的轨迹是线段AB的中垂线.

7 问题联想

到两条相交直线距离相等的点的轨迹是四个交角平分线所在的直线(如图9).到两条平行直线距离相等的点的轨迹是与两直线平行的一条直线(如图10).到两条相交直线距离之比为定值的点的轨迹是什么呢(如图11)?

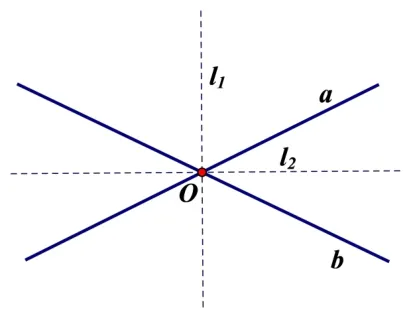
图9

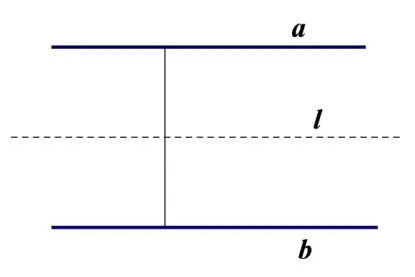
图10

不妨如此思考,到直线a距离为某定值(如PA)的点的轨迹是两条平行线l1、l2,到直线b距离为kPA的点的轨迹是另两条平行线l3、l4,所求的点是这四条直线的交点,共四种情况.

现选取四个交点之一的点P来分析,考虑图中l1//a、l3//b、PA⊥a、PB⊥b,可得△PAC～△PBD,故PC:PD=PA:PB=1:k.(如图12)

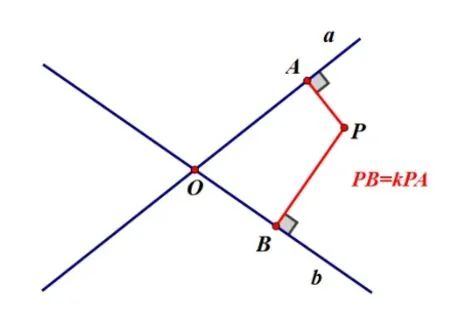
图11

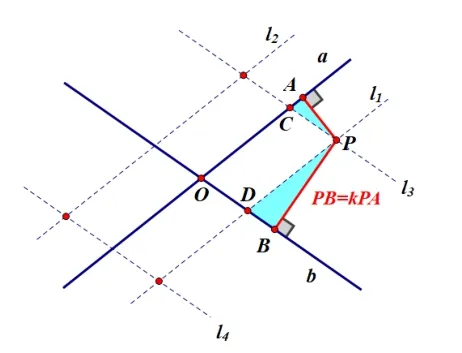
图12

事实上,两条相交直线构成平面斜坐标系,交点是原点,两直线分别是x轴、y轴.这样,原问题等价于到两坐标轴距离之比为定值的点的轨迹.即:P(x,y),其中|y|=k|x|.可知这样的点的轨迹是两条过原点且斜率绝对值为k的直线y=kx和y=－kx(如图13).

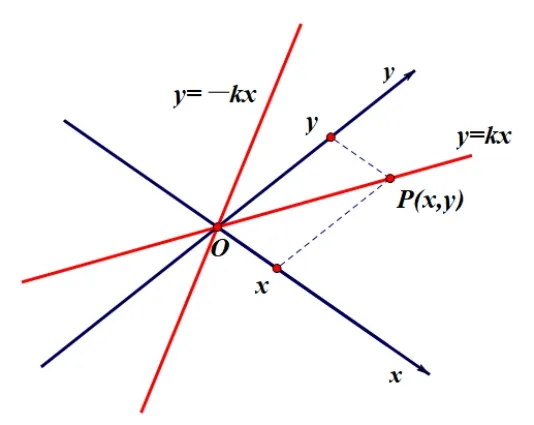
图13