“互联网+”背景下影响网络评教因素的实证研究

郭啸 朱锦松 徐寒

摘要：随着“互联网+”战略上升至国家战略，“互联网+教育”更加成为高等教育研究领域的热点。在高等学校教学质量管理模块中，授课质量是反映教师教学状况的重要指标，学生通过网络对进行评教已经成为教学质量管理中不可或缺的组成部分。通过对网络评教数据分析，对非教学的因素相关性进行观测，考察不同因素是否对评教分产生影响，得出评教分数与教师的教学能力以及非教学因素的隐含关系与价值；通过对网络评教数据的挖掘，为提高网络评教分数的科学性提供支撑。

关键词： 互联网+；网络评教；相关性分析；回归分析；实证研究

★基金项目：本文系江苏省教育科学规划重点资助课题（编号：B-a/2015/01/033）；南京邮电大学教学改革研究项目（编号：JG04016JX99）；南京邮电大学项目“非双一流教学基本状态数据库系统的构建——以南京邮电大学为例”（编号：GJS-XKT15012）的部分成果。

引言

随着2015年7月4日国务院总理李克强签发了《关于积极推进“互联网+”行动的指导意见》，大大推动了“互联网+教育”的模式的发展。在高等教育教学质量管理的模块中，通过网络与评教相结合的网络评教，已是当下的主流，且在高校教学质量管理中被得到广泛运用。网络评教对于提高高校教师的教学质量起到了较大的促进作用，已成为评价课程教学质量和教师教学水平的重要手段之一。如何利用学生的网络评教分数判定教学质量，已经引起了广大教育教学工作者的关注。

1、研究方法

研究采用SPSS20.0，将评教数据进行分析和挖掘，探究网络评教分数与非教学因素，如选课人数、课程类型、学生年级之间的相关性，因此，将采用如下的分析方案步骤：首先是数据分析，通过均值和标准差比较，考察不同因素是否对评教分数产生影响；其次采用相关性分析对非教学因素的相关性进行分析，得出非教学因素影响评教分数中的方式；最后通过数据挖掘，通过对课程利用线性回归进行预测以及采用快速聚类算法，将特征相似的课程进行聚类，根据类型设立不同的评教指标从而提高网络评教分数的科学性。

2、数据准备

数据库中只有评教明细数据，但在SPSS进行数据分析时，需要知道每一门课程的总评教分和选修该门课程的总人数，开课年级、课程类别等，所以需要对原始数据进行处理，得到具有如下数据结构的“按课程汇总评教分数表”，包含“授课班号”“教师编号”“教师姓名”“学期”“课程类型”“年级分类”“评教分数”“人数”“人数分类”等字段。此外，其统计分类必须是值类型，因此将数据表“按课程汇总评教分数表”导入SPSS后，需要对部分列进行数值化处理：将课程类型列定义值标签为：1=“理科课”，2=“文科课”，3=“思想政治課”，4=“外语课”，5=“实验课”，6=“体育课”。将年级分类列定义值标签为：1=“低年级”，2=“高年级”；其中低年级代表的是一年级和二年级的课程，高年级代表的是三年级和四年级的课程。将选课人数分类列定义值标签为：1=“小于60人”，2=“60-100人”，3=“100-150人”，4=“150-200人”，5=“大于200人”。

3、实证研究

3.1 均值和标准差比较

将评教成绩分别按课程类型、按选课人数和按年级分组进行评教分数和标准差比较。数据显示评教分数与课程类别相关，外语课、思想政治课和体育课的评教分数明显高于总体平均分，理科课和文科课的评教分数明显低于总体平均分；小班授课与大班授课评教分值差异大，其中小于100人的课程的评教分均值相近，且均高于平均分，而超过100人的评教分均值相近，且均低于平均分，表明大班授课的教学效果弱于小班授课；此外，评教分数与年级高低相关，低年级的评教分数高于总体平均分，高年级的评教分数低于总体平均分。标准差方面，文科课和理科课的标准差在所有课程中最大，高年级的标准差高于低年级，选课人数小于60人课程和100-150人课程的标准差最大，标准差越大表明评分结果分布越离散。具体情况参见表1至表3。

3.2 相关性分析

相关性分析是指对两个或多个处于同等地位的随机变量间的相关关系的统计方法，从而衡量变量因素的相关密切程度。若这些变量都是连续性的变量，则需要使用Pearson相关性分析。研究通过Pearson分析，对年级分组、课程分组和选课人数分组为因素与评教分数做相关分析，观察这三个因素对评教分数的具体影响。数据显示评教分与选课人数、课程类别、年级关系的线性相关关系依次增强。此外，从相关矩阵数据还可以看出：sig=0.00，说明评教分数与选课人数、课程类别、年级的高低的关系呈现出明显的线性相关关系。具体情况参见图1。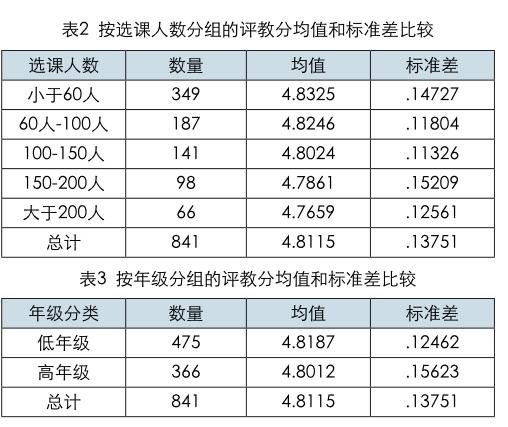

3.3 回归分析

通过相关性分析发现评教分数除了与教师的教学水平相关以外，还与课程类别、选课人数、年级分类等因素相关。但因素之间具体是如何影响评教分数，需要使用回归分析。回归分析是指确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。因此，以年级分组、课程分类、选课人数分类为因素与评教分数做回归分析，得出三者与评教分的回归方程，为评教分=4.668+0.011*课程类型（-0.074）*年级分类+（-0.009）*选课人数。即数据显示对评教分数影响最为显著的是课程类型，具体情况参见图2。