基于静动载试验的桥梁承载能力评估研究

傅 莉

（山西省交通建设工程质量检测中心（有限公司），山西 太原 030006）

0 引言

桥梁在交通线路中占有重要地位，是交通线路的大动脉，随着结构使用寿命增长，大多数公路在役桥梁在多种因素的耦合作用下会出现不同程度的损伤，导致桥梁承载能力和耐久性等性能出现不同程度的降低[1]。根据交通运输部发布的《2018年交通运输行业发展统计公报》[2]中数据显示（2019年的数据未公布），截止2018年年底我国公路总里程达到484.65万km，相比上年增加7.31万km，我国在役的公路桥梁85.15万座、5 568.59万m，相比上年增加1.90万座、342.97万m，其中特大桥梁5 053座、902.69万m，大桥98 869座、2 637.04万m。《2016—2022年中国桥梁管理与养护产业现状调查及十三五发展定位分析报告》中指出，目前我国公路路网中在役桥梁技术等级为三、四类的带病桥梁高达30%，超过10万座桥梁为危桥。十二五期间，我国改造危桥1.7万座/151万延米。此外，我国在役桥梁老龄化非常严重，对比中美30年桥龄的桥梁占比可以总结出，美国桥梁老龄化从18%增长到60%，用了约60年的时间，而中国却不到30年，因此，在经济高速发展期间，我国建成的桥梁具有的特点有：桥梁总量大、使用周期短、安全隐患多，大多数桥梁存在未老先衰，桥梁老龄化的问题比较严重。

如今国内外经常使用的在役桥梁承载力评估的方法有：基于桥梁设计规范的评估方法、桥梁外观调查的方法、静动载荷载试验实测法、专家系统评估方法和基于概率理论的可靠度评估方法[3]。合肥工业大学任伟新[4-5]团队基于美国1876年建成的某桥设计资料建立了初始有限元模型并进行了模态和振型分析，通过外部环境激励试验和模态参数识别方法得到了该桥的模态参数。通过该桥实测结果对初始有限元模型进行修正，应用修正后的有限元模型进行荷载组合加载分析，并对该桥结构实际承载力进行了评估和分析。刘洋[6]以某斜拉桥为研究背景，采用响应面方法并增加有模型和无模型预警，全面地进行了根据实时监测数据的桥梁结构有限元模型修正，并评估了该桥的承载能力，提出了新的方法。长沙理工大学张建仁[7]团队基于在役公路桥往往存在超载的现象，对一座在役多年的钢筋混凝土梁桥进行了实地的承载能力破坏性试验。把千斤顶当作超载情况下的重车荷载，分析了实桥从开始加载至结构完全破坏整个过程的力学行为，特别是在承载能力达到极限状态下的力学性能。垄江烈[8]等基于分析并比较了桥梁在竣工状态下的结构基频与服役若干年后的结构基频变化，提出了一种新的原始指纹评定方法。张文献[9]等通过实验室模型试验，提出了桥梁的裂缝高度、宽度等多种因素与其结构承载能力的快速评定公式。Hover[10]对某钢筋混凝土简支梁做了动力特性方面的试验，通过实测结构的基频推导出该结构的动刚度，因此，提出了桥梁承载力与动刚度的回归公式，并推广应用于桥梁结构承载力评估。

综上所述，许多文献对桥梁承载能力的评估进行了较多的研究，由于在役的公路桥梁受当时的设计理论、较低的荷载标准、技术和管理水平等限制，结构承载能力的标准较低，不能适应日益增长的交通量和超载交通，急需对服役多年的桥梁给出合理并科学的评估方法，因此，本文根据以某准跨径为13 m、横向25片空心板、桥面宽40.1 m的三跨简支板桥为背景桥的静动载试验来分析和定量研究桥梁的承载能力，为其他桥梁承载能力的评估提供指导。

1 桥梁承载能力评定方法

1.1 加载效率

依据《城市桥梁检测与评定技术规范》（CJJT 233—2015）中的规定，静力试验荷载的效率系数ηq宜介于0.95～1.05之间。就某一加载试验项目而言，试验荷载加载效率按式（1）所确定的原则等效换算而得：

式中：ηq为静载试验荷载加载效率；Ss为位移或内力的最大计算效应值；S为位移或内力的最不利效应计算值；（1+μ）为按规范计算的冲击系数。

1.2 校验系数

桥梁结构的校验系数按式（2）计算：

式中：Se为实测弹性变位或应变值；Ss为理论计算变位或应变值。

静力荷载试验结构校验系数ξ是一个重要的评定指标。当静载试验结构校验系数小于1时，表明试验桥梁的实际承载状况强于理论的状况。

1.3 相对残余应变

总变位（或总应变）：

弹性变位（或弹性应变）：

残余变位（或残余应变）：

相对残余变位或应变：

式中：Si为加载前的测试值；SI为加载达到稳定时测试值；Su为卸载后达到稳定时测试值。

2 静动载试验研究

2.1 静载试验分析

2.1.1 试验挠度数据分析

2.1.1.1 跨中截面最大正弯矩对称加载

在各级试验荷载作用下，实测某桥1号孔跨中截面各测试截面测点的挠度校验系数为0.16～0.54之间，表明能够满足《公路桥梁承载能力检测评定规程》（JTG/T J21—2011）《公路桥梁荷载试验规程》（JTG/T J21-01—2015）（以下简称“试验规程”）及《城市桥梁检测与评定技术规范》（CJJT 233—2015）（以下简称“评定技术规范”）中满足“评定规程”、“试验规程”及“评定技术规范”中小于1.0的要求。

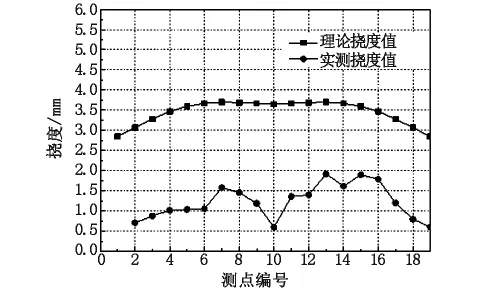
图1 工况1跨中截面挠度理论值与实测值对比

挠度沿桥面宽度的分布情况如图1所示，由图1可见挠度及横向分布与理论值相比基本一致，通过跨中截面最大正弯矩对称加载时，分析测点跨中截面的挠度，表明桥梁结构横向刚度良好且传力正常，其中理论计算最大挠度3.7 mm，实测最大挠度2 mm。

2.1.1.2 跨中截面最大正弯矩偏心加载

试验荷载作用下，背景桥跨中截面各空心板的各测试截面测点的挠度校验系数为0.16～0.54之间，满足“评定规程”、“试验规程”及“评定技术规范”中小于1.0的要求。

图2 工况2跨中截面挠度理论值与实测值比较

根据挠度沿桥面宽度的分布情况如图2所示，由图2可见挠度及横向分布与理论值相比基本一致，通过跨中截面最大正弯矩偏心加载时，分析跨中截面的挠度，表明桥梁结构的横向刚度良好且传力较好。

2.1.2 试验应变数据分析

2.1.2.1 对称加载

在试验对称荷载作用下，背景桥1号孔跨中截面各空心板的测试截面测点的应变校验系数为0.14～0.40 之间，满足“评定规程”、“试验规程”及“评定技术规范”中小于1.0的要求，由此说明试验荷载作用下该截面桥梁的实际受力状况要优于理论受力状况。

应变沿横桥向的分布情况如图3所示，由图3可见应变及横向分布与理论值相比变化趋势基本一致，通过对称加载时分析应变数据，表明结构横向刚度良好且传力较好。

图3 工况1跨中截面测点应变理论值与实测值对比

2.1.2.2 偏心加载

试验偏心荷载作用下，背景桥1号孔跨中截面各测试截面典型测点的应变校验系数为0.16～0.33之间，满足小于1.0的要求，由此说明试验荷载作用下该截面桥梁的实际受力状况要优于理论受力状况。

图4 工况2跨中截面测点应变理论与实测值对比

应变沿横桥向的分布情况如图4所示，由图4可见应变及横向分布与理论值相比基本吻合，通过偏心加载时分析应变数据，表明桥梁结构的横向刚度较好且传力较正常。

2.2 动载试验分析

对背景桥进行有限元分析，离散处理，采用Midas civil空间有限元软件，有限元模型图如图5所示，运用子空间迭代法对背景桥进行模态分析，计算得到该桥的一阶自振频率如表1所示，有限元计算的振型图如图6所示，计算和实测振型结果对比如表2所示，本次动载试验应用脉动试验的方法测试背景桥梁结构的自振频率，频谱分析见图7所示。

图5 背景桥的有限元模型图

表1 实测频率和有限元计算频率对比表

图6 背景桥一阶振型图

表2 计算振型和实测振型结果对比

图7 竖向频谱分析图

经过分析计算及实测分析，由表1可知，该桥自振频率实测值为10 Hz，有限元软件计算频率约为9.1 Hz，误差9%，表明两者之间误差较小且桥梁结构实际刚度大于计算刚度，满足工程上精度的要求，本次试验桥梁的计算振型与实测振型形状相似程度很高，说明了计算模型的正确性，而且一阶竖向振型的阻尼比4.58%，属于低阻尼振动，符合工程振动的情况，且其阻尼比与国内其他类似结构的阻尼比接近。

3 结语

a）通过计算分析，背景桥实测的挠度和应变校验系数分别在0.14～0.40和0.16～0.54之间，结构刚度和强度满足工程上的要求。

b）从试验结果分析，实测挠度的横向分布规律与理论挠度的横向分布规律比较吻合，表明桥梁结构的横向刚度较好且传力正常。

c）本次试验桥梁的计算振型与实测振型形状相似程度很高，说明了计算模型的正确性，一阶竖向振型的阻尼比4.58%，属于低阻尼振动，其阻尼比与国内其他类似结构的阻尼比接近。

d）实测振型与理论值吻合，自振频率实测值为10 Hz，而有限元软件计算频率为9.1 Hz，其两者的误差为9%，两者比值为1.1，说明两者之间的误差能满足工程的需求，同时说明结构实际刚度较大。