新型波形钢腹板组合箱梁挠度特性

秦翱翱，刘世忠，毛亚娜，蔡明昊，王文哲

(兰州交通大学 土木工程学院，兰州 730070)

近年来，波形钢腹板组合箱梁凭借自身独特的结构形式和优越的力学性能受到国内外学者广泛关注，该类箱梁自重较轻，施工方便，由于波腹板的手风琴效应，使得箱梁顶板和底板在纵桥向的变形不受约束，预应力效率被极大地提高，避免了腹板混凝土的开裂问题[1-2].与传统混凝土箱梁相比，波形钢腹板较薄且自身褶皱效应明显，抗剪刚度较小[3-5]，因此计算波形钢腹板组合箱梁的挠度须考虑这种影响.文献[6]从剪力滞的本质出发，引入纵向位移函数研究波形钢腹板PC箱梁挠度，并基于有限元和室内试验验证了计算结果.文献[7]推导了波形钢腹板组合箱梁在考虑剪切变形影响的挠曲线初参数方程，结合模型试验和空间有限元，对比分析了三种典型荷载作用下的挠度特性.文献[8]推导了波形钢腹板组合箱梁剪切附加挠度的控制微分方程，并进行了剪切变形的影响规律参数分析.文献[9]基于初等梁理论提出了波形钢腹板组合箱梁考虑剪切变形的挠度计算方法，结合模型试验和有限元模型，给出了考虑剪切变形影响的剪跨比界限值.

以上既有研究均针对混凝土顶板、波形钢腹板、混凝土底板组成的波形钢腹板组合箱梁.而对于混凝土顶板、波形钢腹板、钢底板组成的新型波形钢腹板组合箱梁，则研究不多，以钢底板代替混凝土底板，除保持波形钢腹板组合箱梁优势外，还充分发挥混凝土抗压和钢材抗拉的性能，避免了混凝土底板因收缩徐变及跨中正弯矩产生的开裂问题，有效地提高了结构的抗裂强度、刚度和耐久性[10].

考虑混凝土和钢材的材料特性，在已有研究的基础上，假设无界面滑移的影响，运用能量变分原理，提出了一种忽略界面滑移、考虑剪力滞、剪切变形双重影响的挠度计算方法，结合模型梁试验和空间有限元，分析理论值、有限元值与实测值的误差，研究初等梁理论挠度、剪力滞挠度和剪切变形挠度占总挠度的比例，以供工程设计参考.

1 剪力滞翘曲位移模式

箱梁发生弯曲变形时，由于剪力滞效应的影响，横截面上任意一点的纵向位移由两部分产生，即弯曲纵向位移和翘曲纵向位移，而根据Timoshenko梁变形理论[11]，箱梁发生弯曲变形时，梁截面产生剪切变形如图1所示，梁截面上任意一点的纵向位移函数表达式如下[12]：

u(x,y,z)=-zφ(x)+f(y)U(x),

(1)

图1 Timoshenko梁变形Fig.1 Deformation of Timoshenko beam

其中：

(2)

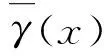
波形钢腹板由于自身的形状特性，其有效剪切模量Ge与平钢板的剪切模量Gs存在如下关系[13]：

(3)

其中：

式中：Es为钢板的弹性模量;v为钢板的泊松比;a、b、α分别表示波形钢腹板尺寸,如图2所示.

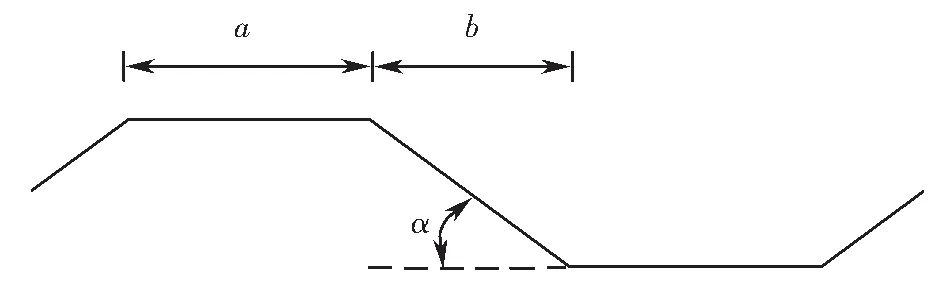
图2 波形钢腹板尺寸Fig.2 Dimensions of corrugated steel webs

当考虑箱梁的剪力滞效应时，需选取合适的剪力滞翘曲位移函数来描述截面剪切变形不均匀现象.文献[14]选取经典的二次抛物线作为研究对象，其表达式如下：

f(y)=

(4)

附加轴向位移：

(5)

式中：A1为顶板面积;A2为悬臂板面积;A3为底板面积;A为横截面总面积,其余各参数如图3所示.

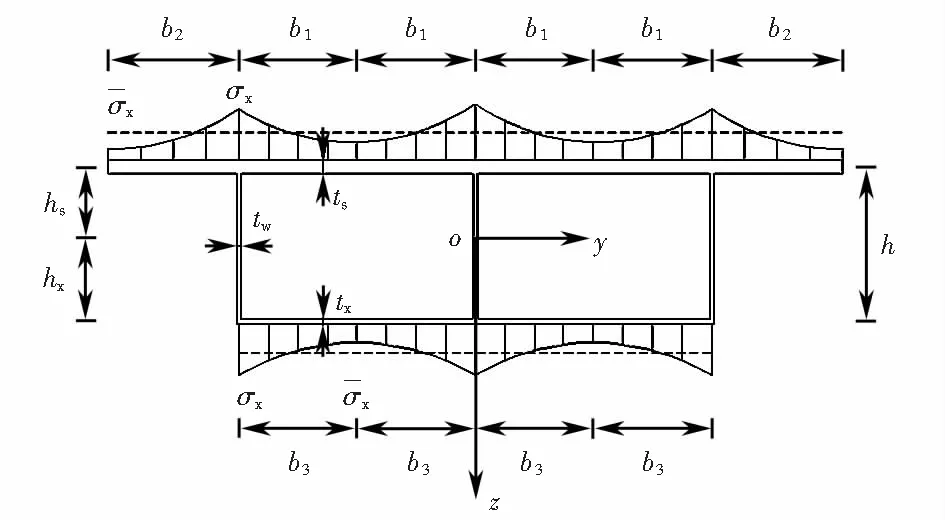
图3 箱梁剪力滞效应Fig.3 Shear lag effect of box girder

2 基本变分方程的推导

箱梁外力势能：

(6)

箱梁的顶板、悬臂板及底板应变能：

(7)

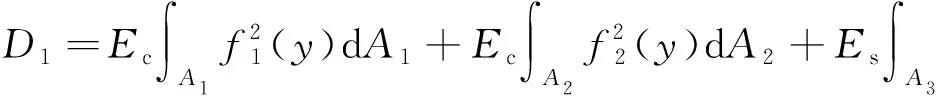
式中：D2为双室箱梁的抗弯刚度.

波形钢腹板剪切应变能：

(8)

由最小势能原理可知，双室箱梁体系的总势能一阶变分为零[15]，即：

(9)

其控制微分方程和边界条件如下：

(10)

剪力滞微分方程：

U″-k2U=μQ(x).

(11)

瑞斯纳参数[15]：

剪力滞微分方程的一般解：

U=μ(C1sinhkx+C2coshkx+U*).

(12)

式中：C1,C2均为系数,由约束条件确定;U*为剪力滞广义位移的特解.

由公式(2)、(10)可得：

(13)

对式(13)积分，可得梁的挠度理论公式：

(14)

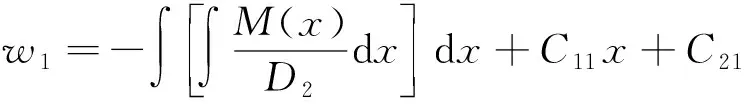
dx+C13x+C23为剪切变形产生的附加挠度.

3 简支梁的挠度计算

3.1 在集中荷载下的挠度计算

如图4所示，根据公式(12)～(14)，箱梁在跨中集中荷载作用下的挠度计算过程如下.

图4 集中荷载示意图Fig.4 Diagram of concentrated load

截面的弯矩和剪力为

(15)

由剪力滞微分方程得：

(16)

边界条件:

可得：

(17)

集中荷载作用下箱梁挠度：

(18)

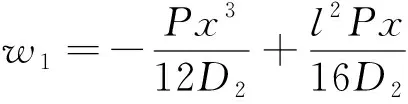
3.2 在均布荷载下的挠度计算

如图5所示，根据公式(12)～(14)，箱梁在均布荷载作用下的挠度计算过程如下.

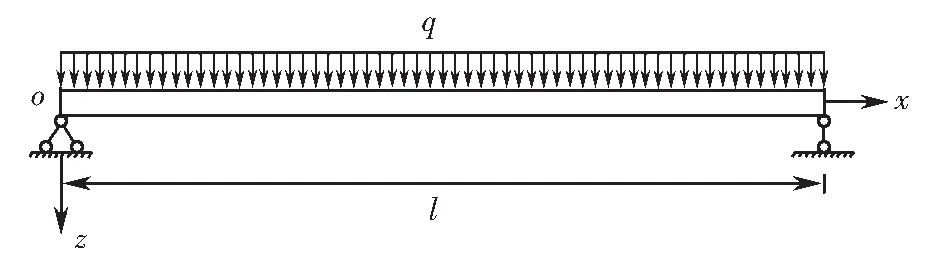
图5 均布荷载示意图Fig.5 Diagram of uniform load

截面的弯矩和剪力为

(19)

由剪力滞微分方程得：

(20)

边界条件:

U′(x=0)=0;U′(x=l)=0.

可得：

U=

(21)

均布荷载作用下箱梁挠度：

(22)

3.3 纵向加劲肋对挠度的影响

由于新型波形钢腹板组合箱梁的底板较薄，通常会在底板上设置一定数量的纵向加劲肋，在理论分析箱梁挠度时，需要考虑纵向加劲肋对挠度的影响.根据底板抗弯刚度等效原则，将加劲肋抗弯刚度平均分配到钢底板上.具体公式如下：

(23)

式中：Ii为第i个加劲肋对箱梁截面中性轴的惯性矩;Ix为钢底板对箱梁截面中性轴的惯性矩;Iu为分配后钢底板对箱梁截面中性轴的惯性矩.

4 算例

4.1 试验梁尺寸

为验证理论分析的正确性，制作了长度6 m的新型波形钢腹板试验梁，箱梁顶板为钢筋混凝土结构，混凝土强度C55，弹性模量35.5 GPa，钢筋为Ⅰ级普通钢筋，泊松比0.2；波腹板、底板、横隔板及加劲肋均由钢板焊接而成，底板和端横隔板厚度5 mm，波腹板、中横隔板及加劲肋厚度3 mm， Q345钢材，弹性模量206 GPa，泊松比0.28.其中，顶板宽1.5 m，底板宽85 cm，梁高41 cm，为单箱双室等截面，试验梁截面和波腹板尺寸如图6～7所示.

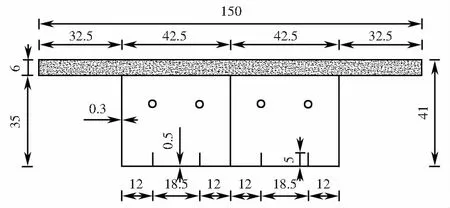
图6 试验梁截面尺寸(单位:cm)Fig.6 Section size of test beam(unit:cm)

图7 波腹板基本尺寸(单位:cm)Fig.7 Basic dimensions of corrugated web(unit:cm)

4.2 有限元模型建立

根据箱梁模型实际尺寸，运用有限元软件ANSYS建立三维有限元模型，其中，顶板采用实体单元SOLID65模拟，波形钢腹板、底板、横隔板及纵向加劲肋采用壳单元SHELL63模拟，顶板实体单元与腹板壳单元采用共节点连接，由于实体单元和壳单元具有不同的自由度，当共用节点时两者连接方式为铰接，因此须在共节点位置通过约束方程建立刚性区域[16].模型的边界条件按照简支梁设置.

4.3 试验加载方案

加载方式分为集中荷载和均布荷载，其中，集中荷载P=98 kN作用在跨中位置，均布荷载q=8.2 kN/m作用在满跨位置，加载点均在波形钢腹板与顶板相交处，以减少梁体扭转、畸变及横向弯曲带来的影响.试验梁加载如图8所示.

图8 试验梁加载示意图Fig.8 Loading diagram of test beam

5 试验结果分析

在集中荷载和均布荷载作用下，有限元模型挠度云图如图9所示，跨中左右两测点的挠度实测值、有限元值和理论计算值如表1所列.

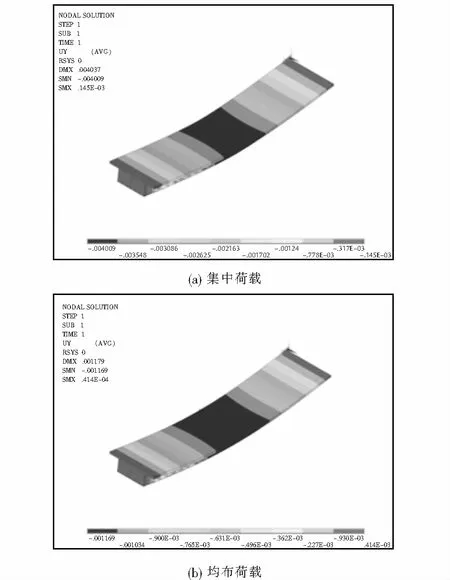
图9 有限元模型计算挠度Fig.9 Deflection calculated by finite element model

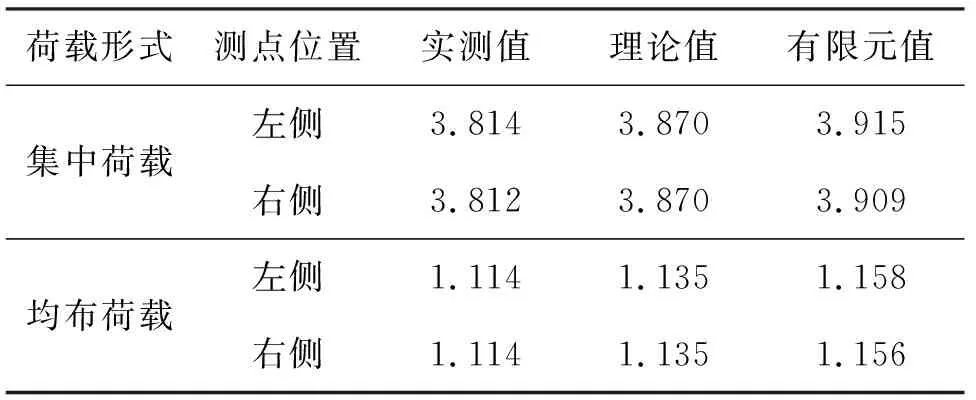
表1 不同计算方法的挠度值比较Tab.1 Comparison of deflection values of different calculation methods mm

由表1可知，与实测值相比，集中荷载作用下，理论值、有限元值的误差分别为1.49%、2.60%；均布荷载作用下，理论值、有限元值的误差分别为1.89%、3.86%，均布荷载下的理论值、有限元值与实测值误差均大于集中荷载，该计算方法对集中荷载下的挠度计算精度较高.同种荷载作用下，挠度理论值和实测值均小于有限元值，挠度有限元值偏于安全，整体实测值、有限元值和理论值误差较小，验证了理论分析方法和有限元模型的正确性.

为进一步分析初等梁理论产生的挠度、剪力滞产生的附加挠度和剪切变形产生的附加挠度占总挠度的比例大小，现定义如下：

(24)

式中：wj为初等梁理论或剪力滞或剪切变形产生的挠度;w为箱梁的总挠度;ξj为各部分挠度所占总挠度比例.

按照公式(24)之定义，给出各部分挠度值大小及所占比例，如表2所列.

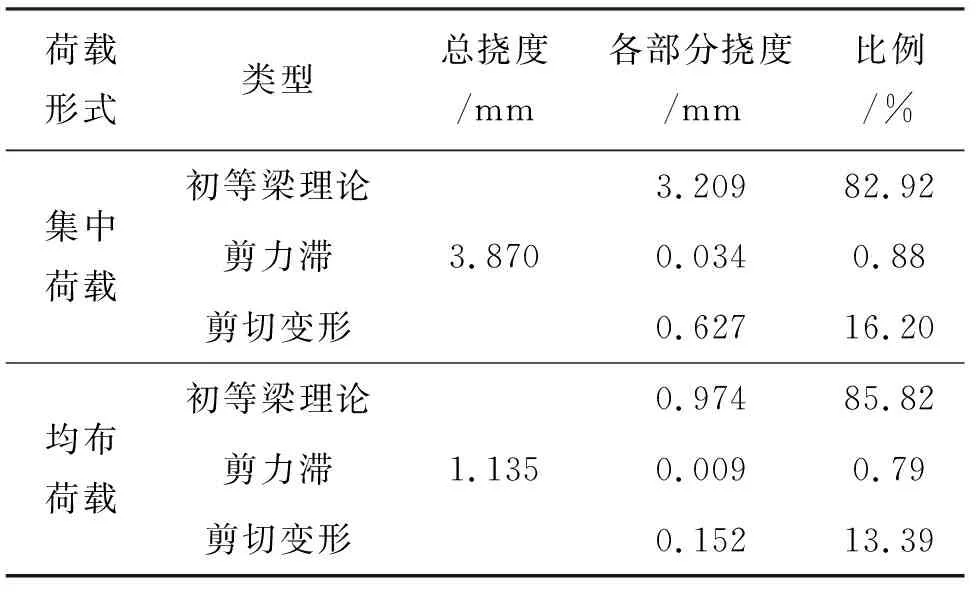
表2 不同挠度所占比例Tab.2 Proportion of different deflections

由表2可知，在计算箱梁受弯所产生的挠度时，总挠度主要由初等梁理论计算值提供，剪切变形对总挠度的贡献次之，剪力滞对总挠度的贡献最小.在两种荷载下，初等梁理论挠度占总挠度比例均大于80%，剪力滞挠度占总挠度比例均小于1%，剪切变形挠度占总挠度比例在15%左右.因此，模型梁实际挠度可按初等梁理论挠度乘以1.2倍修正系数进行计算，而对于其它不同尺寸箱梁，则需要通过进一步研究来确定系数取值.

6 影响因素分析

6.1 跨高比

为研究不同跨高比下初等梁理论挠度、剪力滞挠度和剪切变形挠度的占比规律，以模型梁为基准，保持截面尺寸不变，通过改变箱梁跨径来模拟不同跨高比.选取跨高比为10、15、20、25的箱梁，在试验荷载作用下，箱梁总挠度理论值和有限元值变化如图10所示，各部分挠度占总挠度的比例如表3所列.

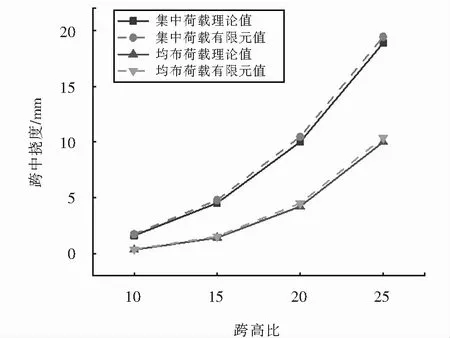
图10 不同荷载随跨高比的挠度变化Fig.10 Deflection variation of different loads with spanheight ratio

由表3可知，在集中荷载和均布荷载作用下，随着跨高比增大，初等梁理论对挠度的贡献逐渐增大，而剪力滞和剪切变形对挠度的贡献则逐渐减小；在同一跨高比下，集中荷载下的初等梁理论挠度占总挠度比例小于均布荷载，而集中荷载下的剪切变形挠度占总挠度比例则大于均布荷载，总体变化规律一致.

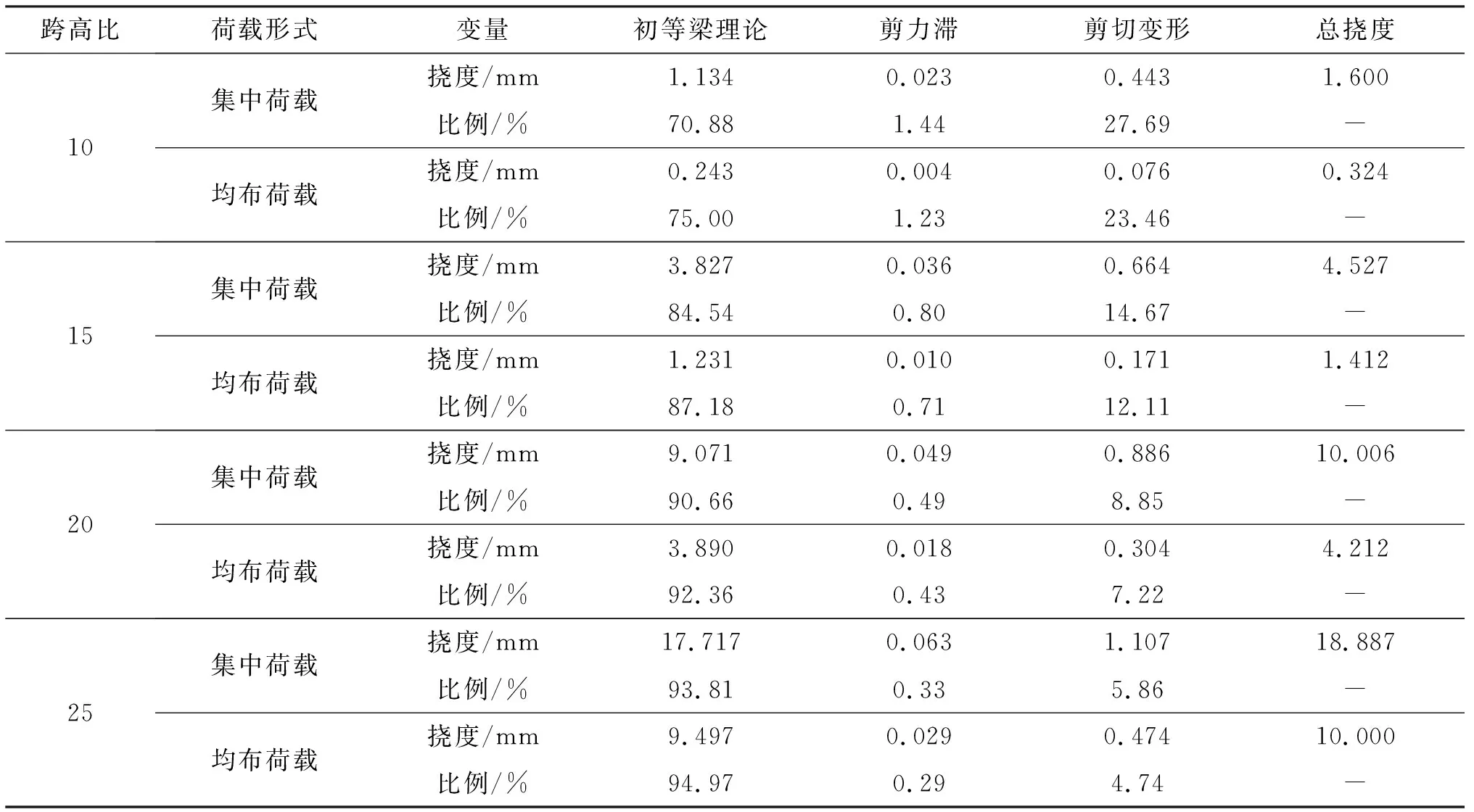
表3 各部分挠度占总挠度比例Tab.3 Proportion of each part deflection to the total deflection

当箱梁跨高比大于20时，初等梁理论挠度占总挠度比例均大于90%，剪切变形挠度占总挠度比例均小于10%，因此，当跨高比在20～25范围内，挠度修正系数可按1.08取值；当箱梁跨高比小于20时，初等梁理论挠度占总挠度比例均小于90%，剪切变形挠度占总挠度比例均大于10%，此时，挠度修正系数可按同一跨高比下总挠度与初等梁理论挠度的比值进行取值.

6.2 宽高比

为研究不同宽高比下初等梁理论挠度、剪力滞挠度和剪切变形挠度的占比规律，以模型梁为基准，控制截面宽度不变，通过改变截面高度来模拟不同宽高比.选取宽高比为2、3、4、5的箱梁，在试验荷载作用下，箱梁总挠度理论值和有限元值如图11所示，各部分挠度占总挠度的比例如表4所列.

图11 不同荷载随宽高比的挠度变化Fig.11 Deflection variation of different loads with widthheight ratio

由表4可知，在集中荷载和均布荷载作用下，随着宽高比的增大，初等梁理论对挠度的贡献逐渐增大，剪切变形对挠度的贡献逐渐减小，而剪力滞对挠度的贡献则小于1%，可忽略不计.同一宽高比下，集中荷载下的初等梁理论挠度占总挠度比例小于均布荷载，剪切变形挠度占总挠度比例则大于均布荷载，但两者相差不大.当宽高比为5时，集中荷载和均布荷载下的剪切变形挠度占总挠度比例最小，分别为12.47%和10.25%.因此，在不同宽高比下，挠度修正系数可按同一宽高比下总挠度与初等梁理论挠度的比值进行取值.

表4 各部分挠度占总挠度比例Tab.4 Proportion of each part deflection to the total deflection

7 结论

1) 与实测值相比，集中荷载下，理论值、有限元值的误差分别为1.49%、2.60%；均布荷载下，理论值、有限元值的误差分别为1.89%、3.86%.验证了本文分析方法的正确性.

2) 初等梁理论对挠度的贡献最大，剪切变形的贡献次之，剪力滞的贡献最小.

3) 剪切变形对挠度的贡献随跨高比和宽高比的增大而减小，剪切变形对挠度的贡献可通过引入修正系数来考虑.