基于灰关联理论的既有隧道衬砌背后空洞对衬砌受力的影响分析
孙寿榜,严松宏,剡永伟
(兰州交通大学 土木工程学院,兰州 730070)
随着经济的快速发展,我国已成为世界上隧道数量最多、建设速度最快的国家,施工技术已达世界领先水平[1],与此同时,部分运营隧道由于复杂的地质条件、地形条件、以及当时施工不当等原因,隧道衬砌裂缝、衬砌后空洞、二衬厚度不足等病害也越来越多[2-3].衬砌背后空洞是运营隧道中最主要病害之一,它可能导致衬砌边缘发生裂纹、开裂、失稳、跌落甚至突然坍塌[4-6].由于空洞在衬砌后面形成,所以在衬砌发生严重损伤(通常是严重开裂、剥落甚至失效)之前,很难发现空洞.常规检查空洞的方法是用锤敲击衬砌表面,然后识别空洞,然而随着科技的进步,探地雷达(GPR)为隧道衬砌质量评价提供了一种相对方便快捷的无损检测手段,探地雷达法已在隧道衬砌空洞、衬砌厚度、围岩溶洞等病害检测中得到了广泛的应用[7-10].穆伟[11]利用探地雷达对衬砌背后空洞进行了检测,对衬砌质量缺陷地质雷达波形图进行解译及分析并总结出隧道衬砌空洞缺陷的几种典型地质雷达波形特征.杨睿等[12]采用探地雷达检测衬砌背后空洞,并进行钻孔取芯验证,结果表明探地雷达用于空洞检测可行且具有较高的可信度.既有隧道存在空洞会对衬砌的轴力和弯矩产生不利影响,这也是衬砌开裂及失稳的根本原因.Yasuda等[13]给出了基于平面应变假设条件下,深埋圆形隧道衬砌背后空洞的弹性解,计算结果表明,空洞的存在使衬砌的应力状态由轴向推力变为弯矩状态,空洞的存在导致衬砌应力集中,从而导致衬砌产生不良变形和应力.Meguid等[14]通过弹塑性有限元分析,研究了不同影响因素下空洞对衬砌轴力和弯矩的影响,空洞出现在隧道仰拱处,影响较为严重,弯矩符号从负改为正,衬砌可能出现开裂.崔文艳等[15]基于隧道衬砌后空洞对结构安全影响的模型试验,通过数值分析,研究空洞在不同位置对隧道衬砌的力学行为的影响,通过对衬砌轴力和弯矩的分析,得出不同位置的空洞都会影响衬砌结构的安全性能,存在空洞的位置极易引起应力集中,衬砌破坏较为明显.
本文借助探地雷达对既有隧道进行无损检测并探明空洞的分布位置及大小,结合设计资料建立有限元数值模型,针对空洞对衬砌受力的影响进行研究.同时,引入灰色关联理论,对由于空洞而产生的衬砌附加轴力和弯矩进行灰关联分析.本研究为对后续隧道病害评价与综合整治以及类似工程的设计提供参考.
1 现场检测
对某既有隧道进行了无损检测, 设置了五条测线,检测采用SIR-3000型便携式探地雷达,该型雷达数字化程度高、探测范围广、分辨率高,并且具有实时数据处理和成像能力,如图1所示.

图1 现场检测图Fig.1 On-site inspection map
雷达反射剖面如图2所示,图2(a)为衬砌与围岩雷达反射剖面示意图,空洞中一般存在空气,围岩、喷射混凝土和二衬与空气的介电常数存在明显差异,因此在时间剖面图上,同相的雷达波错断并向上弯曲,并在混凝土和围岩、空洞之间有明显的界线.图2(b)为空洞雷达反射剖面,当衬砌界面反射信号强,三振相明显,在其下部仍有强反射界面信号,且两组信号时程差较大,可判断此处存在空洞.
通过现场检测发现,在不同里程和隧道不同位置处衬砌界面反射信号强,三振相明显,根据图2(b)判断衬砌背后存在大小不等的空洞,空洞的剖面形状近似呈椭圆状,深度主要分布在0.3~1.5 m,长度约是深度的2倍,与衬砌的距离主要分布在0~1.2 m,如图3所示,此外,通过雷达反射剖面发现部分区段存在二衬厚度不足.
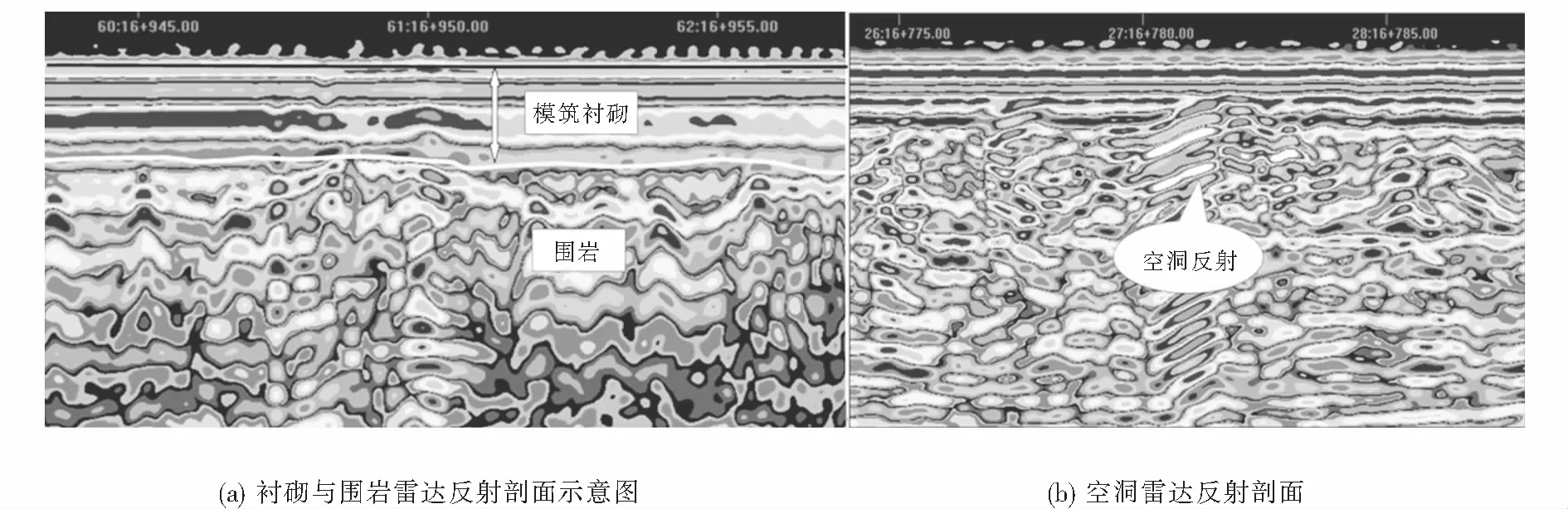
图2 雷达反射剖面Fig.2 Radar reflection profile
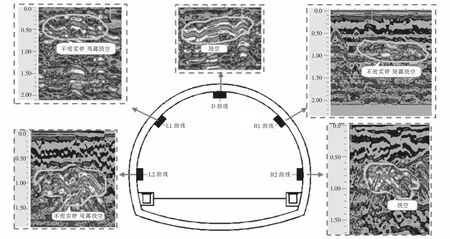
图3 不同位置处空洞雷达反射剖面(单位:m)Fig.3 Radar reflection profiles of holes at different locations (unit:m)
2 数值分析
2.1 数值模型
根据现场检测数据和设计资料,建立数值模型,计算采用“地层-结构”模型,模型顶部为自由边界,两侧边界为水平约束,底边界竖向约束,二衬采用梁单元模拟.模拟计算分7步进行:① 初始应力场分布→② 位移清零→③ 隧道开挖→④ 施作初衬→⑤ 初衬硬化→⑥ 施作二衬→⑦ 出现空洞.衬砌背后空洞通过软件中的钝化单元功能实现.隧道数值模型如图4所示,图4(a)为没有空洞时数值模型,图4(b)为有空洞时数值模型.根据该隧道设计资料确定了围岩和支护结构的相关物理力学参数,如表1所列.
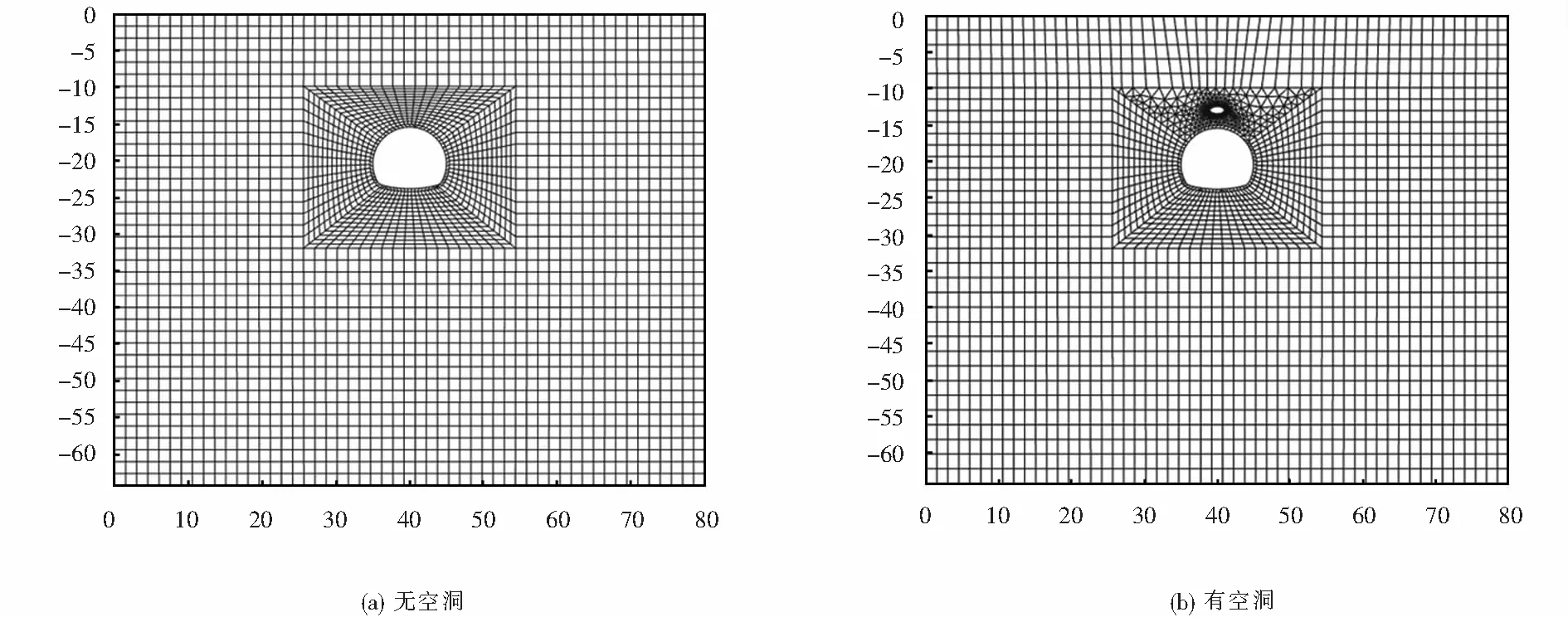
图4 隧道数值模型(单位:m)Fig.4 Numerical model of the tunnel (unit:m)

表1 计算模型物理力学参数Tab.1 Physical and mechanical parameters of the computational model
2.2 结果分析
二衬内力分布如图5所示.图5(a)是施作二衬后轴力分布图,从图可以看出,轴力分布基本均匀,上部均为压力,最大轴力为-45.444 kN,图5(b)是出现空洞后轴力分布图,很明显看出,由于空洞的出现改变了轴力的分布,轴力主要集中分布在拱顶区域,最大轴力为-236.275 kN较未出现空洞时增加了约4.2倍.图5(c)是施作二衬后弯矩分布图,二次衬砌所受的最大正(内侧受拉)、负(外侧受拉)弯矩出现在拱顶和拱腰,分别为9.393 kN·m和-6.541 kN·m,图5(d)是出现空洞后二衬弯矩分布图,很明显空洞的出现改变了弯矩分布,最大正负弯矩分别为10.674 kN·m,-7.544 kN·m,较(c)图分别增加了13.6%和15.3%,甚至在拱顶出现了负弯矩,最大值为-5.241 kN·m.
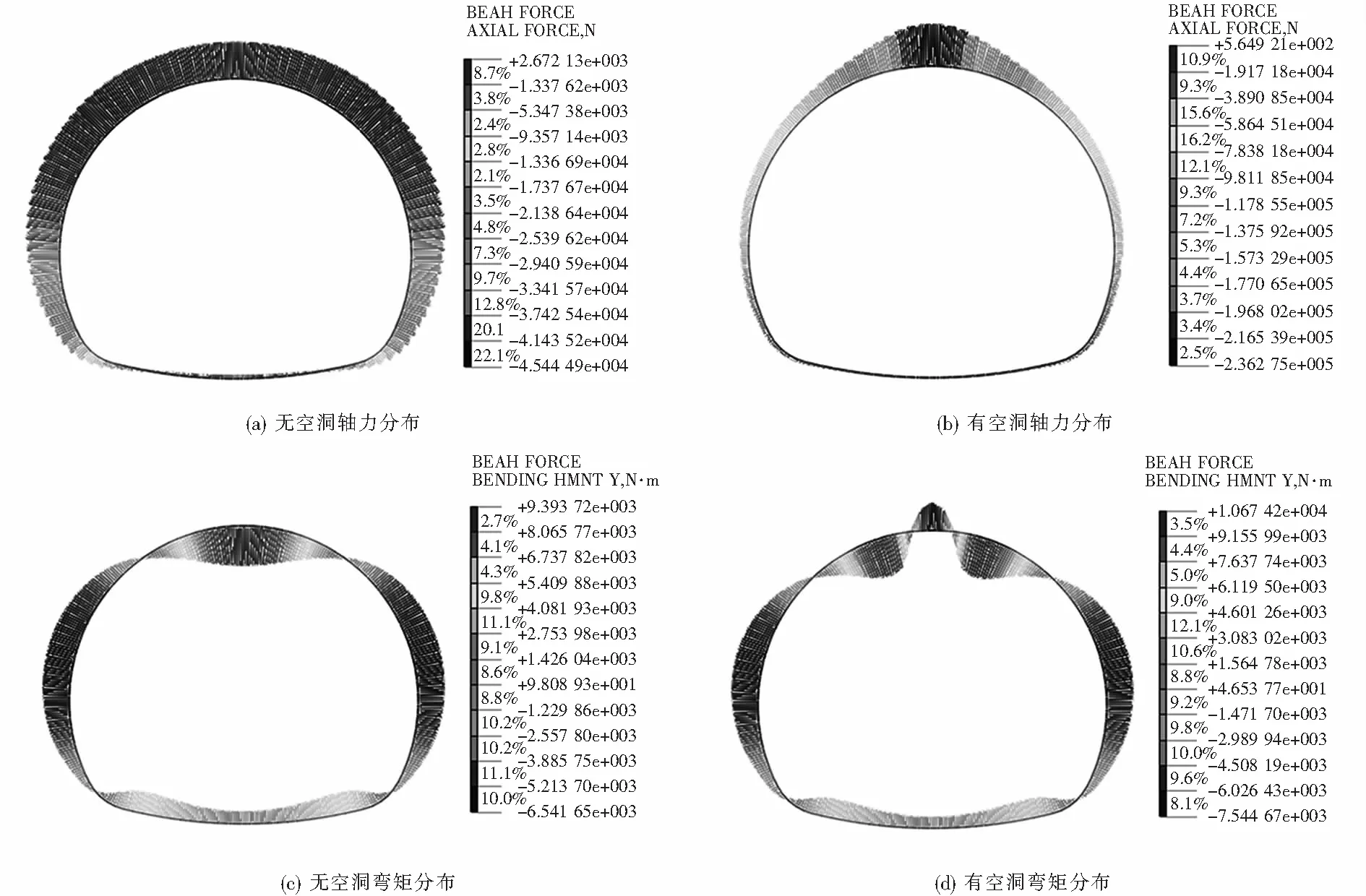
图5 二衬内力分布Fig.5 Internal force distribution of the second lining
用数值分析第⑦步(出现空洞)内力分布减去第⑥步(施作二衬)内力分布,得到了二衬附加内力分布,如图6所示.由图可以看出,空洞的出现导致二衬产生的绝对值最大附加轴力和弯矩分别为-194.812 kN和-16.176 kN·m,出现在拱顶.

图6 二衬附加内力分布Fig.6 Additional internal force distribution of the second lining
上述分析是深1.2 m空洞出现在拱顶,距离二衬1.2 m时得出的结论,很显然,空洞的出现会改变二衬内力的分布,同时产生较大的附加轴力和弯矩,甚至改变弯矩的正负.拱顶区域同时出现正负弯矩,会使拱顶极易产生纵向裂缝,危及行车安全.
3 灰关联分析
根据前文知道,对隧道进行无损检测时在不同里程不同位置出现不同大小的空洞.因此以检测数据和设计资料为依据通过隧道数值模型考虑隧道埋深、空洞深度、空洞距二衬距离和二衬厚度影响因素下二衬附加轴力和弯矩的变化规律,并引入灰色关联理论,分别研究各影响因素与绝对值最大附加轴力和弯矩的关联度.
3.1 灰色关联理论
为了从隧道埋深、空洞深度、空洞距二衬距离、二衬厚度四个变量中分别选出影响二衬最大附加弯矩和轴力的主导因素,本文引入了灰色关联理论进行分析.灰关联分析优势突出,通过对有限数据的分析,可以比较准确地量化比较因素与参考因素之间的关联性(以关联度表示),关联度越大,表明比较因素与参考因素的相关性越强[16].灰关联分析步骤如下:
1) 确定比较列和参考列
本文以影响二衬最大附加弯矩和轴力的各因素(隧道埋深、空洞深度、空洞距二衬距离、二衬厚度)为比较列X,X=[X1,X2,…,Xm]T,分别以二衬最大附加弯矩和轴力作为参考列Y,Y=[Y1,Y2,…,Ym]T,其中,列X、Y的每个因素都有若干值,即Xi=[Xi(1),Xi(2),…,Xi(n)],Yi=[Yi(1),Yi(2),…,Yi(n)],因此列X、Y可写成矩阵形式:
(1)
(2)
2) 矩阵的无量纲化
由于各影响因素的量纲不同,数量级较大,没有可比性,因此必须对Xi和Yi进行无量纲处理.本文采用区间相对值化进行处理,计算方法如下:
(3)

3) 确定矩阵的灰关联差异信息空间,差异矩阵如下:
(4)
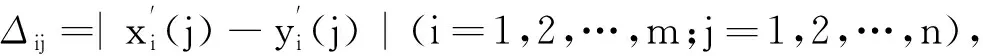
4) 求灰关联系数矩阵与灰关联度
关系系数可以由下式求出:
(5)
式中:ξ为分辨系数,ξ∈[0,1],若越小,关联系数间差异越大,区分能力越强,通常取ξ=0.5.由于关联系数个数比较多,信息比较分散,对比分析较困难,因此通过计算平均值得到关联度来进行影响因素关联性的比较.关联度由下式求得:
(6)
关联度Ai[0,1]为区间内的变化量.关联度序列中影响因素的关联度相对越大,说明该影响因素对既有衬砌最大附加弯矩或附加轴力的影响越大,即其敏感性越大,反之则越不敏感.
3.2 各因素灰关联分析
埋深分别为10 m、15 m、20 m、25 m、30 m时,空洞导致二衬最大附加内力的变化规律,如图7(a)所示.从图可以看出,附加弯矩和轴力的大小与埋深基本呈正相关,埋深从10 m增加到20 m,附加轴力的增长率较附加弯矩高,埋深达到20 m以后,二者基本趋于稳定.随着隧道埋深的增加,衬砌受力趋于稳定,围岩具有一定的自稳能力.
根据无损检测的结果,空洞深度主要分布在0.3~1.5 m,因此在数值计算时空洞深度分别取0.3 m、0.6 m、0.9 m、1.2 m、1.5 m时,研究二衬附加内力的变化规律,如图7(b)所示.从图中可以明显看出,二衬附加内力随空洞深度的增大而逐渐增加,当空洞深度达到1.2 m以后,二衬附加内力急剧增加,附加最大弯矩的增加速率大于轴力.
根据现场无损检测的结果,空洞距二衬距离主要分布在0~1.2 m之间,因此在数值计算中分别取空洞距二衬0 m、0.3 m、0.6 m、0.9 m、1.2 m时,研究二衬附加内力的变化规律,如图7(c)所示.从图可以看出,随着距离的增加,二衬最大附加轴力逐渐减小,而最大附加弯矩逐渐增大,二者的差值先逐渐减小,趋于零以后,差值继续增加并趋于稳定.
二衬厚度分别为30 cm、35 cm、40 cm、45 cm、50 cm时,二衬最大附加内力的变化规律,如图7(d)所示.从图可以看出,二衬最大附加轴力随厚度的增大而缓慢减小,而二衬最大附加弯矩的减小速率较轴力大.当然厚度小的时候,截面积小结构受力小,容易产生裂缝.
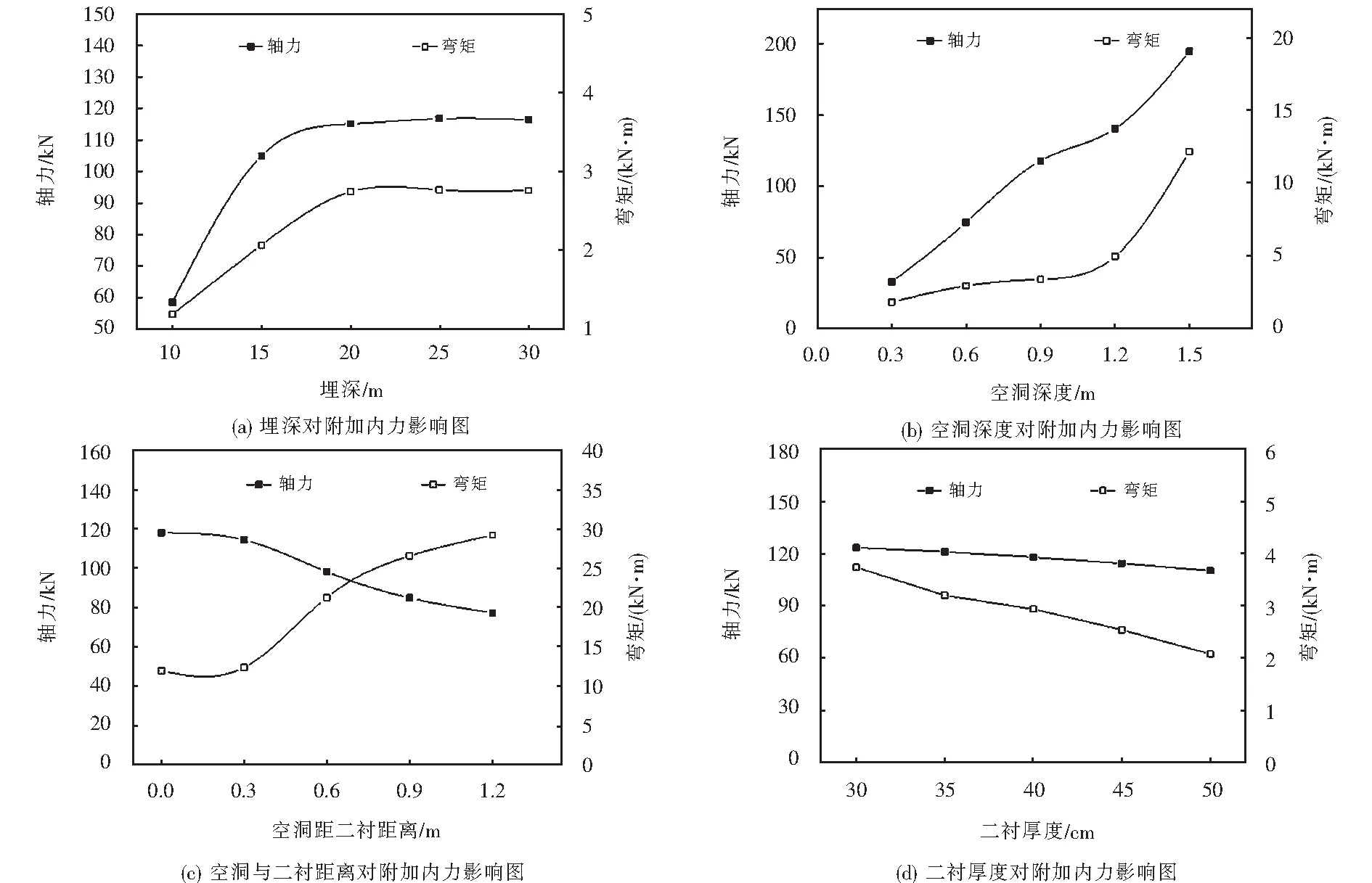
图7 各影响因素下附加内力变化规律Fig.7 Change law of additional internal force under various influencing factors
将以上的数值分析结果利用上述灰色系统理论,可以分别计算各影响因子的附加内力影响程度.建立比较列,参考列如下:
(7)
其中:X1为隧道埋深;X2为空洞深度;X3为空洞距二衬距离;X4为二衬厚度.

(8)
其中:YF为X1,X2,X3,X4所对应的是绝对值最大附加轴力.
YM=
(9)
其中:YM为X1,X2,X3,X4所对应的是绝对值最大附加弯矩.
将以上(7)~(9)式代入式(3)~(6)计算灰色关联度值,得到各影响因子的序列矩阵如下:
AF=[0.729 0.957 0.508 0.504].
AM=[0.768 0.779 0.491 0.537].
关联度值表明,隧道埋深、空洞深度,空洞距二衬距离和二衬厚度对二衬附加内力的影响程度不同.二衬绝对值最大附加轴力影响程度主要取决于空洞深度,隧道埋深次之,空洞距二衬距离第三,二衬厚度次之.二衬绝对值最大附加弯矩影响程度主要取决于空洞深度,隧道埋深次之,二衬厚度第三,空洞距二衬距离次之.后续隧道病害整治应参考影响因素的敏感顺序,为合理有效地提出病害整治方案提供参考.
4 结论
本文借助探地雷达对某既有隧道进行了无损检测,建立相应的数值模型分析了空洞对衬砌受力的影响,同时引入灰色理论对各影响因素进行了灰关联分析.通过分析,得出以下结论:
1) 通过对雷达图像分析,空洞的剖面形状呈椭圆状,深度主要分布在0.3~1.5 m,长度约是深度的2倍,与衬砌的距离主要分布在0~1.2 m.
2) 空洞的出现改变了部分区域弯矩的正负.随着埋深的增大,附加弯矩和轴力不断增大,埋深达到20 m以后,二者基本趋于稳定,随着空洞距二衬距离的增大,附加内力逐渐趋于稳定.
3) 隧道埋深、空洞深度、空洞距二衬距离和二衬厚度四种因素对二衬附加内力的影响程度不同,通过灰关联分析,影响二衬附加内力的主要因素是空洞深度.根据各影响因素的敏感顺序,为后续的病害综合整治提供参考.

