高速公路机电设备使用寿命评估方法研究
周晓旭
(山西省交通科技研发有限公司,山西 太原 030032)
0 引言
我国公路建设发展迅速,公路里程持续增长,截至2018年底,全国高速公路里程达到14万km,公路路网布局日趋合理,公路技术等级和路面等级进一步提高,公路机电设备也日益完善,同时,机电设备在高速公路通车后运营管理过程中的作用也日益显著。高速公路机电设备数量庞大、种类繁多,其运行的安全性和可靠性不仅影响了高速公路日常运营质量和安全效益,更重要的是影响到公众出行和交通的有序运转[1]。
目前,对于高速公路设备的健康状况和养护质量研究更多侧重于设备的故障率和经济寿命,通过开展维修维护的策略研究和折旧分析,确定机电设备经济的报废平衡点和维修方案[2-3]。而在高速公路实际运营和养护管理过程中,机电设备更多是基于故障、实际使用寿命等开展管养活动,检修、更新、报废等往往通过主观判断,养护主要围绕经常性故障的机电设备开展,缺乏数据支撑和科学规划,经济型和合理性欠妥。因此,准确预测机电设备使用寿命不仅能够为科学管养提供数据依据,还能够保障机电设备安全运行,有效避免机电设备故障造成损失,对于高速公路正常有序的运营具有十分重要的意义。
本文以高速公路机电设备使用寿命为研究对象,针对高速公路机电设备使用寿命数据不准和缺少科学计算方法的现状,基于统计学和可靠性的理论,提出一种高速公路机电设备使用寿命预测方法,并以某高速公路收费站摄像机为例,通过拟合AD分布检验、极大似然估计等方法,构建摄像机机电设备故障寿命分布模型,进一步通过K-S检验该数学进行交叉验证,验证本文提出的寿命预测方法的可行性和准确性,并计算出摄像机平均寿命、可靠度和可靠寿命、检修周期等寿命评定指标,基本与收费站摄像机实际经验一致。本方法的提出可为高速公路机电设备的日常检修、更新和报废提供决策依据,降本增效。
1 寿命预测方法研究
1.1 理论基础
机电设备从投入使用到失效的一段时间称为寿命,由于机电设备的失效是随机的,故其寿命不是定值而是随机变量,在工程实践中通常使用概率分布来描述这些随机变量的分布特性。常用描述寿命分布的模型主要有Weibull分布模型、指数分布模型、正态分布模型和极值分布模型等。通常,一个较复杂的机电系统(或设备),在稳定工作时期的偶然失效时间随机变量一般服从指数分布;在损耗期失效服从正态分布;机电设备的疲劳往往呈现对数正态分布或 Weibull分布[4-5]。
1.1.1 Weibull分布模型
三参数Weibull分布的故障概率密度函数和故障寿命分布函数:
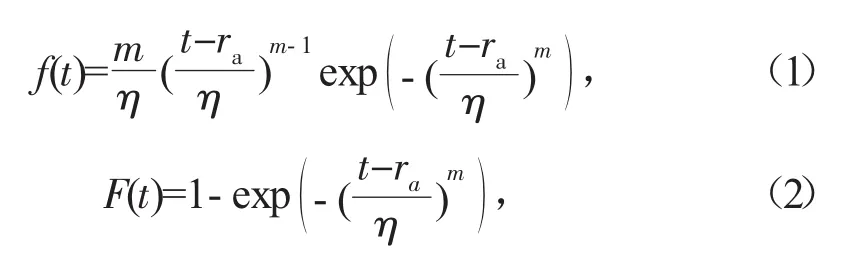
式中:m为尺度参数;η为形状参数;ra为位置参数;t为时间;当 ra为 0时,式(1)、式(2)为两参数 Weibull分布。
1.1.2 指数分布模型
指数分布的故障概率密度函数和故障寿命分布函数:

式中:θ为尺度参数;t为时间。
1.1.3 正态分布模型
正态分布的故障概率密度函数和故障寿命分布函数:
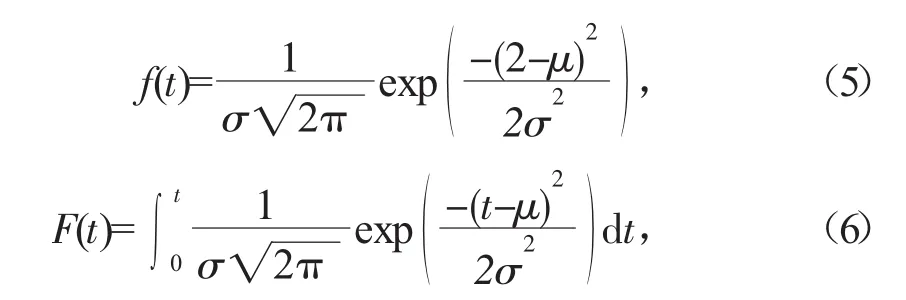
式中:μ为均值;σ为方差。
1.2 数据拟合和分布检验
1.2.1 拟合AD分布检验
拟合AD分布检验是统计学中通过数据拟合的方式检验所收集的数据是否服从某个分布的非参数检验方法,通过计算Anderson-Darling统计量(AD统计量)和p值判断是否符合某目标分布,如式(7)所示。AD统计量其实质是概率图中点离拟合直线距离大小的加权平方和,越靠近分布的尾部,权重越大;AD统计量越小数据分布就越接近目标分布;越大则服从目标分布的可能性就越小。根据AD统计量计算拟合优度检验的p值,如果p值大于0.05,则数据服从目标分布,如果p值小于0.05,则数据不服从目标分布。

式中:AD为AD统计量;i为样本格式;F(ti)为累计故障分布函数;n为样本总量。
1.2.2 参数估计
根据拟合优度分布检验确定最优的故障寿命分布模型,通过参数估计来确定故障寿命分布模型的参数。常用的参数估计方法有矩法估计、最小二乘估计、极大似然估计、贝叶斯估计等,由于高速公路寿命数据通常为不完全样本,需要通过故障寿命分布函数来推断总体故障分布情况。极大似然估计是一种通过似然函数获得总体参数估计的方法,其结果具有无偏性、有效性和相合性等优良性质,被广泛采用,本文选用极大似然估计来进行参数估计。
设总体X=x的概率密度为f(x:θ),其中θ是待估计参数,那么当样本值为x1,x2…xn时,有:
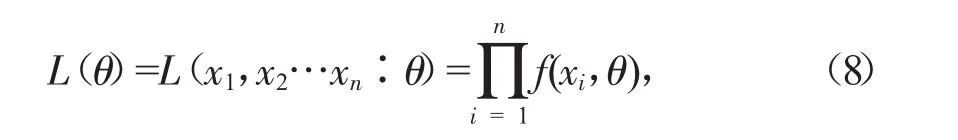
式中:L(θ)称为样本的似然函数。
若满足
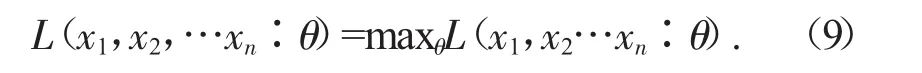
当参数θ=θ*时,似然函数取最大值,那么θ*就叫做参数θ的极大似然估计值。求解似然方程,令:

即可求出θ*值,式中,i为未知参数θ的个数。
1.2.3 检验验证
假设检验主要是用来验证通过参数估计确定的寿命分布函数是否符合真实性。常用的检验方法有K-S检验和卡方检验(X2检验),两种方法都能用来检验一组样本数据的观测经验分布是否与某一已知的理论分布相符合,但X2检验过程受样本数量限制,需要大量样本数据;而对K-S检验不受样本数量限制,也适用于样本数量较少的情况,且该方法对数据的分布类型判定更为敏感,检测效果更佳,在实际中应用较多,本文采用K-S检验来完成对数据的检验验证。
对于给定的样本空间,设样本容量为n,将观测数据按从小到大的顺序重新排列,构造累计频数分布函数Sn(x):
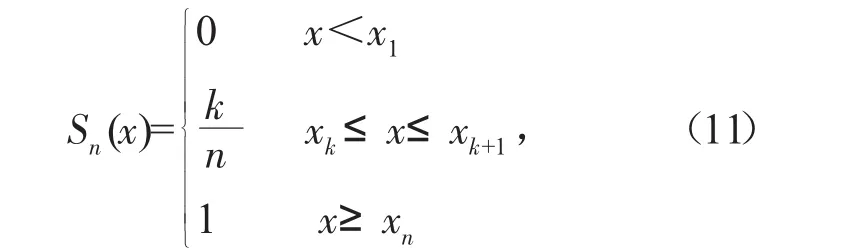
式中:x1,x2…xn为排列后的样本数据;Sn(x)为构造的累计频率函数。
将理论分布累计频数分布函数F(x),构建K-S检验统计量Dn:
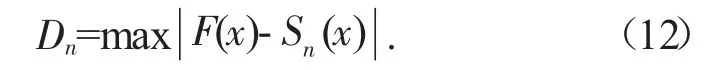
在一定的空间样本n和显著水平α下,通过检验统计量表确定检验统计量临界值Dn*,如果Dn小于Dn*,两个分布函数一致;如果Dn大于Dn*,两个分布函数不同。
1.3 寿命评定指标
高速公路机电设备的寿命评定就是要确定机电设备的平均寿命、可靠度、可靠寿命和更换周期等指标,为机电设备的检修、更新和报废等提供技术依据。
1.3.1 平均寿命
平均寿命是机电设备寿命的平均值或数学期望,主要指机电设备平均能工作多长时间的量。对于高速公路机电设备主要是指平均故障前时间MTTF。
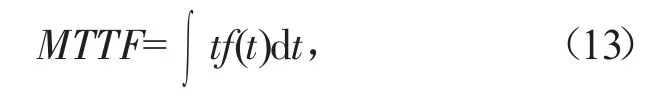
式中:f(t)为故障概率时间分布函数。
1.3.2 可靠度
可靠度是指机电设备平均无故障时间概率。

式中:F(t)为故障寿命分布函数。
1.3.3 可靠寿命
可靠寿命是指机电设备在指定可靠度下所对应的时间,其表达式为:

式中:tR0为可靠寿命;R0为指定可靠度,通常为0.95。
2 应用案例
2.1 寿命预测方法
首先,对机电设备寿命故障数据进行可靠性数据分析和处理,绘制无故障寿命频数分布直方图判断分布是否符合正态分布指数分布、Weibull分布的图形特征;运用Anderson-Darling拟合优度分布检验,计算寿命故障数据与不同寿命分布模型AD统计值和p值,确定与故障数据分布一致的最优故障寿命分布模型;基于极大似然估计法计算故障寿命分布模型对应未知参数,具体为指数分布的参数λ、正态分布的均值μ和标准差σ,Weibull分布的为尺度参数η、形状参数m、位置参数ra;最后通过K-S检验对寿命分布进行交叉检验,验证模型的正确性;并进一步计算各项寿命评定的指标来指导高速公路机电设备寿命评估。
2.2 案例分析
2.2.1 故障数据的处理和分析
本文采用机电设备故障数据为某高速公路5个收费站摄像机日常的养护故障记录,记录时间是从2013年1月至2017年3月,具体摄像机无故障间隔时间的数据统计如表1所示,其中,摄像机无故障间隔时间为摄像机相邻两次故障记录的时间差,并对无故障间隔时间从小到大按升序排列。图1为摄像机无故障数据间隔以N=400 d绘制无故障寿命频数分布直方图,对直方图进行观察,可以得出摄像机无故障寿命频数分布左侧分散,右侧分布集中,基本符合正态分布、指数分布、Weibull分布的特征。
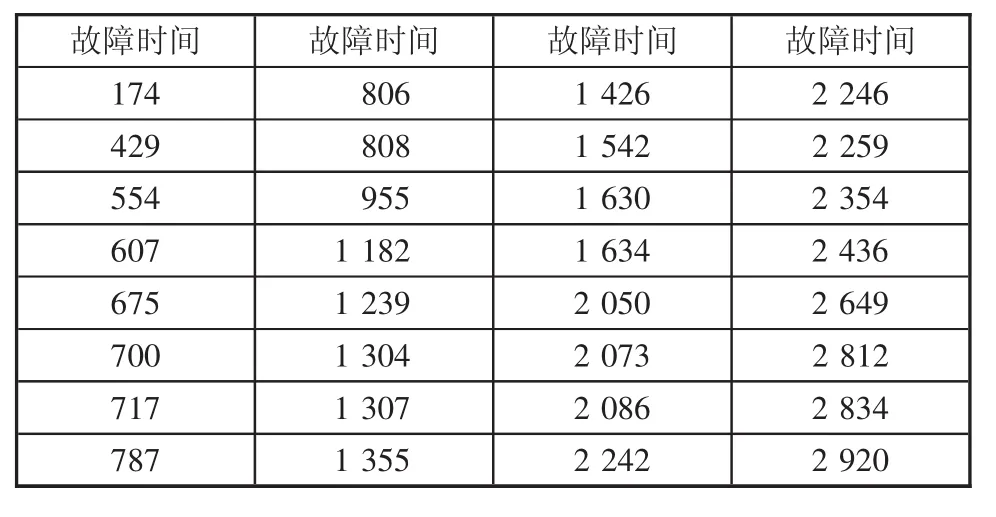
表1 某高速公路收费站摄像机无故障间隔时间统计表 d

图1 摄像机无故障寿命频数分布直方图
2.2.2 拟合优度分布检验
根据式(7)分别对摄像机无故障寿命数据进行正态分布、指数分布、2参数Weibull分布和3参数Weibull分布理论模型的分布拟合,并计算各类分布的AD统计量和p值。表1为AD统计量和p值的计算结果,图2所示为4种分布模型拟合结果的分布概率图。

表2 不同拟合优度分布检验AD统计量和P值计算结果
根据图2,摄像机故障很好地落入正态分布、2参数和3参数Weibull分布的源数据拟合区间95%的置信区间;根据表2,2参数和3参数Weibull分布的AD统计量值最小且相等为0.475,而3参数Weibull较2参数Weibull分布的p值大,且都大于显著水平0.05,表明高速公路摄像机故障寿命数据符合2种Weibull分布模型,且3参数Weibull分布模型更优。
2.2.3 参数估计与寿命分布函数确定

图2 某高速公路摄像机故障数据不同分布模型拟合寿命概率分布图
根据式(8)对高速公路摄像机的故障分布函数进行最大似然估计,计算得到3参数Weibull分布的尺度参数m=1714.9,形状参数η=2.033,位置参数ra=5.88。根据式(2)和式(10),可得摄像机故障分布函数及可靠度函数,如式(16)和式(17)所示,图3为摄像机寿命可靠度函数曲线。
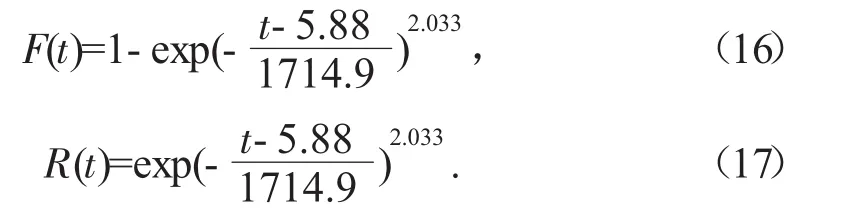
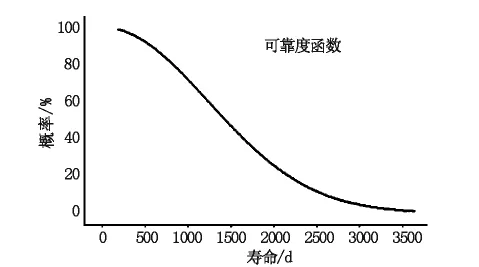
图3 某高速公路摄像机寿命可靠度函数曲线图
2.2.4 检验验证
将某高速公路摄像机无故障寿命间隔数据按300 d间隔进行分组,并对已确定的3参数Weibull分布模型进行K-S检验,检验计算过程如表3所示。
根据表3,K-S检验的统计量观察值Dn绝对值最大值为0.078,在置信水平0.05时,经查表Dn(32,0.05)=0.234>0.078,进一步验证了本文提出 3 参数Weibull寿命分布模型的正确性。
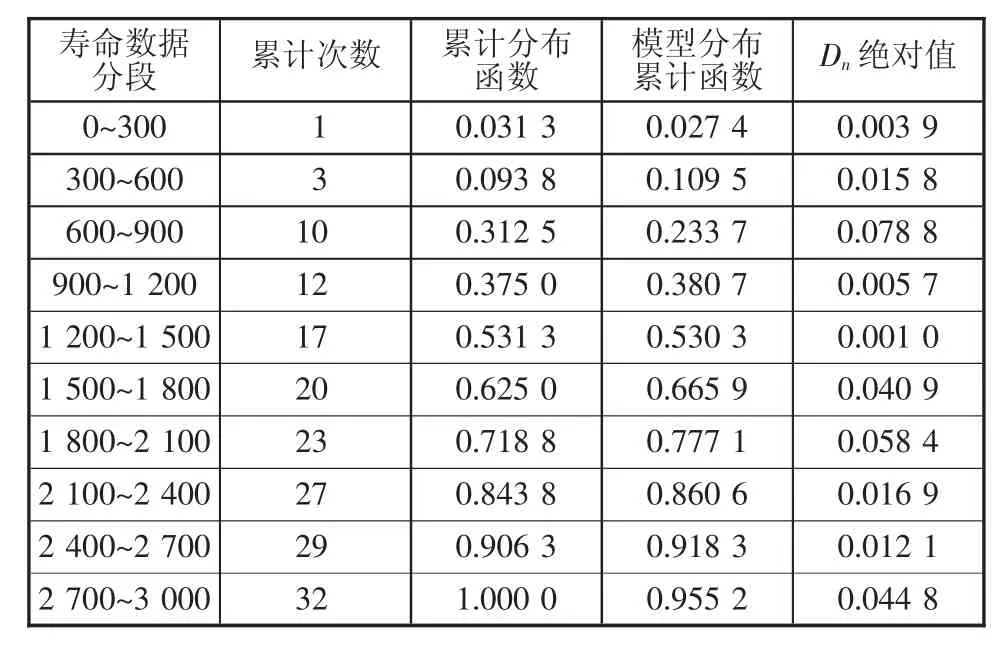
表3 某高速公路摄像机故障寿命分布模型K-S检验计算结果
2.2.5 可靠性评定
根据已确定的3参数Weibull故障寿命分布模型,经式(13)和式(15)计算推导,可得某高速公路摄像机平均寿命和可靠寿命计算公式为:
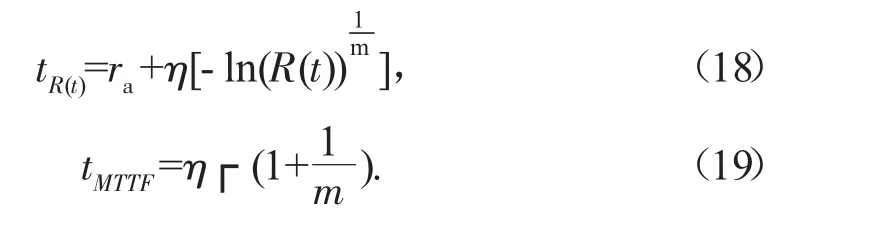
将 η=1717.2,m=2.033 代入式(18)、式(19)在可靠度为0.95情况下,某高速公路摄像机可靠寿命为398.4 d,平均寿命为1 526 d,基本与收费站摄像机实际经验一致。因此,建议每隔0.1tMTTF(153 d)对某高速公路摄像机开展日常检修和维护,每隔398 d在日常点检的基础上对摄像机开展专业检修和状态检测,每隔1 526 d对摄像机进行报废和更新计划的提报。
3 结论
本文从高速公路机电设施运营期养护管理需求出发,针对高速公路机电设备使用寿命数据不准和缺少科学计算方法的现状,提出了一种基于统计学和可靠性的高速公路机电设备寿命预测方法,并以某高速收费站摄像机故障寿命测算为例,通过摄像机日常养护故障数据,建立了符合数据分布特征的寿命分布预测模型,进一步计算出平均寿命、可靠度和可靠寿命、检修周期等寿命评定指标,基本与收费站摄像机实际经验一致。本方法的提出,可为高速公路机电设备的日常检修、更新和报废提供决策依据,降本增效。

