重塑题材渗透方法提升素养

陈艳娇 黄忠仙

摘   要：本文先从核心素养的内涵和学生解决实际问题的现状出发，提出高中物理习题课的目标——如何提高学生的解题素养？然后通过比较原始问题和抽象问题，探讨提高学生解题素养的具体方法：试题习题化和试题原始问题化改造;以及教学中渗透解决物理问题的思维方法。

关键词：解题素养;习题教学;原始问题;思维方法

1  问题提出

物理学科核心素养由“物理观念” “科学思维” “科学探究””“科学态度与责任”四个方面的要素构成。其中作为关键能力的科学思维是具有意识的人脑对科学事物（包括科学对象、科学过程、科学现象、科学事实等）的本质属性、内在规律性及事物之间相互联系和关系的间接与概括的反映，是物理核心素养的核心内容。模型建构、科学推理、科学论证、质疑创新是构成科学思维的四个要素[ 1 ]。

在新课改的引领下，我国基础物理教育取得的成就是不容置疑的，物理教育功能和作用也得到了广泛的认可。但仍存在一个不能忽视的问题：部分学生熟练掌握高中物理知识，也知道物理模型，但遇到新的实际的物理问题无从下手，不懂分析或不会正确分析物理过程，也就无法形成清晰的物理图景，这样在建构物理模型解决物理问题上就遇到困难。这是缺乏解题素养（解题素养包括：审题素养、物理图象素养、状态与过程分析……）一个具体体现。其部分原因跟教学过程中，较注重学生记住物理题型以及利用题型解题的一些经验。题型比较注重某一类习题的外部特征与结论间的直接联系，也就是看见条件就想到结果，对过程分析不做重点考虑，形成固化的、单一因果关系的思维模式，导致遇见没见过的题型，就束手无策。 学生过程分析没有得到提升，对物理模型的理解只是局限于表面，没有从本质进行思考。

物理模型不仅反映原型的直观形象，反映原型的主要特征，抓住了影响事物的主要因素，而且以科学知识和实验事实为依据，经过分析、综合、比较、抽象、概括、推理等一系列严格的逻辑论证建立起来的。学习物理模型的建构对于解决物理实际问题、培养科学思维方法是行之有效的[ 2 ]。如何从物理模型的本源出发，让学生真正了解物理模型的建立过程，提高学生的建模能力，引导学生从“解题”向“解决问题”转变 ，从而提高解题素养是高中物理习题教学需要达到的重要目标之一 。

2  原始问题与抽象问题

原始问题是指自然界与社会生活中客观存在，未经出题者越俎代庖加工的典型物理问题，他只是对现象进行了描述，保持着现实生活中物理情景的原汁原味。与原始问题对应的是经过编制者简化抽象的传统习题（以下称抽象问题）[ 3 ]。如图1所示是原始问题与物理习题间的关系[ 4 ]。

原始问题较抽象问题多了前两个思维过程，因此用原始问題进行学习。首先要对实际问题进行加工，梳理哪些是主要因素，哪些是次要因素？将实际问题转为抽象问题，从而实现实际情景向理想模型的过渡，可以帮助学生实现理想化模型的建立。建立物理模型的过程中，要结合多种思维，因此解决原始问题的过程也是思维培养的过程，建模能力和抽象思维能力同时会得以提升。

当然抽象问题也是有很多可取之处：有利于物理概念和规律的巩固;抽象问题侧重于计算和推导，对培养学生的逻辑思维是有利的;抽象问题答案唯一性特点，也有利于对学生进行统一的考察和评价。

对学生科学素养的培养而言，如何让原始问题与抽象问题优势互补，应成为物理习题教学的基本出发点。笔者认为对传统的高考试题进行设计改编使之习题化、原始问题化不失为一条有效途径。

3  核心素养视角下高中物理习题教学

3.1  重塑高考试题

3.1.1  高考试题习题化

习题的功能是建构和培养能力，是训练让你会。而高考试题的功能是用于招生选拔的甄别，是考你会不会。所以高考试题内容散乱、没有合理思维线索;能力跨度大、缺乏循序渐进;重结果，轻过程，缺乏解决问题过程的引导。因此应用高考试题作为习题教学素材应先将其习题化改编，如将选择题该为有梯度的简答题。

2009年高考试题（江苏省）：如图2所示，两质量相等的物块A、B通过一轻质弹簧连接，B足够长、放置在水平面上。所有接触面均光滑。弹簧开始时处于原长，运动过程中始终处在弹性限度内。在物块A上施加一个水平恒力，A、B从静止开始运动到第一次速度相等的过程中，下列说法中正确的有（      ）。

A.当A、B加速度相等时，系统的机械能最大;

B.当A、B加速度相等时，A、B的速度差最大;

C.当A、B加速度相等时，A的速度达到最大;

D.当A、B加速度相等时，弹簧的弹性势能最大;

改为练习题：如图2所示，光滑水平面上，放两表面均光滑的物块A、B，其中物块B足够长。物块A、B的质量均为m，通过一轻质弹簧连接。弹簧开始时处于原长，现在物块A上施加一个水平恒力F，接下来的运动过程中弹簧始终处在弹性限度内。求：

（1）初始时刻两物块的加速度分别为多少？物块A加速度为零时。物块B的加速度为多少？任何时刻两物块加速度关系如何？

（2）从静止开始运动，物块A的加速度如何变化？从静止开始运动到物块A加速度为零过程，物块A的速度如何变化？画出对应的v-t图象。

（3）从静止开始到物块A加速度第一次变为零过程，物块B的加速度与速度如何变化？画出对应的v-t图象。

（4）何时两物块的相对速度最大？何时两物块的相对位移最大？

（5）从开始到物块A加速度为零过程，两物块速度变化量的大小关系如何？（提示从加速度的关系特点考虑）

改编后的习题围绕提升“状态与过程分析”和“图像素养”进行设计：

①两物块的受力分析（第1小题）;

②两物块的状态与过程分析，并理解图象斜率的意义（第2和第3小题）;

③根据图象，理解图象纵坐标和面积的意义（第4小题）;

④利用加速度变化对称的思想，及微积分思想分析推理（第5小题）。

3.1.2  高考试题原始问题化

经抽象处理后的传统高考试题不利于学生的建模意识及对信息“抽丝剥茧”的科学思维的培养。那么如何将高考试题改编成原始问题习题呢？我们可以拆除试题中“抽象”和“理想化”的框架，甚至拆除确切的数据，注入常见的生活元素或真实的物理事件、物理学史等[ 5 ]。

2007年高考试题（全国卷）：甲、乙两运动员在训练交接棒的过程中发现：甲经短距离加速后能保持9m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀速的，为了确定乙起跑的时机，需要在接力区前适当的位置标记。在某次练习中，甲在接力区前x0=13.5m处作了标记，并以v=9m/s的速度跑到此标记时向乙发出起跑口令，乙在接力区的前端听到口令时起跑，并恰好在速度达到与甲相同时被甲追上，完成交接棒。已知接力区的长度为l=20m，求：

（1）此次练习中乙在接棒前的加速度a;

（2）在完成交接棒时乙离接力区未端的距离。

改编题：接力赛跑属于多人合作的项目，堪称田径比赛的重头戏，交接棒环节的发挥往往能左右最终的名次。交接棒过程，当拿着棒的运动员快接近接力区时，将要接棒的运动员便开始起跑，以便达到最大速度时完成接棒。如果运动员站出跑道或者已离开接捧区时仍未完成接棒，全队会将被取消比赛资格。请分析顺利接棒情况下如何使交接棒时间最短？

为解决这个问题，学生首先就要考虑其他问题（如：运动员的最大速度多少？运动员做什么运动？在哪里完成接力耗时最短？等） 这样学生不仅可以注意到平常做题中题目已给定条件，而被忽略的细节。通过这样训练，学生在思考问题的时会更细致、深入。思维能力也会逐渐的增强，建模和化简意识逐渐形成和提高。

当然原始问题的编制和教学策略根据不同的培养目标有所不同，这点可以通过实践探索积累经验或借鉴同行的经验，如：《新课标下中学物理原始问题设计策略》[ 5 ]和《原始问题下对生物习题设计的思考》[ 6 ]。

3.2  渗透思维方法

解决问题的能力不同于运动的动作技能，对于动作技能可以通过大量的机械训练得到强化，而大量的机械训练只会使学生的思维钝化。解决问题的能力需要转化、推理、分析、综合、创造等心理行为，他需要学生深入思考、领悟、总结才能得以提升。在不同情境展现相同的解决问题的思维操作过程，使思维方法在不断渗透中感悟掌握。

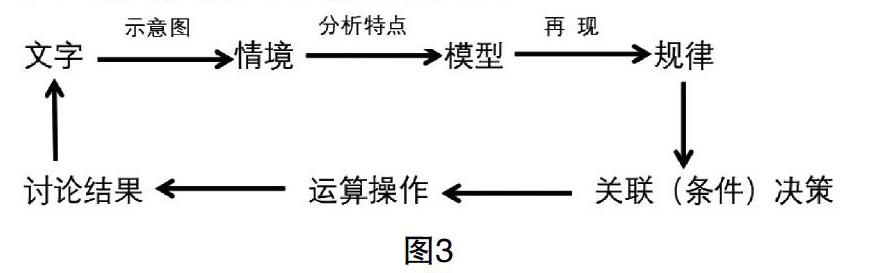
物理问题解决的思路有三个环节：（1）模型分析，包括：对象模型、环境模型和过程模型;（2）特定条件分析，对于原始问题需要挖掘隐含条件或合理设定条件;（3）根据模型规律和特定条件所要求的计算方法解决问题。用一个步骤图（如图3）来清楚地表示：

下面就以上的改编题为例说明问题解决的思路：

（1）根据文字化示意图呈现情境如图4所示;

（2）构建模型：

①对象模型：分析对象拿棒运动员（运动员甲）和接棒运动员（运动员乙），我们研究是交接棒的时间问题，因此两运动员可抽象为质点;

②环境模型：运动员在起跑过程中空气阻力的变化可以忽略，抽象认为受到合外力恒定;

③过程模型：通过分析两运动员的初状态和加速度，运动员甲可看做匀速直线运动，运动员乙在起跑过程做初速度为零的匀加速直线运动。

（3）规律：找匀速直线与匀变速直线运动相关的规律;

（4）关联条件：

①时间关联：忽略声音在空气中传递时间，运动员甲从A运动到C的时间，等于运动员乙从B运动到C的时间;

②空间关联：根据示意图找两运动员位移关系。

（5）边界（临界）条件：运动员乙从起跑到接棒的位移应不大于接力区的总长度。

（6）运算操作：结合规律方程与条件关系，合理设定运动的最大速度、加速度及接力区的长度进行运算操作;

（7）讨论结果：分析接棒的最短时间。

由于交接棒的最短时间受多种因数的影响，如：两运动员的最大速度大小关系，运动员加速度大小，运动员乙起跑时两运动员的距离等。原始问题学生有独立的设置问题空间，没有唯一的正确答案。因此在问题讨论的最后，我们可以呈现原试题的具体数据进行分析计算。

习题教学不仅是进一步认识巩固物理概念和规律，学生要能在问题的分析过程中形成正确的思维习惯和科学态度，从而提高解决实际问题的能力。以原始问题习题化的高考试题作为教学的素材，老师在分析问题和解题示范過程中渗透的思维方法，有利于学生思维能力科学而有效的发展，从而提升学科核心素养。

参考文献：

[1]中华人民共和国教育部.普通高中物理课程标准（2017年版[S].北京：人民教育出版社，2018.

[2]薛进.模型建构方法在生物教学中应用例析[J].佳木斯教育学院学报，2012（11）：272-273.

[3]朱玉成，刘茂军，肖利.物理课堂引入原始问题的可行性分析与策略初探[J].物理教师，2013（3）：6-8.

[4]刑红军.原始问题教学：物理教育改革的新视域[J].课程·教材·教法，2007（5）：53-59.

[5]高夏琼，李松岭.新课标下中学物理原始问题设计策略[J].湖南中学物理，201（8）：64-66.

[6]欧阳和和.原始问题下对生物习题设计的思考[J].中学生物学，2014（7）：45-46.