形符表征数学概念的三种形式
摘 要 表征数学概念时可以应用丰富的数学化的学具、图像、数学符号等形符元素,并呈现出三个层次:动作性形符表征能让数学概念可感、图像式形符表征能让数学概念可视、符号化形符表征能让数学概念可思。有效转译学生数学思维的表征过程,可以促进数学概念的深度理解。
关键词 动作性形符 图像式形符 符号化形符 表征 数学概念
表征是信息在心理活动中表现和记载的方式,既是认知过程,也是认知结果。布鲁纳指出,学生对新知识的加工过程分为行为表征、图像表征和符号表征三个阶段。在新知识教学过程中会遇到大量的数学概念,这些数学概念的表征能力和理解水平直接影响着学生后续的学习品质。数学概念的表征有着不同的路径,其中,数学化的操作学具、直观图像、抽象符号等形符元素的表征效度,直接影响着不同层次的学生对数学概念的加工与理解深度。
由此,下面以苏教版《数学》二年级上册“认识线段”为例,围绕形符表征线段概念的三种形式进行教学解读与思考,与大家共同分享与探讨。
一、动作性形符表征,让数学概念可感
抽象性和概括性是数学概念的基本特征。概念的心理表征需要通过外部表征来输入或输出,对学生的概念理解带来了挑战。通过身体动作表征认知客观世界是人与生俱来的遗传本能。皮亚杰指出,主体动作是一切经验和知识的源泉,并将儿童思维的发展划分为感知运动、前运算、具体运算和形式运算四个阶段。很多时候学生要借助对具体实物或数学化替代物进行实际操作,在具身的动作体验中触发数学思维、提升理解水平,因此动作性形符表征能让数学概念可感。
线段是为了数学表达或研究的需要,从生活实物或社会现象中高度抽象出来的数学模型。为了更好地理解线段概念,笔者设计了三次动作性形符表征活动。
活动1:你能想办法把桌上弯曲的毛线变直吗?
交流揭示:像这样,把线拉直,两手之间的一段可以看成线段,两手分别看作这条线段的开始和结束。
学生上台展示自己拉出的线段(长短、粗细、方向、颜色不尽相同)。
活动2:你有什么好办法把自己创造出的线段“请”到黑板上去吗?
交流并操作:用两个吸珠分别替代左、右手,把线段“吸”在黑板上。
追问:两个吸珠间的一段为什么都可以看成线段?
小结:它们都是直的、有两个端点,与线的长短、粗细、方向、颜色等无关。
……
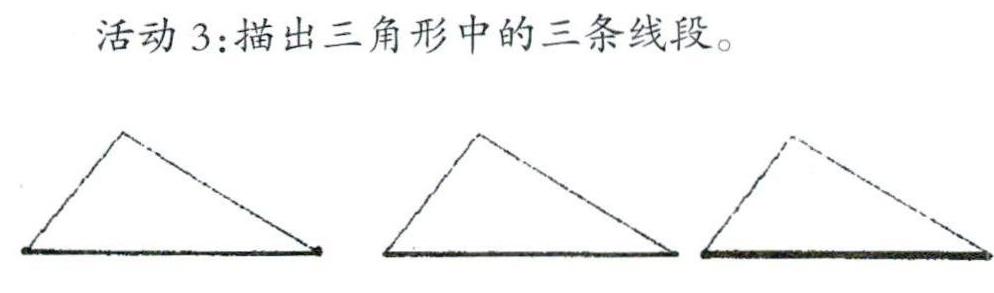
活动3:描出三角形中的三条线段。
交流:描哪条线段时最轻松?
小结:线段有长短。
聚焦:要描的线段是一样的,但描出来的线段为什么有粗有细?
小结:线段无粗细,笔有粗细。
第一次操作是基于教材例题编排的毛线拉直活动,动态揭示线段的描述性定义,动作感知线段的特征“直”且“有始有终”。第二次的吸珠操作,形象地将两手与端点进行嫁接,有效排除长短、粗细、方向、颜色等非本质属性,聚焦线段外显特征“两个端点”和“直”。值得注意的是,“两个端点”并非线段的本质特征,只是为了清晰地表征出“有始有终”,意即“线段有长短”。第三次的描线段活动更是深刻地体验了线段的本质属性“线无粗细”和“线段有长短”。于是,一系列外在动作性形符表征的知觉活动催生内隐的数学思维,动作感知点加深了概念知识点与技能点的数学理解,线段概念逐层得到清晰内化与深层建构。
二、图像式形符表征,让数学概念可视
小学生以形象直观思维为主的认知规律,表现为不同层次的思维水平。郑毓信认为,学生思维活动的水平主要取决于外在刺激的程度,对此区分出动作的、图像的、符号的三个不同的表征水平,其中图像表征是指具体物消失时学生能依据实物的影像在头脑中制作心像来进行内在的思维活动[1]。特别地,三种表征水平并非纯粹线性关系,完全割裂,体现为相伴相生、辩证融合,共同作用并服务于数学学习。外化的图像式形符表征既能刺激学生内在的心智活动,也是学生头脑中心像的具体化表达,直观理解概念,实现数学概念的思维可视。
例如上述教学片断中,“毛线拉直”时学生“看见”了线段图像的雏形,吸珠活动则在头脑中表征生成半抽象式的线段图象,而描三角形中的线段直观呈现图式,体悟“线段无粗细”“线段有长短”的抽象内涵。
在进一步抽象出线段的符号模型之后,笔者设计了两次在頭脑中制作心像的内在思维活动。
活动1:请大家闭眼想象一下线段的样子,你在脑海中“看到”了什么?
学生闭眼想象、交流分享。
师:请大家睁大双眼看向老师,有没有发现此时在你和我的双眼之间就有一条线段?
学生想象、思考,慢慢地爆发出“看见了,我看见线段了”的声音。
交流小结:一个端点是老师的眼睛、另一个端点是自己的眼睛,两个端点之间的目光是直直的,形成一条线段。
活动2:当老师走近一点、再走近一点,或者走远一些、再走远一些,你有什么发现?
生:我和老师两眼之间的线段变短或变长了。
图像式形符表征可以分为两类,一类是外显可视的直观图像,一类是内隐制作的心智图像。它们通过现实视觉或虚拟视觉,促进概念理解。闭眼活动,学生在头脑中固化并强化了线段的图像模型。睁眼行动,则脱离具体的实物与模型,借助想象展开内在思维活动,在脑海中从“有形”走向“无形”,“看见”老师和学生之间“无形又有形”的线段,既体现数学学习有趣、有意思,又进一步体会“线段无粗细”“线段有长短”,实现线段概念的意义认知与深度抽象。
三、符号化形符表征,让数学概念可思
数学符号是在数学理解的基础上抽象而成的,符号化表征体现数学学习的高阶思维。张奠宙在《小学数学教育概论》中表示:数学概念是客观世界中数量关系和空间形式的本质属性在人们头脑中的反映,它是用数学语言和符号揭示事物共同属性的思维形式。然而,“基于概念本身、学生的年龄特征、心理特征及学习水平,在小学阶段有许多概念难以说得清、道得明,甚至只能意会难以言传,或者有些严谨的术语对学生而言理解难度较大,所以一些概念不宜定义或难于定义”[2]。此时,符号化形符表征概念便能实现与动作性形符表征、图像式形符表征之间的自由转换。
例如教材例题直接给出了线段的符号化形符,传递出线段概念的清晰样态。所以,先让学生画出心中的线段,自主调取线段的个性化理解,实施思考与表征,端点的表示方式只是形式化的表达,外化出来的既是线段的图像式表征、又是线段的符号化表征。
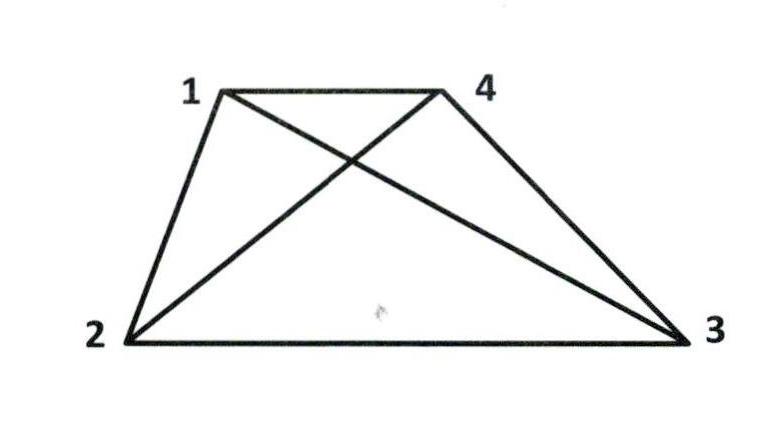
再如“想想做做”第5题:在两点之间画一条线段,你能画出几条?
观察思考:如何连线不易重复和遗漏?
交流连线:给4个点分别标上序号1、2、3、4,有序连出线段。
思考讨论:如何记录表达你连出的所有线段?
集体交流:线段1-2、线段1-3、线段1-4、线段2-3、线段2-4、线段3-4。
上述教学片断,学生经历了两次符号化形符表征的历程,接受了两次数学思维的冲突与考验,彰显了符号化思想。第一次冲突是为了言语表达与有序连线的需要,四个点用1、2、3、4符号化命名,带来思维便利,并且与4个数中选两个组成两位数建立图式关联,实现了第一次平衡。第二次冲突是如何清晰记录并表达所连6条线段,实现了将思考过程从言语表征向符号表征的转译,完成意义重组。类似“线段1-2”的符号化形符表征的形态虽然不尽完美,但却是学生运用数学符号进行的思维操作,实现了思维有序,并且传递着线段“从点1始、至点2终”的数学概念信号,标志着主体思维已经能达到较高的抽象水平。
事实上,三类思维水平层次的动作性形符表征、图象式形符表征、符号化形符表征在不同的学习阶段体现不同的应用价值,只有因需要而选、因适合而用,才能降低学生的认知负荷,从而提升教学实效,促进学生数学思维的有序发展。
参考文献
[1] 郑毓信.多元表征理论与概念教学[J].小学数学教育,2011(10).
[2] 姚建法.例谈小学数学描述性概念的教学[J].教学与管理,2015(20).
[责任编辑:陈国庆]
该文为江苏省中小学教学研究第十二期重点资助课题“重建儿童课堂生活——基于‘诗意儿童文化的童性课堂研究”(2017JK12-ZA07)、江苏省教育科学“十三五”规划重点资助课题“苏教版小学数学教材例题中多元表征的教学研究”(B-a/2020/02/06)的阶段性成果

