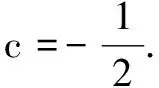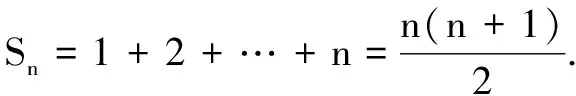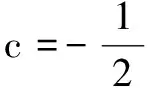应用导数求一类数列前n项和

敬加义 黄超英 余胜蓝

(四川省绵阳市开元中学，621000)

若数列{an}是等差数列,数列{bn}是等比数列,则称数列{anbn}为差比数列.此类数列的前n项和,是高考和高考模拟考试中的高频题,老师们千篇一律地教给学生的解法是“错位相减法”.本文另辟蹊径,给出差比数列求和的导数方法,不妨看作导数在中学数学学习中的另一种应用.

一、理论探究

当x≠1时，根据等比数列前n项和公式,有

①

①式两边分别对x求导,可得

1+2x+…+nxn-1

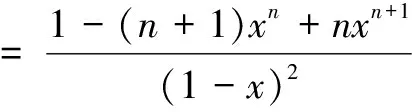
②

在差比数列{an}中,设an=(λn+μ)xn+m(λ、μ、m∈R,λ≠0,n∈N*)，则有an=λnxn+m+μxn+m=λxm+1·nxn-1+μxn+m,故

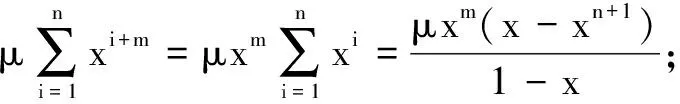
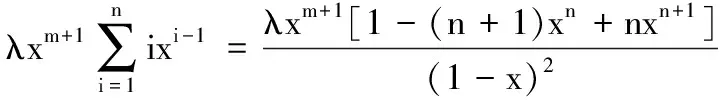
两式相加，整理可得

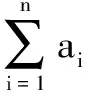
-(λn+λ+μ)xn+m+1

+(λn+μ)xn+m+2].

③

二、应用举例

利用(3)式，可迅速解决差比数列前n项求和问题.下面举例说明.

例1(2016年山东高考题)已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.

(1)求数列{bn}的通项公式;

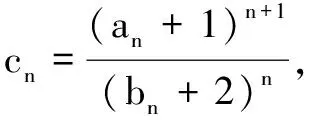
解(1)an=6n+5;bn=3n+1.(过程略)

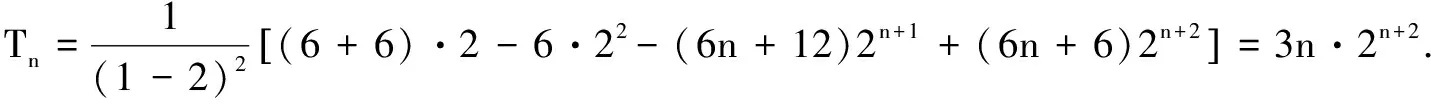
例2(2015年湖北高考题)设等差数列{an}的公差为d,前n项和为Sn,等比数列{bn}公比为q,已知b1=a1,b2=2,q=d,S10=100.

(1)求数列{an}、{bn}的通项公式；

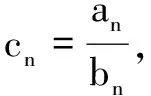
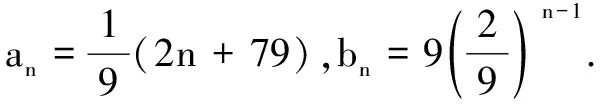
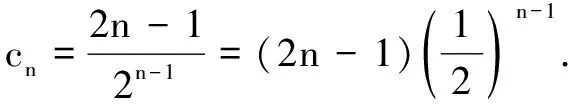
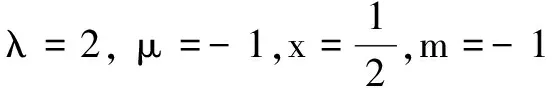
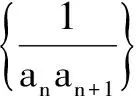
(1)求数列{an}的通项公式;

(2)设bn=(an+1)2an,求数列{bn}的前n项和Tn.

解(1)an=2n-1.(过程略)

(2)由(1)知bn=2n·22n-1=n4n.

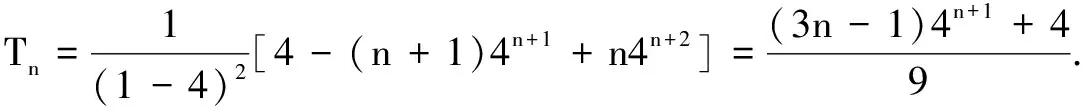
例4(2014年全国高考题)已知{an}是递增的等差数列,a2、a4是x2-5x+6=0的根.

(1)求{an}的通项公式;

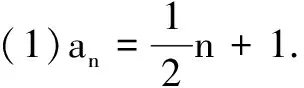
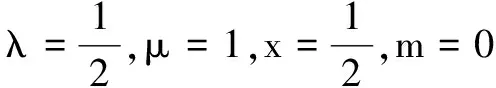
由上可见，公式③为差比数列求和提供了一种求解通法，实际解题时只需按③式推导过程进行整理，可使问题获解.下面提供一组高考题作为变式，供大家参考.

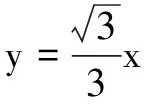
(1)证明:{rn}为等比数列;

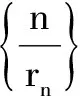
提示(1)略

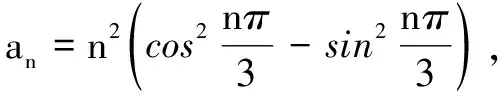
(1)求Sn;

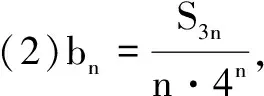
提示(1)

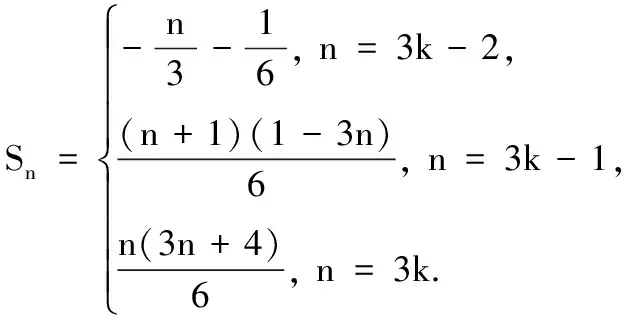
变式3(2005年湖北高考题)设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.

(1)求数列{an}和{bn}的通项公式;

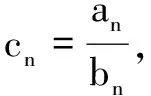
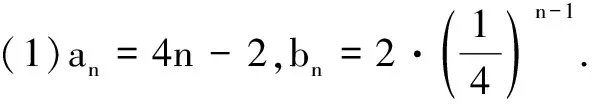
(2)由(1)可知cn=(2n-1)4n-1.

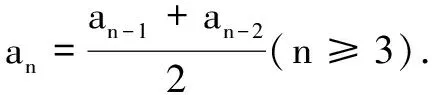
(1)求c的值;

(2)求数列{nan}的前n项和Sn.