一道空间解几题的函数解释

金 莹

(广东省佛山市南海中学，528211)

一、试题剖析

在2020年1月的佛山市高二年级统考中,一道填空压轴题难倒了很多考生.该题具有一定的空间解析几何的背景,体现了命题者的创新性,深刻考查了学生的思维能力.

试题在棱长为2的正方体ABCD-A1B1C1D1中,点P是正方体棱上一点,|PB|+|PC1|=λ.

(1)若λ=4,则满足条件的点P的个数为______;

(2)若满足|PB|+|PC1|=λ的点P的个数为6,则λ的取值范围是______.

反思回顾对该题的思考,很多学生和老师都联想到了橄榄球模型,但空间想象力不够导致很难跨越障碍;也有软件高手动态演示了本题,但考场上无法借助这些先进的信息技术辅助解题.那么,这道题能用学生更容易理解的方法去解释吗?

笔者研究发现,点P在正方体棱上的位置确定了,则相应的实数具有唯一确定的值与之对应.换句话说,可以从函数值域的角度来对问题进行解释.现整理成文,与大家分享.

解先计算正方体的8个顶点到B、C1两点的距离之和 (如图1).

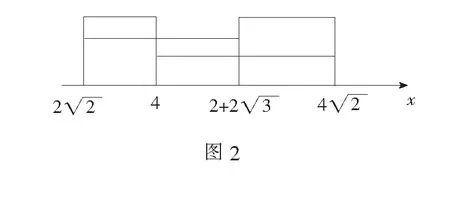
由几何直观,可以发现在每条棱上|PB|+|PC1|=λ是单调递增的.于是

评注根据图2,还可以得出如下结论:若满足|PB|+|PC1|=λ的点P的个数为4,

如果我们把椭圆的焦距改为体对角线BD1,可得上述试题的如下一个变式题.

变式在棱长为2的正方体ABCD-A1B1C1D1中,点P是正方体棱上一点(不包括棱的端点),|PB|+|PD1|=λ.

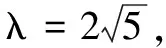
(2)若满足|PB|+|PD1|=λ的点P的个数为6,则λ的取值范围是______.

提示仿原式题解法,可得参考答案如下:

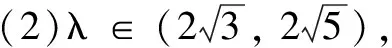
二、教学思考

文[1]中提到“对于理性思维的考查,突出体现在综合分析问题的过程之中,通过复杂情境的设计增强题目综合性,考查学生是否能够根据已知信息,从合理的角度思考问题,用合理的方法解决问题.”本题把学生熟悉的椭圆定义镶嵌在正方体模型中,使得问题情境复杂化，体现了问题的综合性，加强了理性思维的考查.第(1)问可以靠着空间感猜出来,但第(2)问没有正确的方法是很难碰撞出来的.这就提醒我们平时的教学中应注重培养学生的观察力,先从特殊位置(端点)入手,将问题逐步转化为熟悉的情境(函数值域),构建合理的数学模型解决问题.这实际上是对学生逻辑推理、直观想象、数学抽象、数学建模等关键核心素养的综合培养和运用.