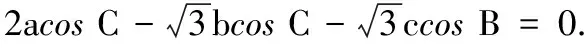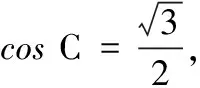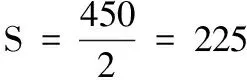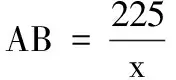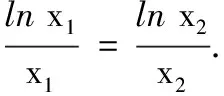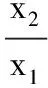高三数学综合测试
一、填空题(本大题共14小题,每小题5分,计70分)
1.集合A={x|x=2k-1,k∈Z},B={1,2,3,4},则A∩B=______.
2.已知复数z=a+bi(a、b∈R),且满足iz=9+i(其中i为虚数单位),则a+b=______.
3.某校高二(4)班统计全班同学中午在食堂用餐时间,有7人用时为6分钟,有14人用时7分钟,有15人用时为8分钟,还有4人用时为10分钟,则高二(4)班全体同学用餐平均用时为______分钟.
4.函数f(x)=(a-1)x-3(a>1,a≠2)过定点______.
5.等差数列{an}(公差不为0),其中a1,a2,a6成等比数列,则这个等比数列的公比为______.
6.小李参加有关“学习强国”的答题活动,要从4道题中随机抽取2道作答,小李会其中的3道题,则抽到的2道题小李都会的概率为______.
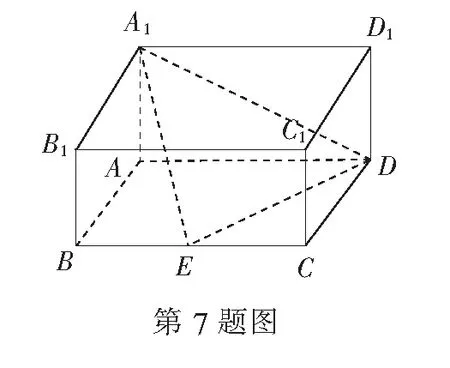
7.在长方体ABCD-A1B1C1D1中,点E为BC的中点,AB=1,AD=2,AA1=1,则点A到平面A1DE的距离是______.
8.在如图所示的流程图中,输出n的值为______.
9.圆C:(x+1)2+(y-2)2=4关于直线y=2x-1的对称圆的方程为______.


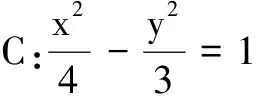
12.对于任意的正数a、b,不等式(2ab+a2)k≤4b2+4ab+3a2恒成立,则k的最大值为______.
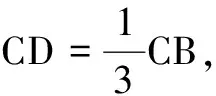
14.函数f(x)=|x2-1|+x2+kx+9在区间(0,3)内有且仅有两个零点,则实数k的取值范围是______.
二、解答题(本大题共6小题,计90分.解答时应写出文字说明、证明过程或演算步骤)
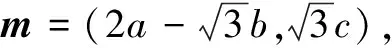
(1)角C的大小;

16.(本小题满分14分)在四棱锥P-ABCD中,底面ABCD是平行四边形,O为其中心,∆PAD为锐角三角形,且平面PAD⊥底面ABCD,E为PD的中点,CD⊥DP.
(1)求证:OE∥平面PAB;
(2)求证:CD⊥PA.


(1)求∆PF1Q的周长;
(2)求∆PF1M面积的最大值.

18.(本小题满分16分)一酒企为扩大生产规模,决定新建一个底面为长方形MNPQ的室内发酵馆,发酵馆内有一个无盖长方体发酵池,其底面为长方形ABCD(如图所示),其中AD≥AB.结合现有的生产规模,设定修建的发酵池容积为450米3,深2米.若池底和池壁每平方米的造价分别为200元和150元,发酵池造价总费用不超过65 400元.
(1) 求发酵池AD边长的范围;
(2)在建发酵馆时,发酵池的四周要分别留出两条宽为4米和b米的走道(b为常数).问:发酵池的边长如何设计,可使得发酵馆占地面积最小.


(1)求数列{an}、{bn}的通项公式;

20.(本小题满分16分)设函数f(x)=lnx-ax,a∈R,a≠0.
(1)求函数f(x)的单调区间;
(2)若函数f(x)=0有两个零点x1、x2(x1 (i)求a的取值范围; (1)求直线OC与DE所成角的余弦值; (2)求二面角A-DE-C的正弦值. 参考答案 一、填空题 1.{1,3};2.-8;3.7.5;4.(0,-2); 二、解答题 16.(1)连BD.因为ABCD为平行四边形,O为其中心,所以,O为BD中点. 又因为E为PD中点,所以OE∥PB. 又PB⊂平面PAB,OE⊄平面PAB, 所以,OE∥平面PAB. (2)作PH⊥AD于H,因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PH⊥AD,PH⊂平面PAD,所以,PH⊥平面ABCD. 而CD⊂平面ABCD,所以CD⊥PH. 又CD⊥PD,PD∩PH=P, PD⊂平面PAD,PH⊂平面PAD, 所以,CD⊥平面PAD. 又PA⊂平面PAD,所以,CD⊥PA. 17.由2c=4,得c=2,F1(-2,0),F2(2,0). 因此,∆PF1Q的周长=PF1+PF2+QF1+QF2=4a=12. 答:发酵池AD边长的范围是不小于15米,且不超过25米. ①b≥4时,S′(x)≥0,S(x)在[15,25]单调增,则x=15.即AB=AD=15米时,发酵馆的占地面积最小. 因为b1=1,b2=2,所以数列{bn}是以首项和公差均为1的等差数列,可得bn=n. 当a<0时,f′(x)>0,f(x)在(0,+∞)单调增. 设平面DEC的法向量为n=(x2,y2,z2),则 设二面角A-DE-C的平面角为α,则 23.当n=1时,设f(x)=ex-1-x,x∈(1,+∞),则f′(x)=ex-1-1>0,f(x)在(1,+∞)单调增. 所以f(x)>f(1)=0,即ex-1>x,即n=1时,原命题成立. 综上,原命题得证.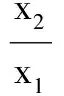
三、附加题(本大题有4小题,每小题10分,计40分.解答时应写出文字说明,证明过程或演算步骤)