一道椭圆定值问题的三个解题视角
2020-06-17 05:06渠怀莲
高中数学教与学 2020年9期
渠怀莲
(江苏省海门中学,226100)
圆锥曲线问题主要体现数学运算这一数学核心素养.数学运算主要包括理解运算对象、掌握运算法则,探究运算思路、选择运算方法,设计运算程序求得运算结果等.通过运算促进数学思维发展,形成规范化思考问题的品质.在圆锥曲线中我们经常会碰到定值问题,而定值问题的情况很多,包括定点与定直线、定向问题.定值问题泛指定长度、定角度、定面积、定乘积、定比例,以及定任意一个给定式子的值.本文通过一道椭圆中两定直线斜率之积为定值的问题求解,给出解决定值问题的三个视角,供读者参考.


视角1紧扣主题引入参数,设而不求或设而求之
解法1设直线l方程为x=λy+m,点E(x1,y1)、F(x2,y2),则



解法2设直线AE的方程为y=k1(x+2),与x2+2y2-4=0联立,得

评注这里采用了条件直译的方法,解法1引入直线的横截距式方程,采用设而不求策略,由韦达定理消去参数获解;解法2紧扣主题,引入直线的斜截式方程,设而求之,再借助三点共线找到其等量关系.两种解法都不容忽视.
视角2由共线向量定理引入参数,“曲线救国”


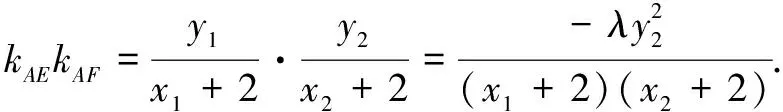
将x2的表达式代入,可得


评注解题是需要套路的,但又不能守旧,要善于打破常规解法.解法3用向量共线定理引入参数λ表示点的坐标,再用斜率公式化简得定值,与解法1异曲同工.
视角3巧用直线方程齐次化原则

解法4设直线EF的方程为λ(x+2)+μy=1,将点D(m, 0) 的坐标代入,可得λ(m+2)=1.

2y2-4μ(x+2)y+(1-4λ)(x+2)2=0.

猜你喜欢
中等数学(2022年6期)2022-08-29
新高考·高一数学(2022年3期)2022-04-28
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
新世纪智能(教师)(2021年2期)2021-11-05
中等数学(2021年4期)2021-08-14
中学生数理化·高一版(2021年5期)2021-07-21
校园英语·上旬(2019年6期)2019-10-09
电子制作(2018年10期)2018-08-04
电子制作(2018年12期)2018-08-01
中学生数理化·七年级数学人教版(2017年6期)2017-11-09

