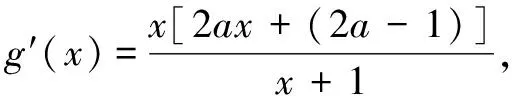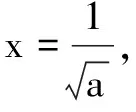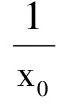聚焦难点 精准施策
——例谈一类含参不等式恒成立问题的难点突破
练育宏
(江苏省扬州市江都区教育局教研室,225202)
含参不等式恒成立问题一直是高中数学的重点问题,常与函数、导数 、不等式、方程等知识点相结合,渗透化归、数形结合、分类讨论等数学思想,综合性强且解法灵活. 很多学生面对此类问题有时感到力不从心,笔者归结为以下几个原因:一是方法的选择不当导致耗时费力;二是求解函数最值的“功力”不够深厚;三是不能合理利用化归等手段让问题简单化、熟悉化.下面借助于几道典型例题,对这类问题中所涉及的常用方法进行梳理,难点问题进行探究,以期抛砖引玉.
一、方法梳理
关于含参不等式恒成立问题,处理手法一般有以下三种分法.
(1)参变分离法,适用于参量与变量能够分离且含变量函数的最值可求型.一般形式为:f(x)>g(a)对x∈D恒成立⟺[f(x)]min>g(a)(x∈D);f(x) (2)整体函数法,适用于参变量分离比较困难或虽能够分离但求含变量的函数最值不易型.一般形式为:f(x,a)>0对x∈D恒成立⟺f(x,a)min>0(x∈D);f(x,a)<0对x∈D恒成立⟺f(x,a)max<0(x∈D)(a为参量). (3)数形结合法,适用于原不等式可化为f(x)>g(x) 或f(x) 例1设函数f(x)=ax3-3x+1(x∈R),若对于任意x∈(0,1]都有f(x)≥0成立,则实数a的范围是______. 分析该题入口宽,上述三种解法皆可实施,能通过一题多解揭示处理这类问题的常用方法. 解法1参变分离法 解法2整体函数法 综上,a≥4. 评注使用此法的关键是把握好分类标准的界定,本题分类的标准是导函数值的符号定与不定,不定时其零点是不是极值点. 解法3数形结合法 纵观上述三种方法,有两种涉及到函数最值,而求最值的难点主要表现在参量分离后的函数模型太复杂、整体构造函数求最值时分类讨论情况较多、分类的标准不知如何界定以及函数极值点存在但不可求等方面.下面归纳总结突破难点的策略,供大家参考. 策略1紧扣核心 以形助数 例2已知函数f(x)=ax2+ln(x+1),当x∈[0,+∞)时,不等式f(x)≤x恒成立,则实数a的取值范围______. 分析整体函数法是解决这类问题的通性通法,此题难点在分类讨论的标准界定上.在求导后一般抓住影响导函数符号的核心部分,紧扣核心函数值的符号或零点与区间的相对位置为分类的标准,以形助数化解讨论的难点. (1)当a=0时,u(x)=-x≤0,从而g′(x)≤0,g(x)在[0,+∞)单调减,g(x)≤g(0)=0,满足题意. (3)当a<0时,u(x)≤0,g′(x)≤0,g(x)在[0,+∞)单调减,得g(x)≤g(0)=0,满足题意. 综上,实数a的取值范围是(-∞,0]. 策略2特值代入,缩小范围 例3设函数f(x)=ax3-3x+1(x∈R),若对任意x∈[-1,1]都有f(x)≥0成立,求实数a的值. 分析本例为例1的变式,在原题的基础上弱化了条件,若采用前面的三种方法都需进行讨论,此时可尝试把区间的端点值代入预算,达到缩小参量取值范围的目的,简化讨论. 解依题意,在[-1,1]上f(x)min≥0.于是f(-1)≥0且f(1)≥0,解得2≤a≤4. 综上,a=4. 评注恒成立问题中用特值代入缩小参量取值范围,实质是利用必要性简化问题求解过程. 变式已知函数f(x)=ex-ax2-x-1,当x∈[0,+∞)时,f(x)≥0恒成立,求a的取值范围. 评注本题在考虑g′(x)的符号时,由x的端点值缩小参量取值范围,先找到问题成立的一个充分条件,再由补集思想验证其必要性,使问题完美获解. 策略3设而不求 整体代入 例4已知函数f(x)=aex-lnx-1(a>0),若f(x)≥0在(0,+∞)恒成立,求a的取值范围. 评注本题是极值点存在但不可求问题,突破难点的方法是对f′(x)的零点x0虚设而不求,再通过以形助数、整体代入等方法解决问题.






二、难点突破