挖掘隐性轨迹 妙解三角问题

何晓勤

(江苏省昆山市柏庐高级中学，215300)

在处理一些三角问题时,若能从轨迹思想入手,利用解析法处理,可达到事半功倍的效果.本文通过举例谈谈三角问题中的常见的隐性轨迹问题,供大家参考.

一、隐直线的应用

例1在∆ABC中,已知AB=2,AC2-BC2=6,则tanC的最大值是______.

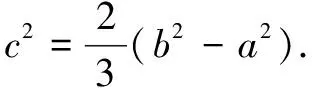
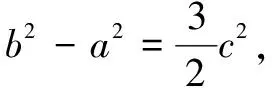
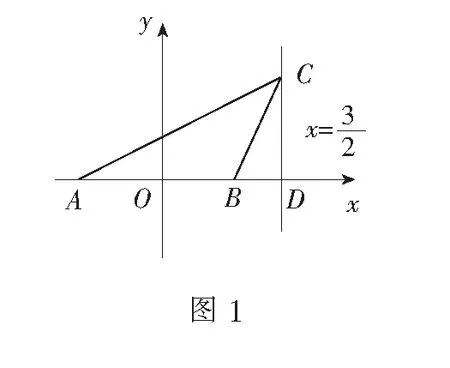
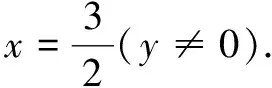
评注常规解法主要借助余弦定理寻求三边长之间的关系,再运用三角函数的性质及基本不等式求最值,对数学运算的要求较高;轨迹解法通过寻找点C的轨迹,再结合直角三角形与有向夹角公式、基本不等式求最值,优化了思维,简化了运算.一般地,在平面内,若A、B是两个定点,动点P满足PA2-PB2=λ(λ为常数),则点P的轨迹为与直线AB垂直的直线.

二、隐圆的应用

例2在∆ABC中,BC=4,sinC=2sinB,则当∆ABC的面积取得最大值时,BC边上的高为______.

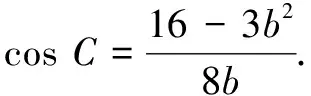
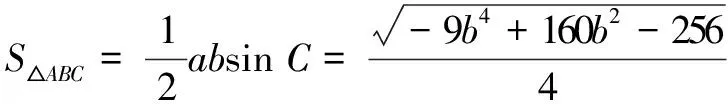
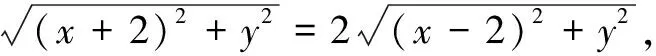
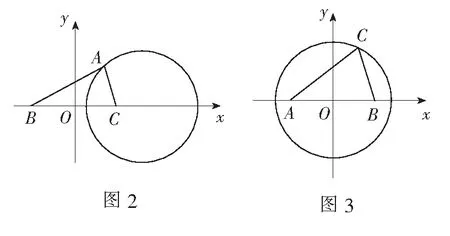
评注常规解法计算量较大,对数学运算素养要求较高;轨迹解法对思维要求较高,但能简化运算.一般地,在平面内到两定点A、B的距离之比为λ(λ>0且λ≠1)的动点P的轨迹是一个圆(该圆最先由古希腊数学家阿波罗尼斯发现,故称为阿波罗尼斯圆,简称为阿氏圆).

例3在∆ABC中,角A、B、C所对边分别为a、b、c,若a2+b2+2c2=8,则∆ABC的面积的最大值为______.

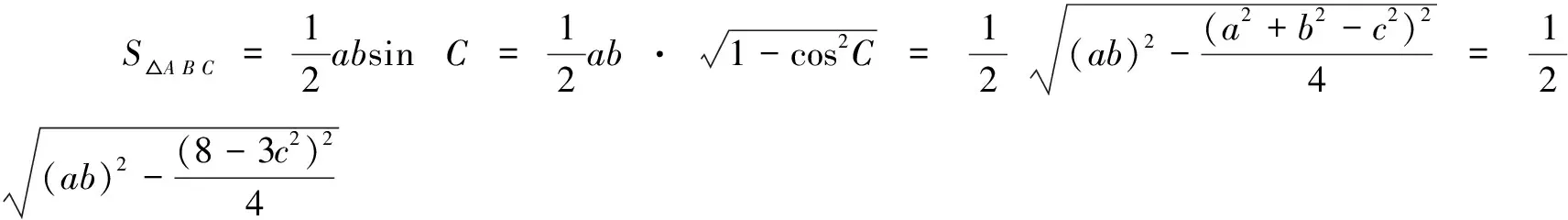
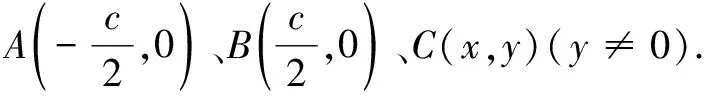
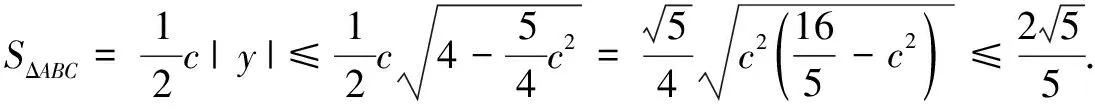
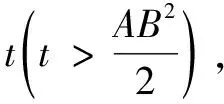
三、隐椭圆的应用

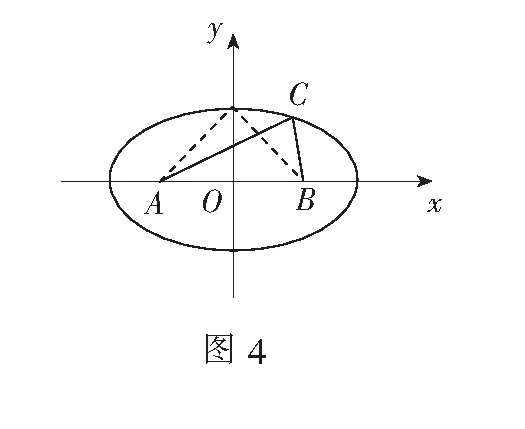
例4在∆ABC中,若AB=2,AC+BC=4,则∆ABC的面积S的取值范围为______.

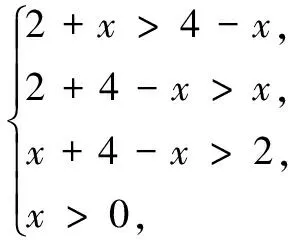
因∆ABC的周长为6,由海伦公式，可得

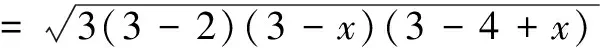
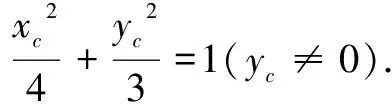
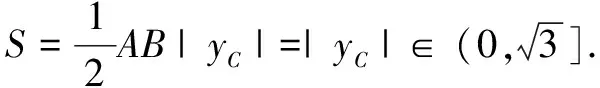
四、隐双曲线的应用

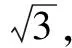
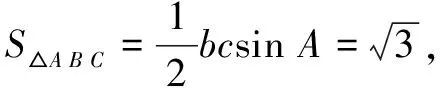
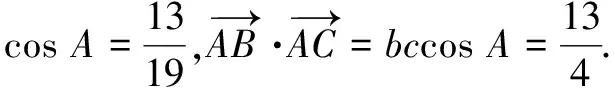
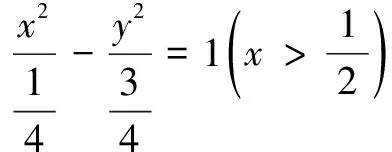
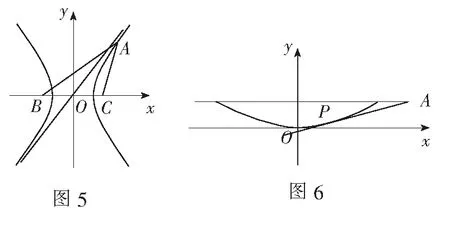
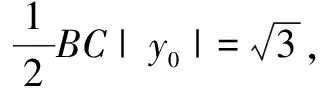
评注例4、例5从椭圆、双曲线的定义入手很容易探寻到动点的轨迹,再运用数形结合或利用向量坐标运算等相关知识可使问题轻松获解.

五、隐抛物线的应用

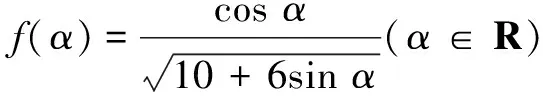
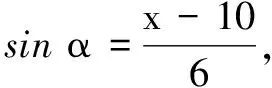
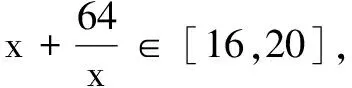
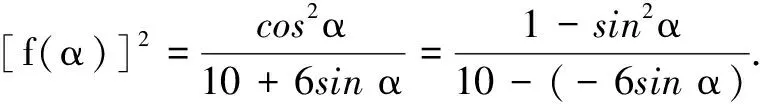
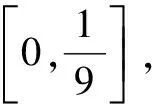
评注常规解法通过换元法,转化为常见函数(对勾函数)的值域问题处理;轨迹解法通过构造动点的轨迹(抛物线),运用数形结合思想能解决较较复杂的值域问题.

由上可见,有些三角问题看似与轨迹无关,但利用解析法挖掘隐性轨迹,能优化思维、简化运算、拓宽思维,有效培育数学运算和直观想象等数学核心素养.