强化思维训练 提升推理素养
——以数列教学为例
庞良绪
(上海市市西中学,200040)
《普通高中数学课程标准》(2017年版)指出:“逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养.主要包括两类:一类是从特殊到一般的推理,推理形式主要有归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.”它可以划分为三个水平:水平一能够在熟悉的数学内容中,识别归纳推理、类比推理、演绎推理;水平二能够在关联的情境中,发现并提出数学问题,用数学语言予以表达;水平三能够在综合的情境中,用数学的眼光找到合适的研究对象.
数学教学承载着培养学生思维能力的任务,“数学教学是思维的教学,数学活动是思维的活动”已成为广大一线教师的共识.因此,教学设计应围绕培养学生的思维能力,设计有思维价值的问题,让问题来撬动学生深度思考、探究,使课堂教学高效,在悄无声息中提升学生的数学素养.下面,笔者结合课堂教学实践,以数列为例,谈谈如何培养学生的逻辑推理素养.
一、寻找规律,实施归纳推理
归纳推理是根据一类事物的部分对象具有某种性质,推出这类事物的全部对象都具有这种性质的推理,其特点由部分到整体、由个别到一般.
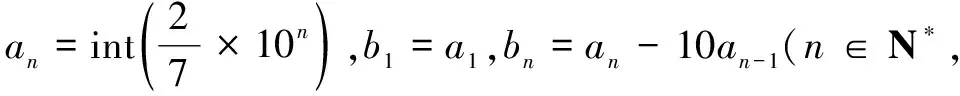
(A) 2 (B) 5 (C) 7 (D) 8
解计算可知b1=a1=2,b2=8,b3=5,b4=7,b5=1,b6=4,b7=2,…每6个一循环.又2 020=336×6+4,故b2 018=b4=7,选C.
评注通过计算初始项找规律,此情境学生较熟悉,属于水平一层次的归纳推理.
例2函数f(x)=sinωx(ω>0)的图象与其对称轴在y轴右侧的交点从左到右依次记为A1,A2,A3,…,An,…,在点列{An}中存在三个不同的点Ak、Al、Ap,使得∆AkAlAp是等腰直角三角形.将满足上述条件的ω值从小到大组成的数列记为{ωn},则ω2 019=______.
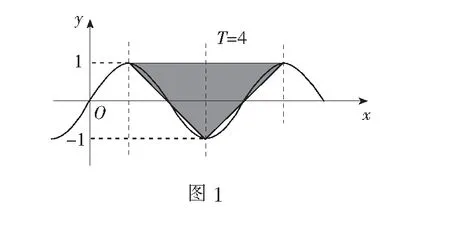
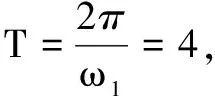
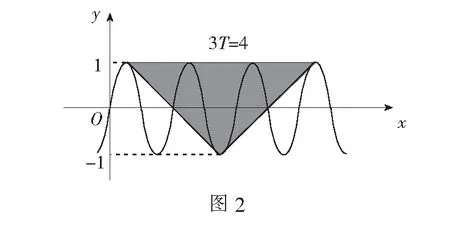
评注从特殊情况开始,求出ω1、ω2等,再到一般通项,此问题与三角函数关联,属于水平二层次的归纳推理.
例3已知定义在N*上的单调递增函数y=f(x),对任意n∈N*,都有f(n)∈N*,且f(f(n))=3n恒成立,则f(2 017)-f(1 999)=______.
解由题意f(f(1))=3,且f(n)∈N*.
若f(1)=1,则f(f(1))=f(1)=1,与已知矛盾;若f(1)=2,则f(f(1))=f(2)=3,符合题意;若f(1)≥3,则f(f(1))≥f(3),由单调性可知f(3)≥5,故f(f(1))≥5,与已知矛盾.所以,f(1)=2.
因此f(2)=f(f(1))=3,f(3)=f(f(2))=6,f(6)=f(f(3))=9,f(9)=f(f(6))=18.
再由单调性可知f(4)=7,f(5)=8,f(7)=f(f(4))=12,f(8)=f(f(5))=15.猜想:f(2·3k-1)=3k,f(3k)=2·3k(k∈N*).下面用数学归纳法证明.
当k=1时,结论显然成立.当k≥2时,假设f(2·3k-1)=3k,f(3k)=2·3k成立,则f(2·3k)=f(f(3k))=3k+1,f(3k+1)=f(f(2·3k))=2·3k+1.由归纳原理,猜想成立.
当n∈[3k-1,2·3k-1]时,f(3k-1)≤f(n)≤f(2·3k-1),即2·3k-1≤f(n)≤3k,而3k-2·3k-1=3k-1,所以f(n)=n+3k-1;当n∈[2·3k-1,3k]时,n-3k-1∈[3k-1,2·3k-1],则f(n-3k-1)=n-3k-1+3k-1=n,所以f(n)=f(f(n-3k-1))=3(n-3k-1)=3n-3k.
综上,可得
再由2·36<1 999<2 017<37,可得f(2017)-f(1 999)=3(2 017-1 999)=54.
评注此题的解决对思维水平要求较高,属于水平三层次的归纳推理.
二、运用迁移,实施类比推理
类比推理是根据两类事物之间具有某些类似性,推测一类事物具有另一类事物类似(或相同)的性质的推理,其特点是两类事物的相似性.
例4若{an}是等差数列,m、n、p是互不相等的正整数,有正确的结论:(m-n)ap+(n-p)am+(p-m)an=0.类比上述性质,相应地,若等比数列{bn},m、n、p是互不相等的正整数,有______.
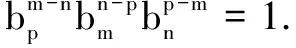
例5设{an}和{bn}均为无穷数列.
(1)若{an}和{bn}均为等比数列,试研究{an+bn}是否为等比数列?并请证明你的结论;若是等比数列,请写出其前n项和公式.
(2)请类比(1),针对等差数列提出相应的真命题(不必证明),并写出相应的等差数列的前n项和公式(用首项与公差表示).
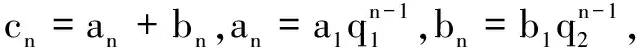
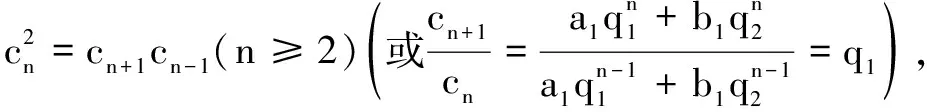
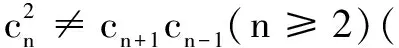
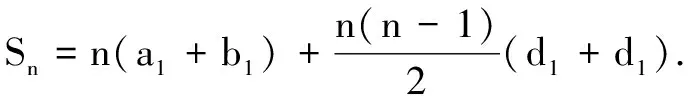
三、选择方法,实施演绎推理
演绎推理是从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理.简言之,演绎推理是由一般到特殊的推理,“三段论”是演绎推理的一般模式.
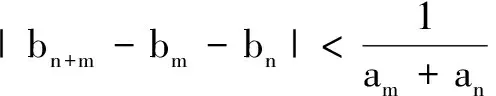
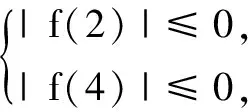
由此易得an=n(n∈N*).
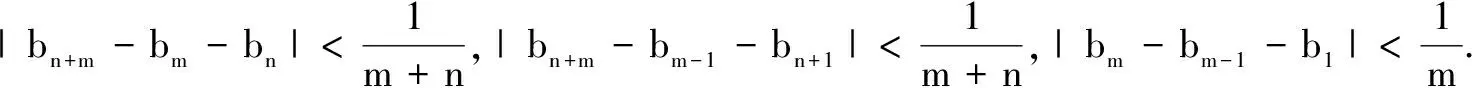
在上式中,令m→+∞,可得|bn+1-bn-b1|=0,即bn+1-bn=b1,所以{bn}是等差数列.得证.
例7给定无穷整数数列{xn}、{yn},若对任意n∈N*,都有|yn-xn|≤1,则称{yn}与{xn}“接近”.
(1)设整数数列{an}的前四项为1,2,4,8;{bn}是一个与{an}“接近”的整数数列.记集合M={x|x=bi,i=1,2,3,4},求M中元素的个数m.
(2)已知整数数列{an}是公差为d的等差数列.若存在与{an}“接近”的整数数列{bn},满足b2-b1,b3-b2,…,b201-b200中至少有100个为正数,求d的取值范围.
解(1)由题设条件,可得|b1-1|≤1,|b2-2|≤1,|b3-4|≤1,|b4-8|≤1,即0≤b1≤2,1≤b2≤3,3≤b3≤5,7≤b1≤9.
故bi(i=1,2,3,4)的取值存在b1=b2≠b3≠b4,或b1≠b2=b3≠b4,或b1≠b2≠b3≠b4三种情况, 从而集合M中元素的个数m=3或4.
(2)由{bn}与{an}“接近”,得|bn-an|≤1,即-1≤bn-an≤1,所以-1≤bn+1-an+1≤1,-1≤an-bn≤1.两式相加得-2≤bn+1-bn-d≤2,即d-2≤bn+1-bn≤d+2.
由于b2-b1,b3-b2,…,b201-b200中有正数,即必存在bn+1-bn>0,则必有d+2>0,得d>-2.
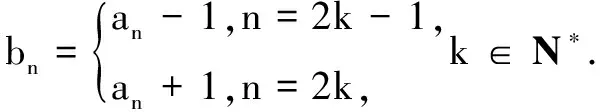
综上,所求d的取值范围是(-2,+∞).
——兼论数学证明中的推理

