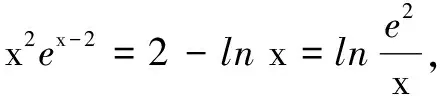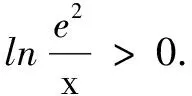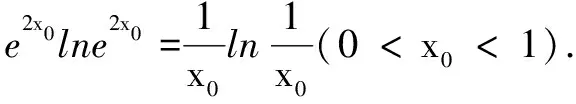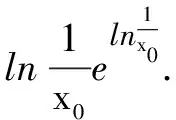用指数对数恒等式x=eln x简便解题*
甘志国
(北京市丰台区第二中学,100071)
以函数为背景的问题是中学数学常见的问题,其中有一类含指数函数与对数函数的综合题,按常规方法处理时过程比较繁琐,成为学生学习的难点问题.笔者经研究发现,其中有不少导数问题用恒等式x=eln x来求解很简洁.
一、求参数取值范围问题
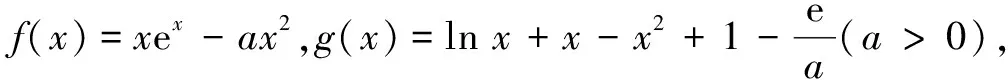
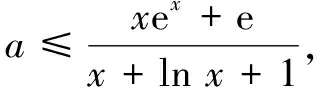
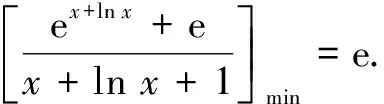
评注本题利用指数对数恒等式轻松得到最小值,避免了导数法求最值带来的繁琐计算,使解题过程分外简洁.
例2已知函数f(x)=ex-aln(ax-a)+a(a>0).若关于x的不等式f(x)>0恒成立,则实数a的取值范围为( )
(A) (0,e2] (B) (0,e2)
(C) [1,e2] (D) (1,e2)
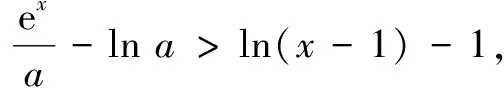
令g(t)=et+t(t∈R),则g(t)为单调增函数,题设不等式等价于x-lna>ln(x-1),即x-ln(x-1)>lna.
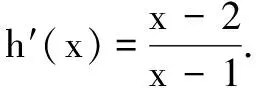
综上,选B.
评注本题无法分离参数,f′(x)的零点为虚零点,正面处理较困难.转换视角,对f(x)>0利用指数对数恒等式变形,方便了构造和利用辅助函数解决问题,降低了问题求解难度.
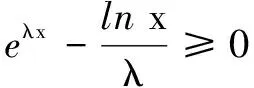
解当0 例4(2018年全国高考题) 已知函数f(x)=aex-lnx-1. (1)设x=2是f(x)的极值点,求a的值及f(x)的单调区间; 解(1)略. 由导数法易证明x≥ln(ex)=lnx+1成立,于是f(x)≥0成立.得证. 例5已知函数f(x)=ax-lnx. (1)讨论f(x)的单调性; f(x)≥2ax-xeax-1. 解(1)略. (2)f(x)≥2ax-xeax-1等价于ax-lnx≥2ax-xeax-1,即xeax-1-lnx≥ax,即xeax-1≥ax+lnx,亦即eax+ln x-1≥ax+lnx.可令t=ax+lnx,只要证明et-1≥t,即证et≥et(t∈R). 设函数h(t)=et-et(t∈R),则h′(t)=et-e,易见h(t)在(-∞,1)单调减,在(1,+∞)单调增,故h(t)≥h(1)=0,即et≥et(t∈R). 综上,f(x)≥2ax-xeax-1. 例6若y=x2ex-2+lnx-2=0,则e2-x+lnx=______. 故e2-x+lnx=eln x+lnx=x+lnx=2. 评注本题的题设条件为超越方程,无法直接求解.上述解法利用恒等式及函数的单调性挖掘隐含条件,使已知条件简化,揭示了问题本质,有效化解了直接求解的难度. 例7曲线y=xe2x-lnx-1的过坐标原点的切线的斜率为______. ① 下面用三种方法求切线的斜率. 评注本题第(2)问体现了恒等式的应用具有灵活性,需要我们根据问题特征灵活选择解决问题的角度.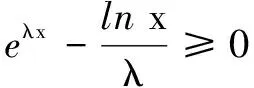
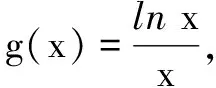
二、不等式证明问题
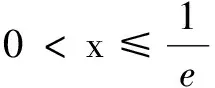
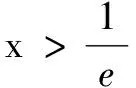
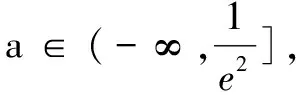
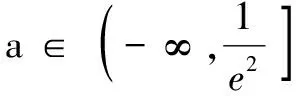
三、求值问题