浅谈抽象函数竞赛题的求解策略

方志平

(广东省惠州市第一中学, 516007)

抽象函数由于其外在形式高度抽象与内在性质隐而不露的特征，因而能较好地考查学生的抽象思维能力、逻辑推理能力,从而成为数学竞赛命题的热点素材.求解此类问题需要将抽象化与具体化结合起来，以化解函数抽象性带来的认知障碍.下面介绍求解的若干策略，供大家参考.

一、聚焦函数的基本性质

1.利用函数的单调性

例1(2013年全国高中数学联赛辽宁省预赛题)设函数f(x)是(0,+∞)内的单调函数,且对任意x∈(0,+∞)都有f[f(x)-log2x]=6.若x0是方程f(x)-f′(x)=4的一个解,且x0∈(a-1,a)(a∈N*),则a的值为( )

(A)1 (B)2 (C)3 (D)4

解由f(x)单调性和f[f(x)-log2x]=6知,存在唯一的实数c,使得f(x)-log2x=c,此式中再令x=c,得f(c)-log2c=c,结合f(c)=6,得log2c=6-c, 故c=4.

评注利用f(x)的单调性得到f(x)-log2x=c(常数)是求解本题的一个切入点.

例2(2017年全国高中数学联赛湖南省预赛题)设f(x) 是定义在(-∞,0)内的可导函数,其导函数为f′(x), 2f(x)+xf′(x)>x2, 则不等式(x+2 017)2f(x+2 017)-f(-1)>0 的解集为______.

解取函数F(x)=x2f(x),则F′ (x)=2xf(x)+x2f′(x)=x[2f(x)+xf′(x)](-1)2f(-1),即F(x+2 017)>F(-1), 于是x+2 017<-1, 得不等式的解集为(-∞，-2 018).

评注由条件不等式构造函数F(x)=x2f(x),再结合构造函数的结构形式，将所求不等式合适变形是求解的关键点.

2.运用函数的奇偶性

例3(2017年全国高中数学联赛新疆维吾尔自治区预赛题)已知函数f(x)是R上的单调减奇函数,若m、n满足

则5m-n的取值范围是______.

于是5m-n=2(m+n)+3(m-n)≥7,即5m-n的取值范围是[7,+∞).

3.挖掘函数的周期性

解取x=n,y=1, 得f(n)=f(n+1)+f(n-1);同理，有f(n+1)=f(n+2)+f(n),联立得f(n+2)=-f(n-1), 故f(n+3)=-f(n), 得f(n+6)=-f(n+3)=f(n),所以函数f(x)以6为周期.从而有f(2 019)=f(336×6+3)=f(3).

评注要求f(2 019)的值,在f(x)的解析式不易获得的前提下,通常利用函数f(x)的周期性解题.

二、妙用函数图象的对称性

例5(2018年全国高中数学联赛甘肃省预赛试题)已知函数f(x)=x3+sinx(x∈R),函数g(x)满足g(x)+g(2-x)=0(x∈R),若函数h(x)=f(x-1)-g(x)恰有2 019个零点,则所有这些零点之和为______．

解显然f(x)为奇函数,其图象关于原点对称,从而f(x-1)的图象关于点(1,0)对称.又由g(x)+g(2-x)=0可知g(x)的图象也关于点(1,0)对称,于是函数h(x)=f(x-1)-g(x)的图象也关于点(1,0)对称,可得题设中的2019个零点关于点(1,0)对称.

由h(1)=f(0)-g(1)=0,得x=1是函数h(x)的一个零点;其余2 018个零点首尾依次结合,两两关于点(1,0)对称,从而这2 018个零点之和为2 018, 故所有这些零点之和为2 019.

评注由f(x-1)和g(x)图象均是关于点(1,0)成中心对称,得函数h(x)图象是一个中心对称图形;又观察易知h(x)有一个特殊零点x=1,看清了这一点,问题轻松获解.

三、赋值法

解令x=y=0,易得f(0)=0.

令x=-1,y=1,得f(1)+f(-1)=6;又f(-1)f(1)≥9,故[6-f(1)]f(1)≥9,即[f(1)-3]2≤0,得f(1)=3.

例7(2015年全国高中数学联赛甘肃省预赛试题)设f(x)是定义在整数集上的函数,满足条件:①f(1)=1,f(2)=0;②f(x+y)=f(x)f(1-y)+f(1-x)f(y)对任意的x、y恒成立, 则f(2 015)=______.

解 令x=y=0,得f(0)=2f(0)f(1), 又f(1)=1, 则f(0)=0.再令y=1,得f(x+1)=f(1-x),得f(x)的图象关于x=1对称.

令y=-x,得f(0)=f(x)f(1+x)+f(1-x)f(-x), 即f(-x)=-f(x), 故f(x)为奇函数.结合f(x+1)=f(1-x),得f(x+1)=-f(x-1),即f(x+2)=-f(x),所以f(x+4)=f(x), 即f(x)以4为周期.

综上,f(2 015)=f(3)=-f(3)=-1.

四、借用函数模型

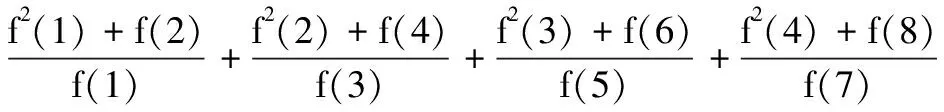
评注本题的函数方程很容易使人联想到指数函数模型,由于本题是填空题,用特殊法可使问题巧妙获解.

五、采用递推关系求解

评注在与整数、数列有关的问题或求值问题中,通过赋值得到递推关系式常常能够突破求解瓶颈.

总之，在求解抽象函数问题时,我们要善于观察题目的结构特征充分利用题目提供的信息 抓住关键点,找准切入点,分析问题与条件的关系,就可以拨开迷雾.本文给出的几种方法,仅仅是高中数学竞赛中求解抽象函数问题的冰山一角，这里略作介绍，以求抛砖引玉.