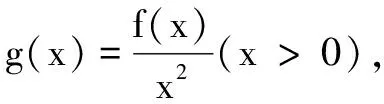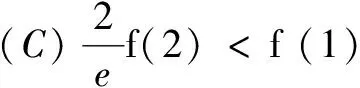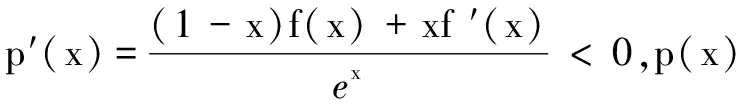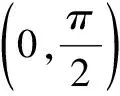精准构造函数 提高数学素养

赖佳佳

(广东省梅州市虎山中学高二(2)班，514299)

一、问题缘起

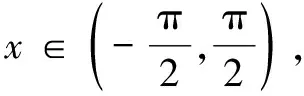
(A)① ③ (B)① ④

(C)② ③ (D)② ④

本题为广东省梅州市高二第一学期期末数学联考题,显然该题求解的关键是由题设不等式构造函数,再由函数的单调性比较大小得出结论.从评卷反馈的情况来看,该题的得分率较低.究其原因,问题源于构造函数使同学们犯了难.

二、解法分析

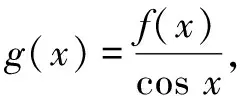
三、模型拓展

由上可见,要快速解答此类问题,需要同学们对基本初等函数的求导公式、四则运算及复合函数求导法则熟练掌握,并能通过组合变换对其延伸,才能准确地构造新函数,达到解题的目的.

纵观此类问题的解答,除了和差型函数引出的题设导数不等式问题比较容易求解外,使学生普遍感到困难的就是积商型函数及复合函数引出的相应问题.本文从源头出发列举几种常见模型,同学们只要通过类比推理进行拓展,就能精准构造新函数,探索得问题的求解轨迹.

模型1基于幂函数背景

对xf′(x)>-f(x),可构造新函数F1(x)=xf(x).拓展到一般,对xf′(x)>-nf(x),由[xnf(x)]′=xn-1[nf(x)+xf′(x)],可构造新函数G1(x)=xnf(x) (n∈Q*).

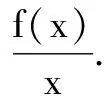
模型2基于指数函数背景

由f′(x)>-f(x),可构造新函数F3(x)=exf(x).拓展到一般,对f′(x)>-nf(x),由[en xf(x)]′=en x[nf(x)+f′(x)],可构造新函数G3(x)=en xf(x)(n∈Q*).

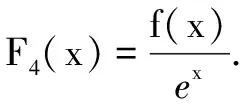
模型3基于幂函数指数函数混合背景

由p(x)=exxf(x)求导,可得p′(x)=ex[(x+1)f(x)+xf′(x)].由此拓展到一般,对xf′(x)>-(mx+n)f(x),由p′(x)=emxxn-1[(mx+n)f(x)+xf′(x)],可构造新函数p(x)=emxxnf(x) (m、n∈Q*).

模型4基于三角函数背景

由求导公式与法则,不难得到

[sinxf(x)]′=cosxf(x)+sinxf′(x)

=cosx[f(x)+tanxf′(x)]；

[cosxf(x)]′=-sinxf(x)+cosxf′(x)

=-cosx[tanxf(x)-f′(x)]；

由以上表达式,不难窥见相应命题的命制规律.

四、应用举例

例1已知定义在R上的函数f(x),其导函数为f′(x),且满足xf′(x)>2f(x),若a>b>0, 则下列不等式恒成立的是( )

(A)b2f(a)

(B)b2f(a)>a2f(b)

(C)a2f(a)

(D)a2f(a)>b2f(b)

例2已知定义在R上的函数f(x),其导函数f′(x)满足f′(x)0时,f(x)

解由模型2,令g(x)=e-xf(x),则g′(x)=e-x[f′(x)-f(x)]<0,g(x)在R上单调减;又g(0)=f(0)=1,故x>0时,有g(x)

例3已知定义在R上的函数f(x),导函数f′(x)满足xf′(x)+f(x)

解由条件知(1-x)f(x)+xf′(x)<0,按照模型3,可令m=-1,n=1,得p(x)=e-xxf(x).于是

(指导老师：江中伟)