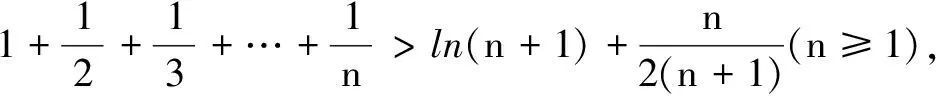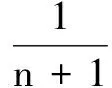核心素养之直观想象——例谈用定积分的几何意义巧解高考压轴题

郝安军

(陕西省安康市汉滨区江北高级中学，725000)

数学核心素养之直观想象,就是借助几何直观,利用图形理解和解决数学问题，通过建立数与形的联系,构建数学问题的直观模型.这也是培养一种数形结合思想,很多高考压轴题都可以运用数形结合的思想,使解答过程更加简洁、形象.例如，直观深刻理解定积分的定义,利用其几何意义,根据曲边梯形的面积和其相关梯形或矩形的面积大小,可以巧证不等式.本文通过几个实例,展示定积分的几何意义在高考压轴题中的巧妙应用.

(1)讨论f(x)的单调性;

解(1)略.

(2)由(1)知,f(x)存在两个极值点当且仅当a>2.

例2(2013年陕西高考题)已知函数f(x)=ex,x∈R.

(1) 若直线y=kx+1与f(x)反函数的图象相切, 求实数k的值;

(2) 设x>0, 讨论曲线y=f(x)与曲线y=mx2(m>0) 公共点的个数;

解(1)、(2) 略.

(3) 如图2,过图象上两点A(a,ea)、B(b,eb)分别作x轴的垂线AD、BC,D、C为垂足,因为y=ex是下凹函数,由图可知S曲边梯形ABCD

例3 (2014年陕西高考题)设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.

(1)设g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+,求gn(x)的表达式;

(2)若f(x)≥ag(x)恒成立,求实数a的取值范围;

(3)设n∈N+,比较g(1)+g(2)+…+g(n) 与n-f(n)的大小,并加以证明.

解(1)、(2)略.

评注本例更能体现直观想象建立直观模型进行证明的优势,这也是累和型不等式的一种证明方法.试题中代数式的和式结构被面积化,利用定积分定义可进行相关证明.

(1)用a表示出b、c;

(2)若f(x)>lnx在[1,+∞)上恒成立,求a的取值范围;

解(1)、(2)略.