特殊圆环面上曲边三角形内角的求解

林炯毅，夏丹阳，牟金平

特殊圆环面上曲边三角形内角的求解

林炯毅，夏丹阳，牟金平＊

（台州学院数学与信息工程学院，浙江临海317000）

将初等区域中的三角形映射到特殊的圆环面上，得到的像为圆环面上的曲边三条曲线。以圆环面上的曲边三角形为研究对象，以曲面上两方向的交角公式为工具，给出曲边三角形的内角的公式，并研究了特殊曲边三角形的内角规律。

圆环面；曲边三角形；内角

三角形是几何学中的重要图形，它拥有许多的几何性质［1］，被广泛运用于网络的定位、建筑物的加固和其他几何性质的研究［2，3］.目前，有许多关于平面曲边三角形的相关性质的研究.文献［4］给出了平面上曲边三角形内角的几个性质，比较了在不同条件下曲边三角形与二直角的关系.通常地，曲面上的曲边三角形不是平面图形，而它的性质是研究曲面上的曲边四边形、曲边五边形以及任意的曲边多边形的基本工具，即曲面上曲边多边形的性质可以通过曲边三角形来解决.而这方面的问题没有引起足够的重视.再则，曲边三角形的性质将为曲面上网络节点的定位提供必要的理论支持，而这方面的研究尚缺必要的理论基础.因此，研究曲面上的曲边三角形的内角公式和其性质是非常必要的.

1　预备知识

以向量函数为工具，文献［5］详细地介绍了初等区域、空间曲面等概念及性质.此外，文献［4］讨论了曲边三角形，这种三角形又称鲁洛三角形Reuleaux triangle，是指有一边或两边或三边为圆弧的三角形.在此基础上，本文将给出比文献［1］中更广的曲边三角形的概念.

定义1在xOz平面上取圆周y=0，（x-b）2+z2=a2（b＞a），并令其绕z轴旋转得圆环面，圆环面的参数方程是=｛（b+a cosφ）cosθ，（b+a cosφ）sinθ，sinφ｝（0≤φ＜2π，0≤θ＜2π）［5］.

为了便于计算，令圆环面中的a=1，b=2.

定义2设l1:y1=c1θ+d1、l2:y2=c2θ+d2、l3:y3=c3θ+d3为初等区域D上的三条直线，将这三条直线一一映射到三维空间的曲面上，得到3条空间曲线l1′、l2′、l3′，称由l1′、l2′、l3′三条曲线围成的曲面为曲面上的曲边三角形，记作△l1′l2′l3′，称其中三条曲线交点之间的弧线为边，交点为顶点.记、、为△l1′l2′l3′的顶点，并且=｛x（θ），y（θ），z（θ）｝，i=1，2，3.

特别地，如果△l1′l2′l3′是在圆环面上的，则称之为圆环面上的曲边三角形.在△l1′l2′l3′中，称由两曲边在交点处曲线切线的夹角为曲边三角形的内角.在△l1′l2′l3′中，如果有两内角相等，则称这个曲边三角形为曲边等腰三角形.

当定义2中的像曲面是平面时，定义2与定义1相同.因此，定义1中所指的曲边三角形是定义2中所提出的特殊形式.在下一节中，我们将讨论特殊圆环面（a=1，b=2）上曲边三角形的内角公式及其内角和.

2　主要结果

在这部分中，我们先给出圆环面上曲边三角形的参数方程，然后给出其交角公式，最后，本节将讨论曲边等腰三角形的性质.根据定义2，经过计算可得，圆环面上曲边三角形的参数方程为：

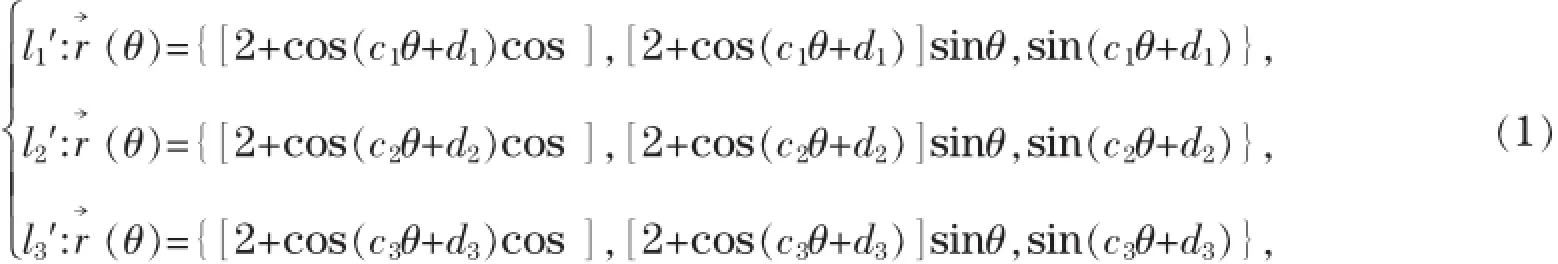
定理1设△l1′l2′l3′为圆环面上的曲边三角形，则曲边三角形的顶点向量为、、，其中

θ1、θ2、θ3分别代入到l1′、l2′、l3′中即得、、.

由定理1可得以下结果：

定理2设l1′、l2′、l3′为曲边三角形△l1′l2′l3′的三条边，则′（θ1）、′（θ1）、′（θ2）、′（θ2）、′（θ3）、′（θ3）分别为l1′、l2′、l3′在顶点δ1、δ2、δ3处沿曲边的切线方向，其中

证明：由定义2分别对三条曲线的向量函数求微商，得到

再将交点θ1分别代入′（θ）与′（θ），θ2分别代入′（θ）与′（θ），θ3分别代入′（θ）与′（θ），即得切线方向.

定理3设l1′l2′l3′为圆环面上的曲边三角形，γ1、γ2、γ3为曲边三角形的内角，则有

定理4设c1=1，c2=-1，c3=0，d1=π，d2=π，d2=0，则由初等区域为等腰直角三角形l1′l2′l3′，△l1′l2′l3′为曲边等腰三角形，其中△l1′l2′l3′是由l1∶y=x+π，l2∶y=x+π，l3∶y=x+π所围成.

证明：将c1=1，c2=-1，c3=0，d1=π，d2=π，d2=0代入到夹角公式中，得到cosθ1=-1，cosθ2=， cosθ3=由此算出θ=θ，所以此曲边三角形为曲边等腰三角形.

同时θ1=180°，θ2≈26.5651°，θ3≈26.5651°.

由于θ1+θ2+θ3＞180°，所以，当参数满足c1=1，c2=-1，c3=0，d1=π，d2=π，d2=0时，由初等区域中的等腰直角三角形映射而来的曲边等腰三角形的内角和大于180°.

证明：由定理4的证明方法即得.

3　结束语

本文讨论了特殊圆环面上曲边三角形的内角公式与曲边三角形的内角和.借助圆环面上曲边三角形的内角公式，我们可得出圆环面上曲边四边形、曲边五边形以及任意曲边多边形的内角公式.

［1］虞言林.三角形的内角和定理［J］.苏州教育学院学报，2004（21）:57-58.

［2］李亚莎，王泽忠.基于圆环坐标系的三维静电场曲边三角形边界元方法［J］.电工技术学报，2006，21（9）:122-126.

［3］张琦跃.一种曲边三角形区域中的三角形网格自动生成方法［J］.中国计量学院学报，1992，10（3）:17-84.

［4］韦静华.曲边三角形三内角和的探讨［J］.中学数学教学，1995，S1:144-145.

［5］梅向明，黄敬之.微分几何［M］.北京：高等教育出版社，2008：69-115.

（责任编辑：耿继祥）

The Interior Angles of Curved Triangle on the Special Torus

LIN Jiongyi，XIA Danyang，MOU Jinping＊
（Schoo l of Mathematics and Inform ation Engineefing，Taizhou University，Linhai 317000，China）

Mapping an elementary area of plan triangle to a special torus，w ill result in a curved triangle in torus（CTT）.Based on the formula of international angle of two directions，a formula of international angle of two directions is derived for CTT，and sum of angles of a CTT is discussed.

Torus；Curve triangle；Angle

10.13853/j.cnki.issn.1672-3708.2015.03.002

2015-03-12；

2015-05-21

台州学院培育基金（2013PY09）.

简介：牟金平（1974-），男，浙江黄岩人，讲师，博士，主要从事复杂系统的建模与分析的研究。