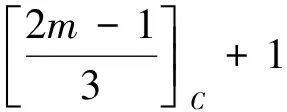一致超树谱半径的标尺定理
肖 鹏, 杜燕飞
(陕西科技大学 文理学院, 陕西 西安 710021)
0 引言
设H=(V,E)为包含n个顶点和m条边的超图,其中V=V(H)=(u1,u2,…,un)为n个顶点的顶点集,E=E(H)=(e1,e2,…,em)为m条边的边集.设u是超图H的一个顶点,H中包含顶点u的边数称为顶点u的度,记作d(u).用Δ(H)表示超图H的最大度.当d(u)=1时,称顶点u为悬挂点,否则称为非悬挂点.对1≤i≤n,记di=d(ui),称非增整数序列(d1,d2,…,dn)为超图H的度序列.设u1,u2,…,us+1为超图H中s+1个两两不同的顶点,e1,e2,…,es为超图H中s个两两不同的边,如果对1≤i≤s都有{ui,ui+1}⊆ei,则称点边交替序列P=(u1,e1,u2,e2,…,us,es,us+1)是一条连接顶点u1和us+1的路,其中s表示路P的长度.若对超图H中的任意两个顶点u和v,都存在一条连接u和v的路,则称H是连通的.如果超图H的每条边恰好包含k个顶点,则称H为k-一致超图,其中k≥2.当k=2时,2-一致超图是(普通)图.设H为包含n个顶点和m条边的连通k-一致超图,当n=(k-1)m+1时,称H是一棵k-一致超树.
2005年,文献[1,2]独立地提出了张量特征值的概念.此后,一致超图在张量表示下的特征值问题得到了广泛的关注[3,4].
设x=(x1,x2,…,xn)T是一个n维列向量,T是一个k≥2阶n维张量,用Txk-1表示一个n维列向量,它的第i个元素为
其中[n]={1,2,…,n}.
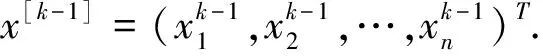
ρ(T)=max{|λ||Txk-1=λx[k-1],x≠0}.
设H为n个顶点的k-一致超图,H的邻接张量A(H)是一个k阶n维张量,张量A(H)的第(i1,i2,…,ik)元素为
A(H)i1,i2,…,ik=
设H为k-一致超图,称H邻接张量A(H)的谱半径为超图H的谱半径,记作ρ(H)=ρ(A(H)).
超图的谱半径是超图张量谱中一个重要的谱参数.近年来,各类超图依谱半径排序的问题被大量研究.文献[5-7]在给定顶点数的一致超树中,刻画了谱半径达到前八大值的一致超树.文献[8]在给定度序列的一致超树中,刻画了谱半径达到最大值的一致超树.受到上述工作的启发,本文将在给定边数和最大度的一致超树中,分别刻画使谱半径取到最大和最小值的一致超树.进一步,证明了一致超树谱半径的标尺定理,该定理给出了一个简单、高效比较一致超树谱半径的新工具.
1 预备知识
为了陈述主要结果,本节将给出一些预备知识.
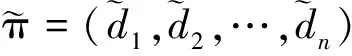
文献[8]定义了BFS-一致超树.设H=(V,E)为一棵根节点为v0的k-一致超树.如果存在顶点集V的一个良序关系“”满足下面的四个条件,则称这个良序为顶点集V的BFS-排序.
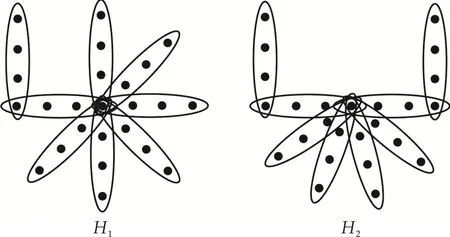
(a)若uv,则h(u) (b)若uv,则d(u)≥d(v); (c)设{u,u1}⊂e1∈E,{v,v1}⊂e2∈E, h(u)=h(u1)+1,h(v)=h(v1)+1,则u1v1; (d)对任意的边e={u1,u2,…,uk}∈E,假设u1u2…uk,则不存在顶点v使uivui+1,其中2≤i≤k-1. 对于一棵k-一致超树H,如果H的顶点集存在BFS-排序,则称H为BFS-一致超树. 设π为k-一致超树的度序列,用Tπ表示所有度序列为π的k-一致超树组成的集合. 引理1[8]设π为k-一致超树的度序列,则BFS-一致超树在Tπ中唯一取到谱半径的最大值. 设P=(u1,e1,u2,…,es,us+1)为k-一致超图H中连接顶点u1和us+1的路,如果d(u1)≥3,对任意的顶点u∈ei{ui,ui+1}(1≤i≤s)都有d(u)=2,d(ui)=2(2≤i≤s),则称P是一条长度为s的悬挂路. 设H为一个连通的k-一致超图,u和v是H的两个顶点,把两条长度为p和q的悬挂路分别挂在顶点u和v,得到超图H(u,v;p,q).当u=v时,H(u,v;p,q)简记为H(u;p,q). 引理3[9,10]设H为一棵k-一致超树,u和v是两个距离为d的顶点.当0≤d≤1,p≥q≥1时,ρ(H(u,v;p,q))>ρ(H(u,v;p+1,q-1)). 设G=(V,E)为2-一致超图,称k-一致超图H=(Vk,Ek)为G的k次幂超图,其中 Ek={e∪{ie,1,ie,2,…,ie,k-2}|e∈E}, 文献[11]给出了G与H谱半径之间的关系. 设H=(V,E)和H=(V′,E′)为两个k-一致超图.如果V⊆V′,E⊆E′,则称H是H′的子超图.若H是H′的子超图并且H≠H′,则称H是H′的真子超图. 引理5[3]设H和H′为两个连通的k-一致超图.若H是H′的真子超图,则ρ(H)<ρ(H′). 图1 k-一致超树 定理1设Δ≥2,则度序列为 的BFS-一致超树H在T(m,Δ,k)中唯一取到谱半径的最大值. 证毕. 证毕. 图2 k-一致超树 证毕. 证明:设H0在T(m,Δ,k)中唯一取到谱半径的最小值,且d(u0)=Δ.往证H0是由Δ条有唯一公共顶点的悬挂路组成的. 图3 k-一致超树 假设H0存在包含3个非悬挂点或度大于2顶点的边(除了包含顶点u0的边),并在这些边中选择一条与顶点u0距离最大的边,记作e0. 情形1:e0包含3个非悬挂点. 因为e0包含3个非悬挂点,所以H0是在某棵一致超树H的两个相邻顶点分别挂两条长度为p和q悬挂路P和Q得到的,其中p≥q≥1,即H0≅H(u,v;p,q).根据引理3,存在一棵超树H′≅H(u,v;p+q,0)使ρ(H0)>ρ(H′),矛盾.因此,H0不存在包含3个非悬挂点的边. 情形2:e0包含度大于2的顶点. 当e0至少包含1个度大于2的顶点u时,H0是在某棵一致超树的顶点u分别挂两条长度为p和q的悬挂路P和Q得到的,其中p≥q≥1.应用引理3,得到一棵超树H′≅H(u;p+q,0),使ρ(H0)>ρ(H′),矛盾. 证毕. 图4 3-一致超树 根据引理4有 容易验证, 证毕. 例2设H1和H2为两棵4-一致超树,如图5所示.其中Δ(H1)=7,Δ(H2)=6,k=4,m=8.根据定理5,易知ρ(H1)>ρ(H2).事实上,通过数值计算有ρ(H1)≈1.635 9,ρ(H2)≈1.593 6. 图5 4-一致超树H1和H2 例3设H3和H4为两棵4-一致超树,如图6所示.其中Δ(H3)=14,Δ(H4)=13,k=4,m=20.根据定理5,易知ρ(H3)>ρ(H4).事实上,通过数值计算有ρ(H3)≈1.950 7,ρ(H4)≈1.934 3. 图6 4-一致超树H3和H4
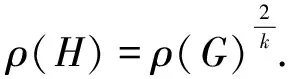
2 给定最大度时谱半径前两大的一致超树
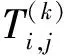
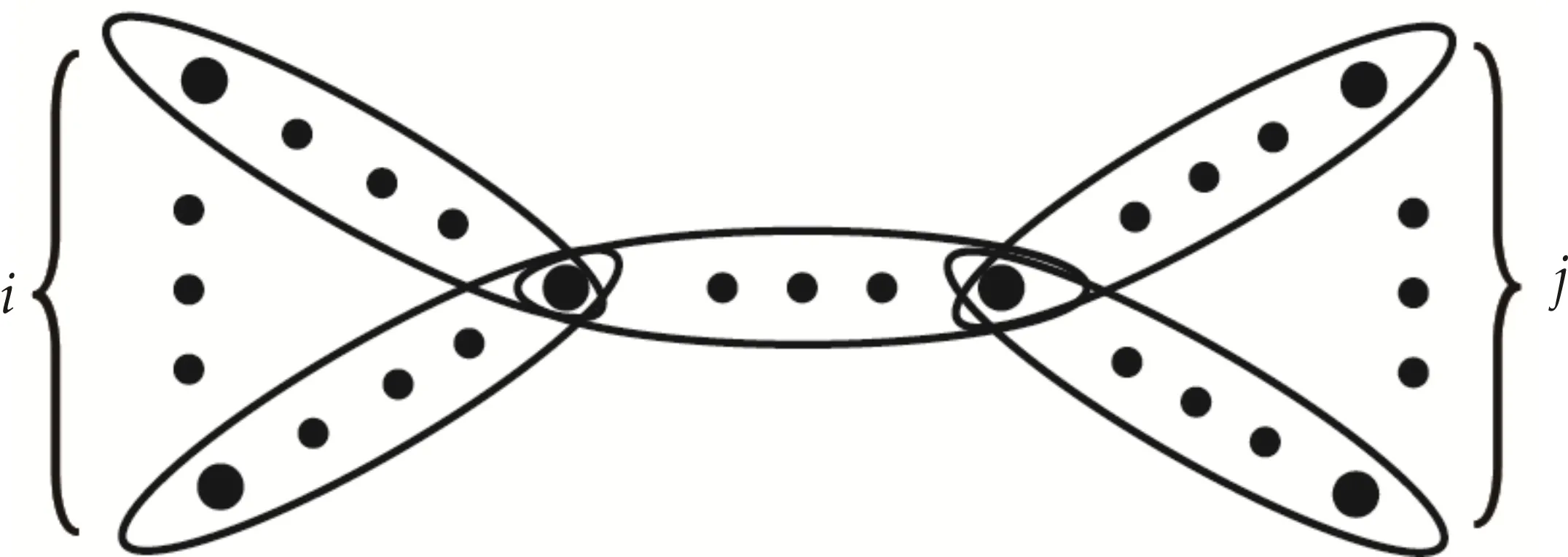
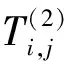
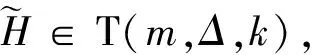
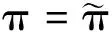
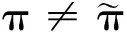

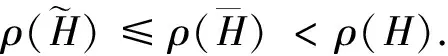


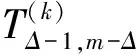
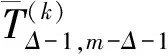
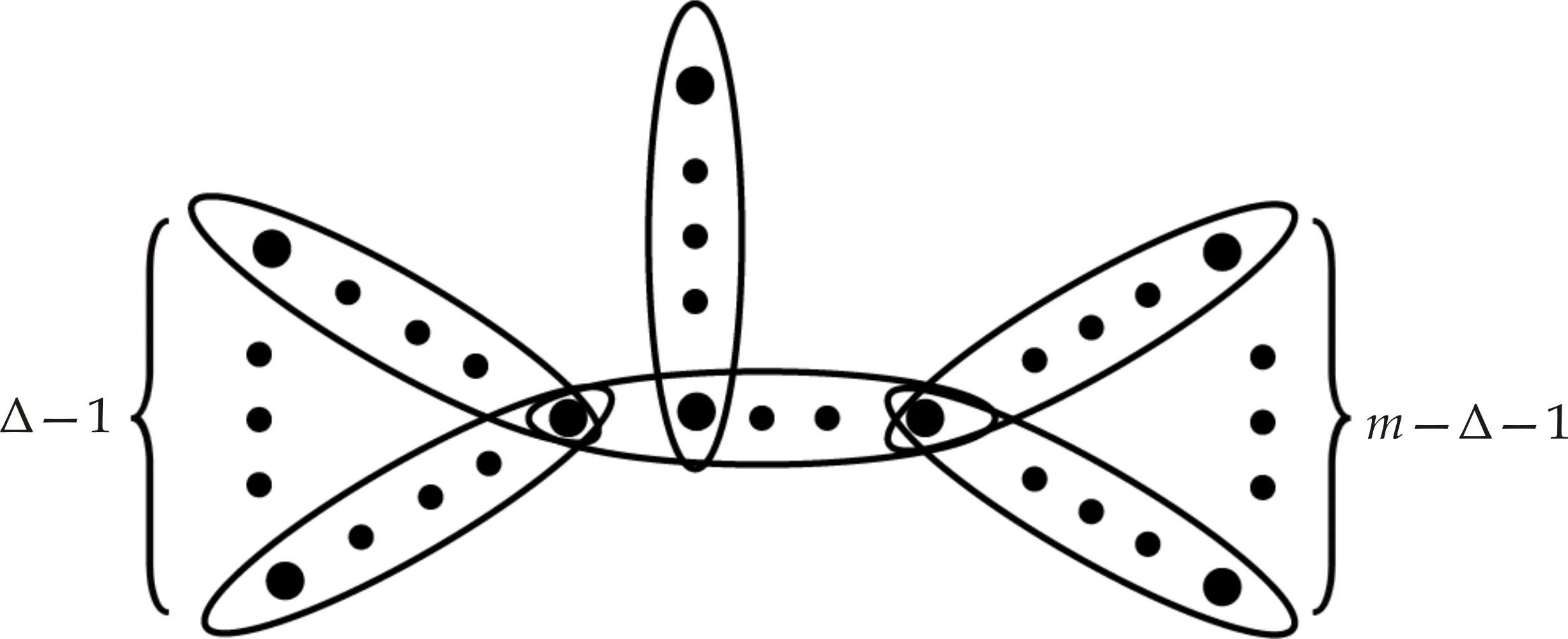
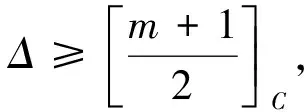

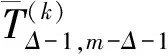

3 给定最大度时谱半径最小的一致超树



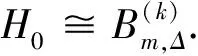


4 一致超树谱半径的标尺定理
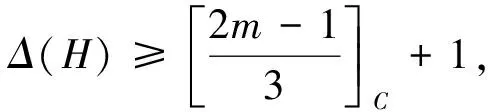


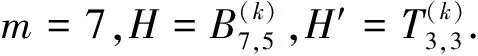
5 结论