图的Biharmonic指数的研究
郑学谦
(山西工程科技职业大学,山西 太原 030031)
0 引言
设图G为简单连通图,其中顶点集V={v1,v2,…,vn},边集E={e1,e2,…,em},最小度和最大度分别记为δ和Δ,顶点vi的度用di表示.若d1=d2=…=dn=d,则称图G为d-正则图.A=(aij)n×n表示图G的邻接矩阵,图G的度对角矩阵表示为D=diag{d1,d2,…,dn},图G的拉普拉斯矩阵表示为L=D-A,矩阵L的特征多项式|λI-L(G)|,称为图G的特征多项式,记作PG(λ),矩阵L的特征值称为图G的拉普拉斯特征值,记作0=λ1≤λ2≤…≤λn.
简单图G和H的并图G∪H[1]是指具有顶点集V(G)∪V(H),边集E(G)∪E(H)的简单图.简单图G和H的积图G×H[1]是指具有顶点集V(G)×V(H)的简单图,其中(u,v)与(u′,v′)相邻当且仅当u=u′且vv′∈E(H)或者v=v′且uu′∈E(G).
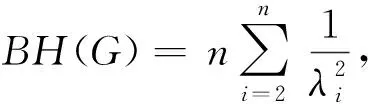
1 主要引理

等式成立当且仅当1≤i≤n,要么bi=qai,或者bi=pai.
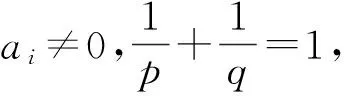
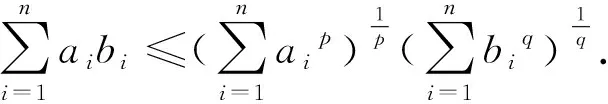
引理3[6]G是n个顶点m条边的简单连通图,最大度记为Δ,则λ2≥2m-(n-2)(Δ+1).
引理4[7]G是n个顶点m条边的简单连通图,最大度和最小度分别记为Δ,δ,则
引理5[6]G是n个顶点非完全图,λn=Δ+1,λn-1=λn-2=…=λ3,λ2=δ当且仅当G同构与下列图之一:2K1∨Kn-2,(K1∪Kn-2)∨K1,K1,n-1,K2∪(n-2)K1,Kn-1∪K1,K1,n-2∪K1.

引理7G是n个顶点m条边的d-正则简单连通图,则PL(G)(x)=(x-2d)m-nPG(x)
2 主要结论
定理1G是n个顶点m条边的简单连通图,
则BH(G)≤n[(q+p)(n-1)-pq(2m+M1(G))].

则BH(G)≤n[(q+p)(n-1)-pq(2m+M1(G))]


(n-1)2≤(2m+M1(G))(BH(G))

定理3G是n个顶点m条边的简单连通图,最大度和最小度分别记为Δ,δ,则

故定理成立.
定理4G同构与下列图之一:2K1∨Kn-2,(K1∪Kn-2)∨K1,K1,n-1,K2∪(n-2)K1,Kn-1∪K1,K1,n-2∪K1,则n
证明 由引理5得,当G同构与下列图之一:2K1∨Kn-2,(K1∪Kn-2)∨K1,K1,n-1,K2∪(n-2)K1,Kn-1∪K1,K1,n-2∪K1.λn=Δ+1,λn-1=λn-2=…=λ3,λ2=δ
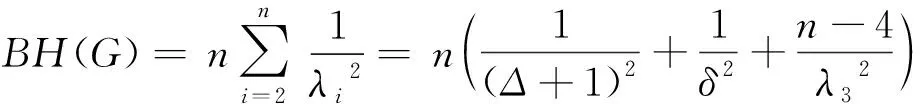

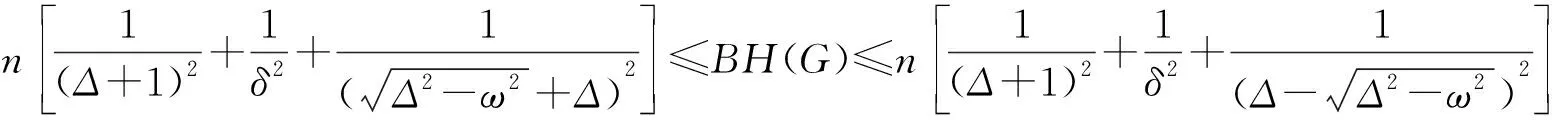

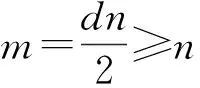
由引理7得PL(G)(x)=(x-2d)m-nPG(x)
则S(L(G))={2d,…,2d,λ1,…,λn},S(G)={λ1,…,λn}


