运用向量简证三角形内心坐标公式

云南省玉溪市第一中学(653100) 武增明

若∆ABC的内角A,B,C所对的边分别为a,b,c,顶点A(x1,y1),B(x2,y2),C(x3,y3),内心O(x0,y0),则

为了便于广泛交流,把此结论称之为三角形内切圆圆心坐标公式,即三角形内心坐标公式.

三角形内心坐标公式,文字表述简洁,符号表述漂亮,结构优美,十分有趣,让人赏心悦目,享受到数学之美,感受到数学的魅力,且有着广泛的用途.由此引起笔者极大的探究兴趣与热情,笔者查阅了大量的资料,没有找到三角形内心坐标公式的证明记录.笔者反复思考,反复推算,调整思维,受文[2]的启示,笔者想到运用向量探究三角形内心坐标公式的简证,获得成功,形成此文,与大家分享、共赏.

简证1因为点O是∆ABC的内心,连接AO并延长交边BC于点D,连接BO,CO,如图1,则由三角形内角平分线性质定理,有所以于是

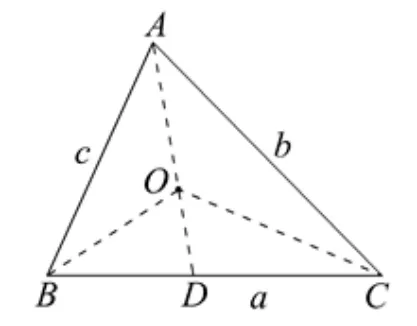
图1

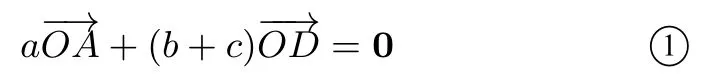
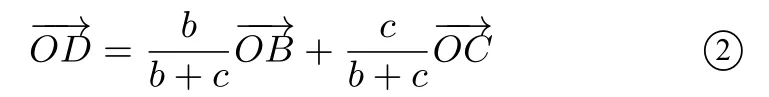
②代入①,得

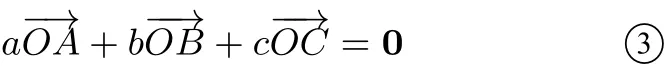
因为A(x1,y1),B(x2,y2),C(x3,y3),O(x0,y0),所以由③,得a(x1−x0,y1−y0)+b(x2−x0,y2−y0)+c(x3−x0,y3−y0)=0 即

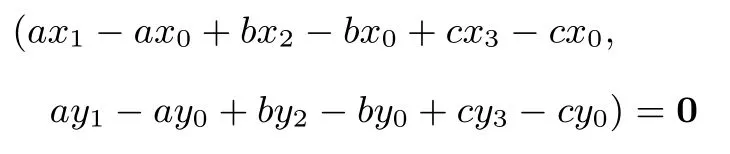
所以ax1+bx2+cx3−(a+b+c)x0=0,ay1+by2+cy3−(a+b+c)y0=0 故

简证2连接AO,作OD ⊥AC交边AC于点D,如图2.设∆ABC的内切圆半径为r,则OD=r.因为AO平分∠BAC,所以可设−→AO=,所以

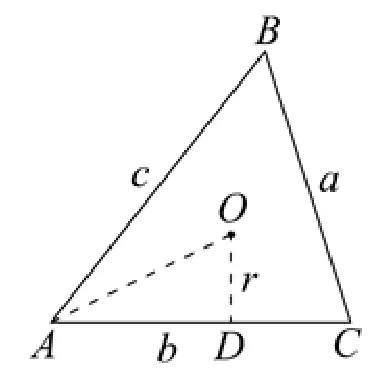
图2

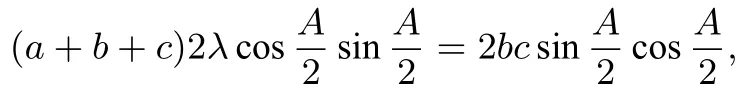
因为A(x1,y1),B(x2,y2),C(x3,y3),O(x0,y0),所以

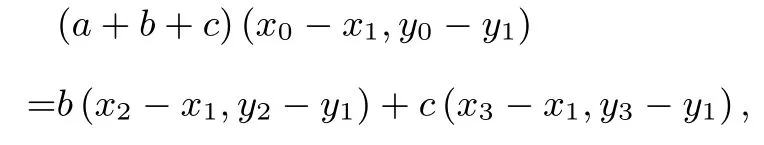
故而(a+b+c)(x0−x1)=b(x2−x1)+c(x3−x1)

(a+b+c)(y0−y1)=b(y2−y1)+c(y3−y1)

说明同理,可得