寻找隐直线解决非直线问题*——基于数学核心素养的试题研究

广东省兴宁市第一中学(514500) 肖建平

直线是非常直观的,借助函数图像的切线(分界线)解题,具有非常强的视觉感受.切线是曲线割线的极限位置,它反映了曲线的局部的几何性质.如果我们能够寻找到函数隐藏的直线(切线或者分界线)进行解题,往往可以简化运算,为解题带来极大的方便.本文基于数学核心素养的视角,结合GeoGebra 软件画图,来研究近年高考(模拟)题,探讨寻找隐直线(切线或者分界线)解决非直线问题.

使用GeoGebra 软件画图,可以直观的看出函数图像的弯曲方向,从而涉及到函数的凹凸性.曲线上任意两点间的弧段总在这两点连线的下(上)方的曲线称为凸(凹)的,相应的函数称为凸(凹)函数.

定义[1]设f为定义在区间I上的函数,若对I上的任意两点x1,x2和任意实数λ ∈(0,1)总有f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2),则称f为I上的凸函数.反之,如果有f(λx1+(1−λ)x2)≥λf(x1)+(1−λ)f(x2),则称f为I上凹函数.

定理[1]设称f为I上的可导函数,则下述论断互相等价:

1°f为I上的凸函数；

2°f′为I上的增函数；

3°对I上的任意两点x1,x2,有f(x2)≥ f(x1)+f′(x1)(x2−x1).

注1论断3°的几何意义是:当x ∈I时,曲线y=f(x)总是在它的任一切线的上方.

注2对于凹函数f,则f′为I上的减函数,曲线y=f(x)总是在它的任一切线的下方.

注3定理的证明过程请查阅参考文献[1].

结合凸(凹)函数的定义及定理,可以使我们对函数的认识更加精确.

例1(2019年高考全国卷I 文科第20 题)已知函数f(x)=2 sinx −xcosx −x,f′(x)为f(x)的导数.

(1)证明:f′(x)在区间(0,π)存在唯一零点;

(2)若x ∈[0,π]时,f(x)≥ax,求a的取值范围.

解(1)因为f′(x)=cosx+xsinx−1,f′′(x)=xcosx.当时,f′′(x)>0,当时,f′′(x)<0,所以f′(x)在单调递增,在单调递减.又f′(0)= 0,所以f′(x)在(0,π)存在唯一零点.

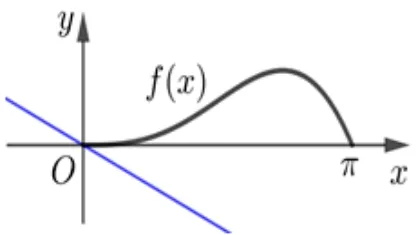
图1

(2)由(1)知,f′(x)在(0,π)存在唯一零点,设为x0,且当x ∈(0,x0)时,f′(x)>0,f(x)在(0,x0)单调递增;当x ∈(x0,π)时,f′(x)<0,f(x)在(x0,π)单调递减,又因为f(0)= 0,f(π)= 0,所以x ∈[0,π]时,f(x)min= 0,所以f(x)≥0 成立,由f(x)的图像可知,f(x)的图像都在直线y=0 的上方.直线y=ax是过原点O(0,0)的直线系,当直线y= 0 绕原点O(0,0)从水平方向顺时针旋转至与x轴垂直时满足题意,所以a的取值范围是(−∞,0].

评注本题是不等式恒成立问题,通过研究过定点的直线y=ax与函数f(x)=2 sinx −xcosx −x图像的位置关系,进而应用运动的数学思想结合图形直观想象,求解参数a的取值范围.

例2(2017年高考全国卷II 文科第21 题)设函数f(x)=(1−x2)·ex.

(1)讨论f(x)的单调性;

(2)当x≥0 时,f(x)≤ax+1,求a的取值范围.

解(1)f(x)在单调递减,在单调递增,解答过程略.

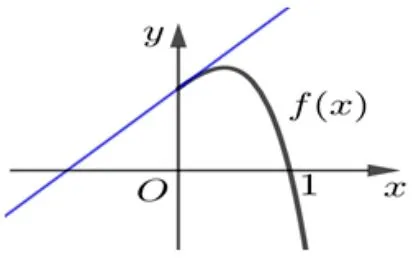
图2

(2)因为f(x)= (1−x2)· ex,所以f′(x)= (1−2x −x2)·ex,当x ∈(0,+∞)时,f′′(x)=−ex(x2+4x+1)<0,f′(x)在(0,+∞)单调递减,由定理得f(x)为(0,+∞)上的凹函数.因为f′(0)= 1,f(0)= 1,所以f(x)在点(0,1)处的切线方程是y=x+1,由f(x)≤ax+1 等价于凹函数f(x)的图像都在切线y=x+1 的下方.直线y=ax+1 是过定点(0,1)的直线系,当直线y=x+1 绕定点(0,1)逆时针旋转至垂直时满足题意,所以a的取值范围是[1,+∞).

评注本题是不等式恒成立问题,看作是过定点的直线y=ax+1 与函数f(x)=(1−x2)·ex图像的位置关系;再利用导数的几何意义,应用运动的数学思想结合图形直观想象,转化为过定点的直线的斜率与切线的斜率的大小关系求解参数a的取值范围.

例3(2016年高考全国卷II 文科第20 题)已知函数f(x)=(x+1)lnx −a(x −1).

(1)当a=4 时,求曲线y=f(x)在(1,f(1))处的切线方程;

(2)若当x ∈(1,+∞)时,f(x)>0,求a的取值范围.

解(1)曲线y=f(x)在(1,f(1))处的切线方程是2x+y −2=0,解答过程略.

(2)因为当x ∈(1,+∞)时,f(x)>0,即(x+1)lnx −a(x−1)>0,即(x+1)lnx>a(x−1),记g(x)=(x+1)lnx,x∈[1,+∞),所以g(x)>a(x −1).

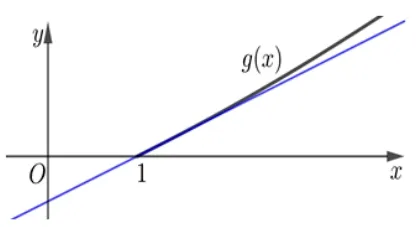
图3

评注本题与例1、例2 有所不同,乍看与直线没有关系,但是通过适当的恒等变形,部分分离,化为过定点的直线y=a(x −1)与函数g(x)=(x+1)lnx图像的位置关系;再应用运动的数学思想结合图形直观想象,转化为过定点的直线的斜率与切线的斜率的大小关系求解参数a的取值范围.

例4(2015年高考山东卷理科第21 题)设函数f(x)=ln(x+1)+a(x2−x),其中a ∈R.

几人嬉笑一番，赵仙童告辞。接下来，赵仙童走访了市文联、市作协、市戏剧家协会、中青旅行社，到家已错过了午饭时间，砖子正在啃脆脆的快餐面。午饭前，砖子打过赵仙童手机，赵仙童没接，莫名其妙地关机了。

(1)讨论函数f(x)极值点的个数,并说明理由;

(2)若∀x>0,f(x)≥0 成立,求a的取值范围.

解(1)当a <0 时,函数f(x)有一个极值点; 当时,函数f(x)无极值点; 当时,有两个极值点;解答过程略.

(2)因为∀x>0,f(x)=ln(x+1)+a(x2−x)≥0 成立,所以a(x2−x)≥−ln(x+1),所以由于ex≥x+1,所以x≥ln(x+1),当且仅当x=0 时等号成立.因为x>0,所以所以则a(x−1)>−1,所以f(x)≥0 等价于a(x −1)> −1,记g(x)=−1,(x >0),直线l:y=x −1,所以直线l过点(1,0)和(−1,0),由函数g(x)的图像是平行于x轴的一条射线(不含端点)和直线l的图像得g(x)的图像都在直线y=a(x −1)的下方.直线y=a(x −1)是过定点(1,0)的直线系,当直线l:y=x −1绕定点(1,0)顺时针旋转至x轴时满足题意,故0 ≤a≤1,所以a的取值范围是[0,1].

图4

评注本题初看与直线没有关系,但是通过适当的恒等变形,分离出直线,利用常见的不等式ex≥x+1 进行放缩,变为过定点的直线y=a(x −1)与函数g(x)=−1,(x>0)图像的位置关系;再应用运动的数学思想结合图形直观想象,转化为过定点的直线的斜率的取值范围来求解参数a的取值范围.

例5若恒成立,求实数a的取值范围.

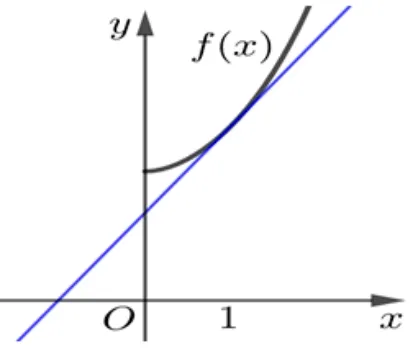
图5

直线y=a(x+1)是过定点(−1,0)的直线系,因为所以f(x)在(0,+∞)单调递增,设f(x)的过点(−1,0)切线l与y=f(x)的切点为,则切线l的斜率

又因为

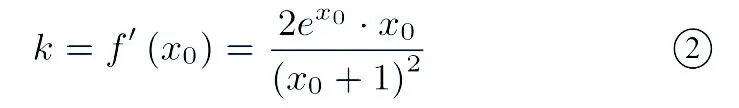
评注本题是指数与对数混杂的函数不等式,通过利用对数平均不等式进行放缩就会豁然开朗,从而转化为过定点的直线y=a(x+1)与函数图像的位置关系;再应用运动的数学思想结合图形直观想象,转化为过定点的直线的斜率的取值范围来求解参数a的取值范围.

例6(2020 届高三广东六校二联)已知函数f(x)=lnx+x+1,g(x)=x2+2x.

(1)求函数y=f(x)−g(x)的极值;

(2)若实数m为整数,且对任意的x >0 时,都有f(x)−mg(x)≤0 恒成立,求实数m的最小值.

解(1)极大值为无极小值,解答过程略.

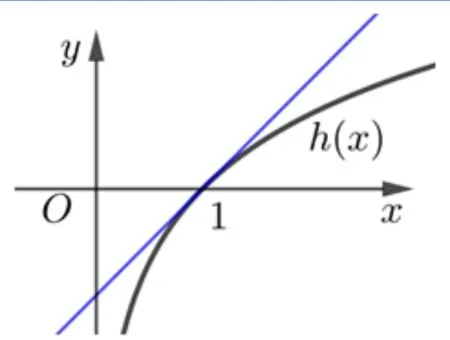
图6

(2)因为∀x >0 时,f(x)−mg(x)≤ 0 恒成立,所以设函数h(x)= lnx,函数h(x)=lnx在点(1,0)处的切线为y=x −1,因为在(0,+∞)上单调递减,由定理得h(x)是(0,+∞)上的凹函数,则凹函数h(x)的图像总是在切线y=x −1 的下方,所以lnx ≤x −1,当且仅当x= 1 时等号成立,所以当且仅当x= 1 时等号成立,所以当时,有因为当x >0 时,是减函数,所以x ≥1,所以整数m的最小值为1.

评注本题灵活运用常见的不等式lnx≤x −1 进行放缩,大大简化了运算,实现问题的快速解决.

通过上面的例题可知,导数压轴题能够分离出直线方程或者能寻找出隐藏的切线(分界线)的,可以根据图形直观想象,再结合运动与静止的相对观念,求出参数的取值范围或最小值.当然,我们也要夯实基础,熟练掌握常见的不等式,进行适当的放缩可以简化运算.同时,在直观想象核心数学素养的形成过程中,能够进一步发展几何直观和空间想象能力,增强运用图形和空间想象思考问题的意识,提升数形结合的能力,感悟事物的本质,培养创新思维.