再谈导数中的双变量问题

湖南省怀化市铁路第一中学(418000) 高 用

在近几年各地高考及模拟试题中,导函数压轴题频繁出现双变量的问题,此类题型因含有两个变量,思维量大,解题方法灵活,对学生的数学抽象、数学运算等核心素养提出了很高要求.为此,本文通过具体例题的求解谈谈求解导数中双变量问题的解题思想和几种有效方法,希望能对广大教师同行的教学有益.

1.等量消元,去二为一

二元变量问题难的主要原因就在于所含两个变量同时变化难以控制,所以将双变量转化为单变量势在必行.消元,通常是利用变量所满足的等量关系进行代换,消去其中一个变量,留下唯一变量,即去二为一,使之成为一元变量问题求解.

例1(2018年高考全国Ⅰ卷理科第21 题)已知函数

(1)讨论函数f(x)的单调性;

(2)若函数f(x)存在两个极值点x1,x2,证明:

分析x1,x2为函数f(x)的极值点,即x1,x2是方程f′(x)= 0 的根,则方程的根与系数满足等量关系,于是可以试着通过这一条件寻找x1与x2的等量关系,进而利用此等量消元,即而转化为一元变量问题求解.

解析(1)f(x)的定义域为

(i)若a≤2,则f′(x)≤0,所以f(x)在(0,+∞)单调递减.

(ii)若a >2,令f′(x)<0 得,或所以f(x)在单调递减,在单调递增.

(2)由(1)知,当且仅当a>2 时,f(x)存在两个极值点.

由于f(x)的两个极值点x1,x2满足x2−ax+1 = 0,所以x1+x2=a,x1x2= 1,不妨设x1< x2,则x2>1.即

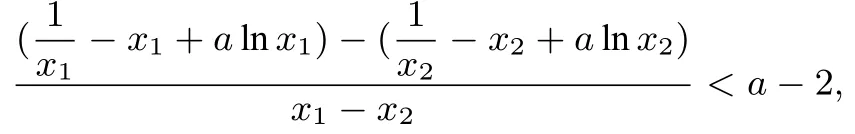
评注一般题目明确给出或者隐含关于两个变量的等量关系,则可以通过这个等量关系,实现两变量的相互代换,是能够消元处理这种问题的明显信号,而像例1 一样给出根与系数的关系的题目是利用消元求解的常见题型.

2.整体换元,合二为一

如果两个变量间不存在等量关系,但可以通过适当地代数变形将两个变量化为某种结构的整体,常见的如x1−x2,就可以利用换元实现双变量合二为一的目的,这也是把双变量转化为单变量的一种有效手段.

例2已知函数f(x)=lnx,g(x)=ax −a,a ∈R.

(1)若直线y=g(x)是曲线y=f(x)的一条切线,求a的值;

(2)若P(x1,y1),Q(x2,y2)是曲线y=h(x)=f(x)−g(x)上的两个不同的点,证明:

分析此题条件没有给出x1,x2的等量关系,则无法直接消元,可以先尝试将要证的不等式进行等价变形,不难发现两个变量x1,x2能够化为的整体形式,从而实现整体换元,转化为一元问题求解.

解(1)a=1.

(2)的证法1h(x)=f(x)−g(x)= lnx −ax+a,则

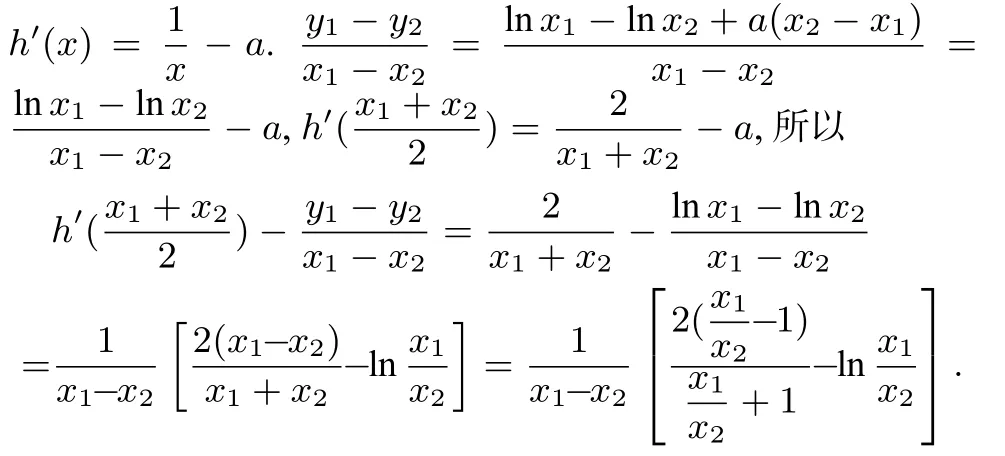
不妨设0< x2< x1,则令则

评注判断是否能够把两个变量化为的形式进行整体换元,代数式中出现lnx是一个标志.另外,除lnx之外的部分要能够整理成关于x1,x2的齐次分式,如例2 中,通过提公因式得从而变形得到关于x1,x2的二次齐次分式

(2)的证法2不妨设0< x2< x1,令则x1=tx2,t>1,所以

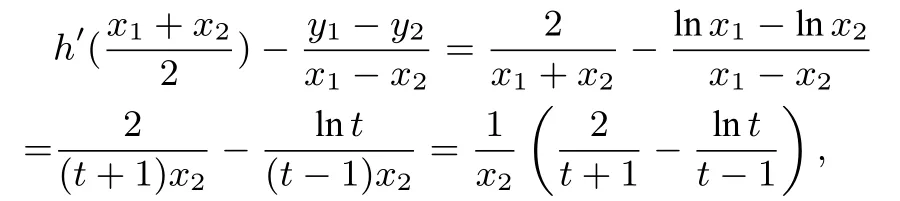
例3已知函数f(x)=ex,x ∈R.设a < b,比较的大小,并说明理由.

分析作差比较两式的大小,由于题目没给两变量a,b的等量关系的条件,于是尝试整体换元.因为式子中出现了ex,作差之后不能像例2 一样出现两变量的商但可以通过提公因式,使得指数出现两变量的差b −a,所以试图将两个变量整理成b −a的形式实现整体换元.

解法1设

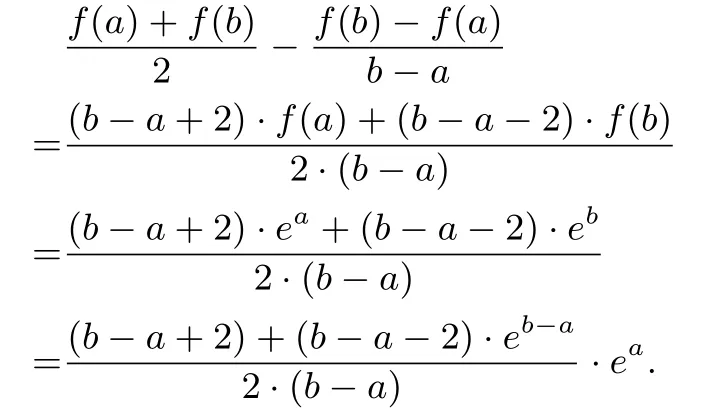
设x=b −a,并令g(x)=x+2+(x −2)·ex,x>0,则g′(x)=1+(x −1)·ex.

因为g′′(x)= (1+x −1)·ex=x·ex>0,所以g′(x)在(0,+∞)上单调递增,又g′(0)= 0,因此g′(x)>0,所以g(x)在(0,+∞)上单调递增,而g(0)= 0,所以在(0,+∞)上g(x)>0,即g(x)=x+2 +(x −2)· ex>0.所以故当a < b时,

事实上,此题也可以将不等式等价代数变形,化为对数形式,于是就可以把两变量整理成商的形式实现整体换元了.

解法2要证明亦即证明

令x=eb,y=ea(x > y >0),不等式等价于变形得:即

评注整体换元求解双变量问题时,一般地,若代数式中出现lnx,则将两个变量化为商的形式整体换元,如果出现的是ex,就将两个变量化为差的形式整体换元.当然,通过适当的代数变形可以实现指数与对数的互换.

3.对称分离,化二为一

例4已知−ax+(a −1)lnx,a >1.证明:若a <5,则对任意x1,x2∈(0,+∞),x12,有

分析不难发现要证的不等式中两个变量x1,x2在结构上是对称的,而且容易分离,于是将两个变量分离之后便可以得到g(x1)> g(x2)的形式,结合题意,对任意x1,x2∈(0,+∞),g(x1)> g(x2)成立,从而转化为g(x)的单调性来求解.

解析不妨设x1> x2>0,原不等式等价变形为f(x1)−f(x2)>−(x1−x2),即f(x1)+x1>f(x2)+x2.

设g(x)=f(x)+x,则

由题意,要证对任意x1,x2∈(0,+∞),且x1>x2,恒成立,即要证明g(x)在(0,+∞)上单调递增.

评注例3 是一种特定题型,同时也很常见.当不等式中的两个变量对称并且能够分离,不等式又是对两个变量在某区间恒成立,则可以利用函数单调性的定义将问题转化为单调性进行处理,从而将双变量x1,x2转化为单变量x,然后利用导数工具求解即可.从最终效果来说,对称分离,转化为函数单调性,实现了将两个变量化二为一.

4.指定主元,分二为一

例5已知函数f(x)=aex+b在(0,f(0))处的切线为x −y+1=0.

(1)求f(x)的解析式;

(2)设A(m,f(m)),B(n,f(n)),m < n,k表示直线AB的斜率.求证:f′(m)

分析虽然要证的不等式中两个变量是对称的,但是不能分离,也不能化为商或差的形式整体换元,此题可以尝试指定其中一个变量为主变量,另一个为参数,把问题当成一个变量来处理.

解析(1)因为(0,f(0))在切线x −y+1 = 0 上,则f(0)= 1,即切点为(0,1),而切点又在函数f(x)=aex+b的曲线上,则b=1.于是f(x)=aex+1,f′(x)=aex,由题意f′(0)=1,即a=1,所以f(x)=ex+1.

(2)f′(m)< k < f′(n)即变形得(n −m)em

令g(n)=(n−m)em−en+em=nem−en−mem+em,n > m,则g′(n)=em−en<0,所以g(n)在(m,+∞)上单调递减,故g(n)

令h(n)=en−em−(n −m)en=(1−n+m)en−em,n>m,则h′(n)=(m−n)en<0,所以h(n)在(m,+∞)上单调递减,故h(n)

综上,(n −m)em< en−em<(n −m)en,于是得证.

评注指定主元,利用这个变量构造函数处理完后,若还剩下另一个变量,则只需把剩下的这个变量作为函数变量进一步处理即可,如例5 中得g(n)< g(m),若g(m)不是0 而是关于m的式子,则把m作为变量继续证明这个关于m的式子小于0.可以看出,指定主元这种处理方法的根本出发点就是将两个变量分成主次,依次逐个击破,分而化解,在分开逐个处理的每一个过程中就都成了单变量问题,即谓之分二为一.

结束语

综上所述,求解二元变量问题的核心是转化成一元变量,这是数学中多元化一元的基本思想.上述的利用等量关系消元、整体换元(比值、差值)、对称分离变量,转化为单调性、指定主元,分开处理等求解方法,就是在这一思想的指导下,利用题目的特有条件将二元变量问题转化为一元变量问题的不同手段.不管题目如何变化,万变不离其宗,本质就是如何将二元转化为一元的问题!