调和点列及调和线束性质的证明与应用举例
首都师范大学附属回龙观育新学校(102208) 李路军 李洪景
常在资料上看到一些证明不完整的有关调和点列和调和线束性质的叙述,作为教师只有理清其本质,使用起来才能心明眼亮.本文给出的例子,让我们更清楚的洞穿题目的意图及本质,为我们的教学提供了坚实的基础.本文着重对椭圆中的调和点列及调和线束问题予以讨论,实际上所提及的性质在二次曲线系中都是成立的,可类比得出.
调和点列的定义若同一直线上四点G,A,H,B满足GA×HB=GB×AH,即,则称A,B调和分割线段GH或G,H调和分割线段AB,A,B,G,H为调和点列(G,H与A,B称为调和共轭).
一、完全四边形中的调和点列
1.完全四边形.两两相交又没有三线共点的四条直线段及它们的六点所构成的图形称作完全四边形,如图1,ABMCKD是一个完全四边形.
2.完全四边形中的调和点列.
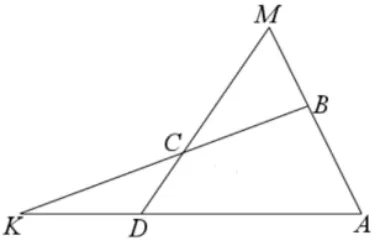
图1
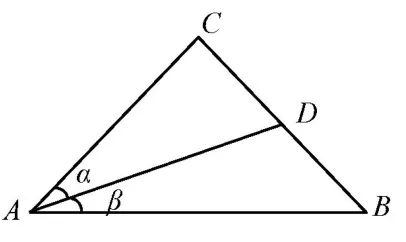
图2
作为准备,我们考虑如下张角定理:
张角定理[1](本质是正弦定理的面积形式).如图2,三角形ABC中,D为BC上一点,连接AD,设∠CAD=α,∠BAD=β,则
证明因为S∆ABC=S∆ABD+S∆ADC,所以两边同时除以AB·AC·AD,整理得:
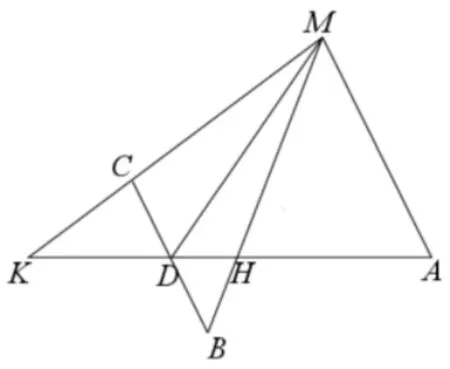
完全四边形中的调和点列[2]如图3.1,完全四边形ABMCKD中,设AC与BD的交点为G,连接MG交AD于H,则A,D,H,K为调和点列.
证明设 ∠MAC=α,∠KAC=β,在∆AMH,∆ABD,∆AMD,∆ABK中,分别有:
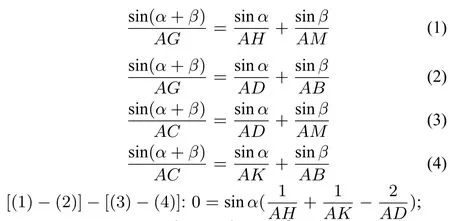
因为sin0,所以;所以
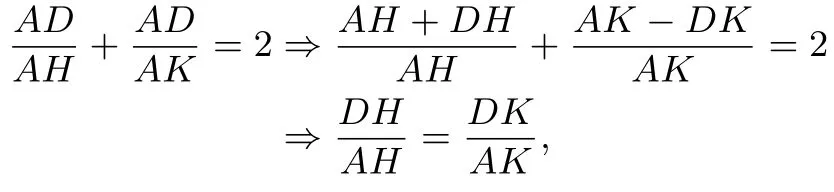
即AH ×DK=AK×DH,则A,D,H,K为调和点列.
根据线段间的数量关系,调和点列有不同的等价形式:
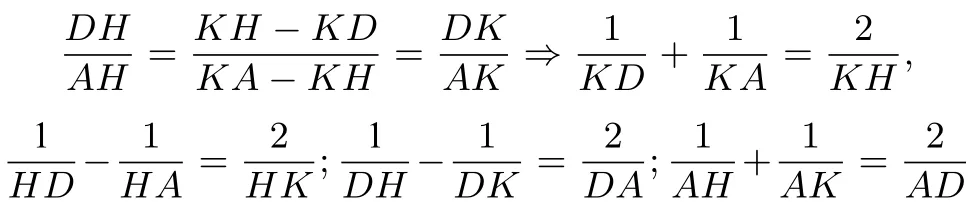
都可以说明点A,D,H,K为调和点列.
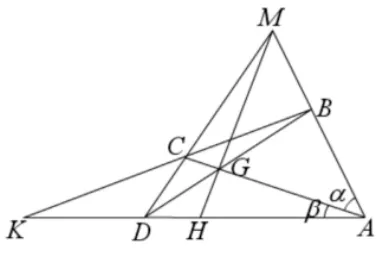
图3.1
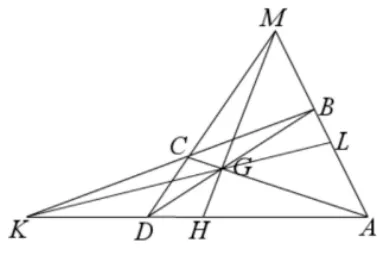
图3.2
如图3.2 连接KG交AM于L,则点A,B,L,M也为调和点列,这也正是本文要讲的调和线束性质2.图3.2 中有7 线9 点,存在四个完全四边形,这个图形也成为完全四点形[3].
二、圆锥曲线中的调和点列
圆、椭圆、双曲线、抛物线这个家族中,有很多共性,这里以椭圆为例证明.
性质1给定椭圆= 1(a > b >0),过点F(x0,y0)(F不在椭圆上且不为原点)的直线与椭圆交于A,B不同两点,若点P,F,A,B为调和点列,则点P为直线AB与直线的交点.
证明设A(x1,y1),B(x2,y2),P(m,n).当直线AB斜率存在时,设AB方程为y −y0=k(x −x0).与椭圆方程联立,化简得:
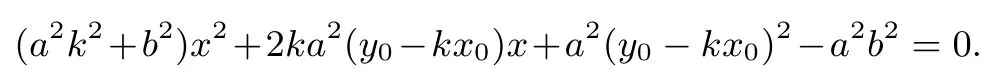
当∆≥0 时,
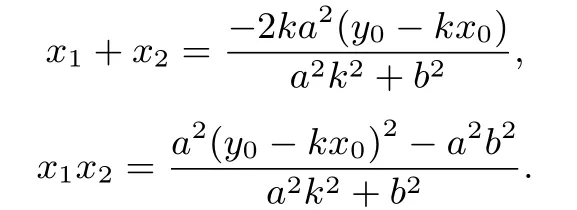
点P,F,A,B为调和点列,即满足即2mx0+2x1x2−(x0+m)(x1+x2)= 0;两根之和之积代入,化简得:a2y0(m −x0)k+(mx0b2+a2y20−a2b2)=0.又代入化简得即有P点在直线上.
如果过F的直线斜率不存在,且与椭圆也有两个不同的交点时,根据纵坐标间的关系,可验证P点也满足直线方程.
综上,P点恒在直线上.得证.
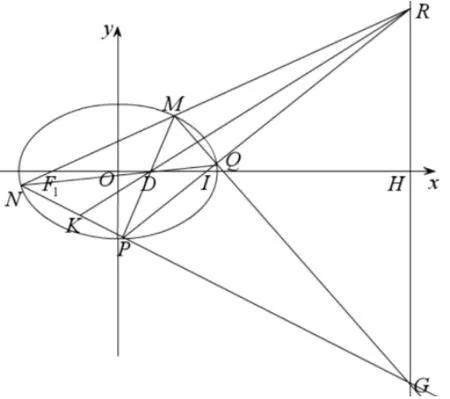
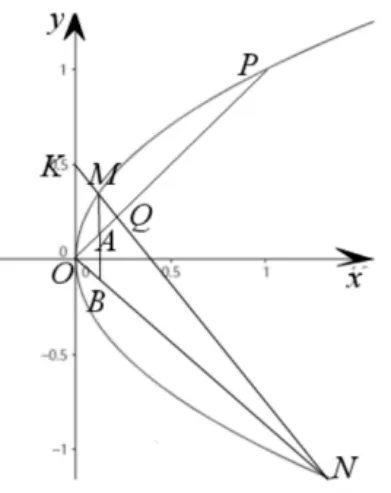
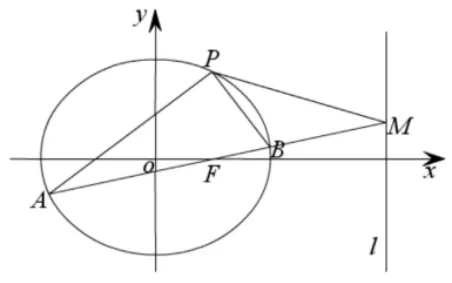
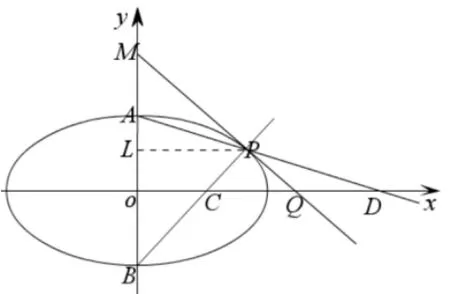
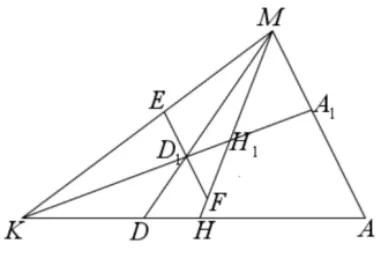
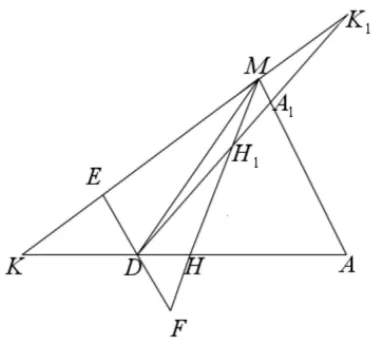
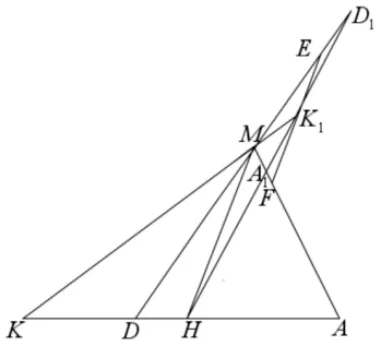
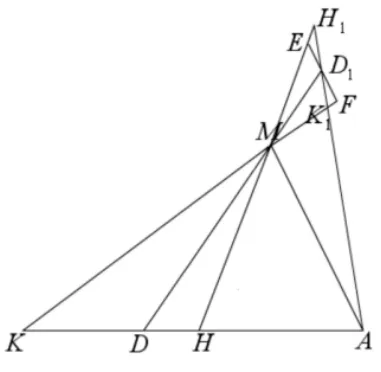
当点F为(t,0)(−a < t < a,t0)时,点P在直线上;点F为焦点时,点P在相应的准线上.当点F为(0,t)(−b 评注在射影几何中,直线称为点F(x0,y0)关于椭圆的= 1(a > b >0)极线,点F(x0,y0)称为直线的极点.从上面的证明过程可知,过点F(x0,y0)的直线与椭圆交于A,B不同两点,若点P,F,A,B为调和点列时,点P为直线AB与点F的极线的交点. 所以在圆锥曲线中,调和点列与曲线的极线极点相关. 调和线束的定义如图4,如果K,H,D,A是调和点列,直线外一点M与它们的连线称为调和线束,即直线MK,MH,MD,MA为一簇调和线束. 平面内不过点M也不与KA重合的直线,可以划分为两类,一类是与其中一条线束平行;一类是与四条线束都不平行,下面研究它们的性质. 图4 图5 调和线束性质1平面内若一条直线与调和线束中的其中一条平行而与其余三条相交,则相交线段被平分.下面仅以与MA平行进行证明. 如图5,过点D作MA的平行线,分别交直线MK,MH于点C,B,则D为线段CB中点. 证明:∆KDC~ ∆KAM,所以; 又∆DBH~∆AMH,所以;又因为K,H,D,A为调和点列,,所以CD=DB,即D为BC中点.则所有与MA平行的直线被MK,MD,MH所截,得到的线段被平分. 如果直线与MH平行,可以过点K作辅助线进行证明.其余类推. 调和线束性质2平面内若一条直线与调和线束都相交,且交于不同的四个点,则相应的交点也成调和点列.下面分四种情况进行证明. (1)直线与射线MK,MD,MH,MA都相交或者与其反向延长线都相交的情况.如图6,过点K作一条直线l与直线MD,MH,MA分别相交于点D1,H1,A1,则K,H1,D1,A1为调和点列. 证明过点D1作MA的平行线交MK,MH于E,F两点.根据性质1,可知D1为EF的中点. ∆KED1~ ∆KMA1,所以; 又∆D1FH1~∆A1MH1,所以,则K,H1,D1,A1为调和点列. 根据平行性,平面内与l平行的任意直线与调和线束相交后,相应的四个点也构成调和点列. 图6 图7.1 (2)直线与其中三条射线相交,与另一条射线反向延长线相交的情况.仅以与MK反向相交为例.如图7.1,过点D作一直线l与射线MK反向延长交于点K1,与MH,MA分别交于点H1、A1,则相应的点K1,H1,D,A1成调和点列. 证明过点D作MA的平行线交MK,MH于E,F两点.根据性质1,可知D为EF的中点. ∆K1ED~ ∆K1MA1,所以又∆DFH1~∆A1MH1,所以所以,则K1,H1,D,A1为调和点列. 根据平行性,平面内与l平行的任意直线与调和线束相交后,相应的四个点也构成调和点列. (3)直线与其中两条射线相交,与另两条射线反向延长线相交的情况.这里以与MK、MD反向相交为例.如图7.2,过点H作一直线l与射线MK、MD反向延长线交于点K1,D1,与MA交于A1,则相应的点K1,H,D1,A1成调和点列. 证明过点K1作MH的平行线交MD1,MA于E,F两点.根据性质1,可知K1为EF的中点. ∆K1ED1~ ∆HMD1,所以又∆A1FK1~∆A1MH,所以,则K1,H,D1,A1为调和点列. 根据平行性,平面内与l平行的任意直线与调和线束相交后,相应的四个点也构成调和点列. 图7.2 图7.3 (4)直线与其中一条射线相交,与其余三条射线反向延长线相交的情况.这里以与MA相交为例.如图7.3,过点A作直线l与射线MK、MD、MH反向延长线交于点K1,D1,H1,则相应的点K1,H1,D1,A成调和点列. 证明过点D1作MA的平行线交MH,MK的反向延长线于E,F两点.根据性质1,可知D1为E,F的中点. ∆H1ED1~ ∆H1MA,所以; 又∆D1FK1~∆AMK1,所以;所以,则K1,H1,D1,A为调和点列. 根据平行性,平面内与l平行的任意直线与调和线束相交后,相应的四个点也构成调和点列.综上,平面内任意一不过点M的直线都有相应的情况对应. 例1(2018年武汉大学自主招生试题[4])已知椭圆的左右焦点为F1,F2,A,B分别为椭圆E的左右顶点,D(1,0)为线段OF2的中点,且 (Ⅰ)求椭圆E的方程; (Ⅱ)若点M为椭圆E上的动点(异于A,B),连接MF1并延长交椭圆E于点N,连接MD、ND并分别延长交椭圆E于P,Q,连接PQ,设直线MN、PQ的斜率存在且分别为k1,k2,试问是否存在常数λ,使得k1+λk2= 0 恒成立?若存在,求出λ的值;若不存在,说明理由. 图8 简析(Ⅰ) (Ⅱ)如图8,点D对应的极线是x= 9,设NM、PQ交极线于点R,NP,MQ交极线于点G,则有完全四边形NMRQGP,连接RD,并延长交NPG于点K,则N,P,K,G为调和点列,RN,RP,RK,RG为调和线束,根据性质2,x轴与线束的相应交点依然为调和点列,设RQ与x轴的交点为I,极线与x轴的交点为H,即F1,D,I,H为调和点列,满足,把坐标代入,可得,则 图9 例2(2017年高考北京卷理科第18 题)已知抛物线C:y2= 2px过点P(1,1),过点作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP,ON交于点A,B,其中O为原点. (I)求抛物线C的方程; (II)求证:A为线段BM的中点. 简析(I)抛物线C的方程为y2=x; 例3(2013年高考江西卷理科)椭圆1(a>b>0)经过点,离心率,直线l的方程为x=4. (Ⅰ)求椭圆C的方程; (Ⅱ)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3.若存在求λ的值;若不存在,说明理由. 简析(Ⅰ) (Ⅱ)如图10,直线x= 4 是右焦点的极线,所以点M,F,B,A为调和点列,PM,PF,PB,PA为调和线束,由调和线束性质2,则x轴与调和线束相应的交点依然为调和点列,设PM,PB,PA与x轴的交点依次为K,R,X,则K,F,R,X为调和点列,有,则,化简kPA+kPB=2kPM. 图10 例4设A,B是椭圆短轴(长轴)的两个端点,P为平面内任意一点(不在直线AB上),设直线PA,PB与椭圆分别交于E,F,与长轴(短轴)所在直线分别相交于C,D,直线EF与短轴(长轴)所在直线相交于M,则直线PM平分线段CD[5]. 简析如图11,实际上,此试题可认为是过y轴上一点M(不与原点、A,B重合)作直线交椭圆于E,F,连接AE,BF,相交于一点P,则直线PE,PM,PF被x轴所截,截得的线段被平分. 图11 设BE与AF的交点与点P的连线与y轴的交点为L,在完全四边形BFPEMA中,M,L,A,B为调和点列,PM,PL,PA,PB为调和线束,又点M在y轴上,其极线PL一定与y轴垂直,根据调和线束性质1,那么x轴与另外三条线束的相交线段被平分. 图12 如果点P在椭圆上(不与顶点重合),如图12,设过点P的切线与x轴交于Q点,M,L,A,B为调和点列,PM,PL,PA,PB为调和线束,根据调和线束性质1,那么x轴与另外三条线束的相交线段被平分,则Q为CD中点. 本文仅仅是对圆锥曲线中的椭圆进行了相应的研究,而在圆、双曲线、抛物线中也是成立的. 圆锥曲线压轴题,一向都是思维的难点与计算的痛点,但是如果能先从几何的角度去认识它,分析它,就有助于对习题的深刻理解,并减少运算.所以人们常说,解析几何首先是几何,要有几何的眼光.调和线束的性质应用,在一些竞赛中也常常隐蔽出现[6],只有掌握了其本质,解决问题时才能直入主题,才能站在高处思考问题,故以后的教学中,要有意的培养学生洞察问题本质的意识,不仅仅是“解析”.如果不能从几何角度解释,说明我们还没有找到几何解释的方法.三、调和线束的两条性质

四、应用举例