一道几何赛题的探究与推广

广东省深圳中学(518001) 邱际春

1 问题提出

著名数学家华罗庚先生在《1978年全国中学生数学竞赛题解》一书的前言中提到了下面一道具有丰富内涵的几何题:

题目[1]若凸四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC延长后分别与直线KL交于点F,G.求证:

华罗庚先生指出这个问题包含了射影几何的基本原理,从结论可以看出,给定K,F,L三点时,可以仅用直尺作图便可找出点G,使得F“内分”KL的比例,等于G“外分”KL的比例.张景中院士在《几何新方法和新体系》[1]与《从数学教育到教育数学》[2]中均摘录了这一问题,并对此作了深入地分析,提出了以共边定理为基础的多种解法.

笔者在“巨人”的肩膀上对这一几何问题进行多角度探究,得到一些有意义的结论.

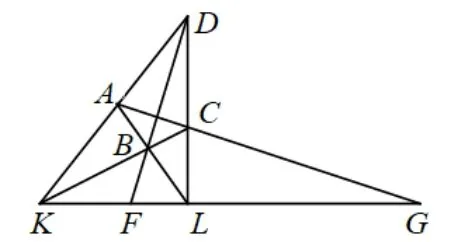
图1

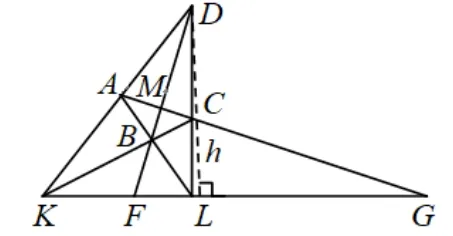
图2

2 解法探究

首先,我们来看华罗庚给出的用中学生所掌握的知识可以解决的方法.

证法1如图2,设∆KFD中KF边上的高为h,利用2S∆KFD=FK · h=DF · DKsin ∠FDK,可得进而再求出与的类似表达式.于是

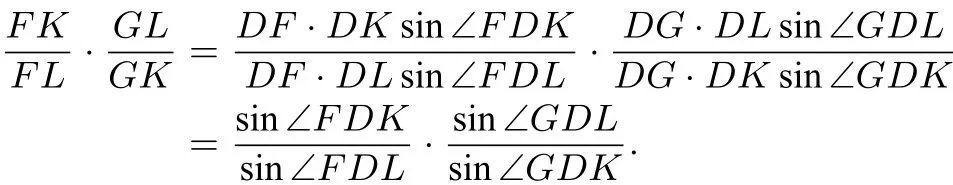
类似地,有

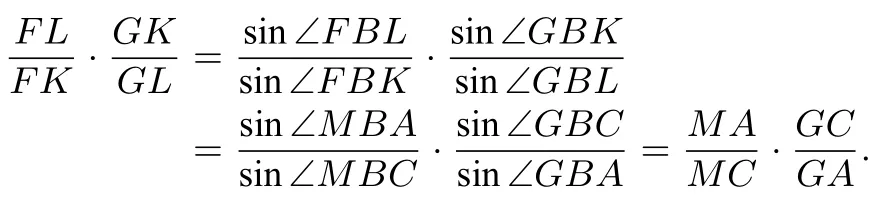
评注事实上,若读者熟悉三角形的又一面积公式

也容易证得这一结论.

其次,考虑到题目中涉及直线的相交和同一直线上的线段比,故可用共边定理将线段比化为面积比,把面积比化为线段比,在两种几何量的反复转化中解决问题.

证法2由共边定理可得

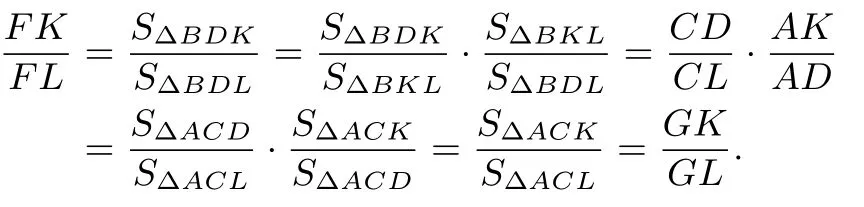
评注显然,上述证法非常简明.若考虑适当添加辅助线后亦可证得,例如在图3中连接CF,则有

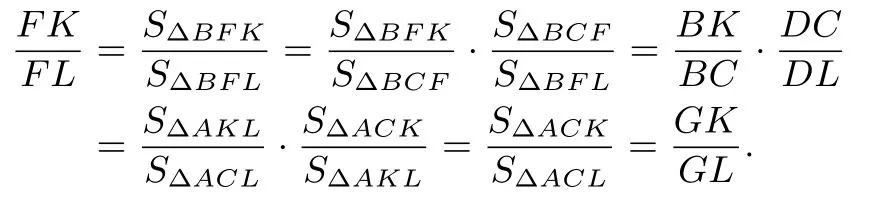
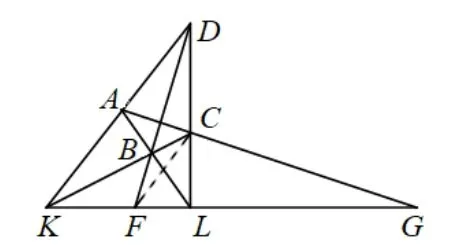
图3

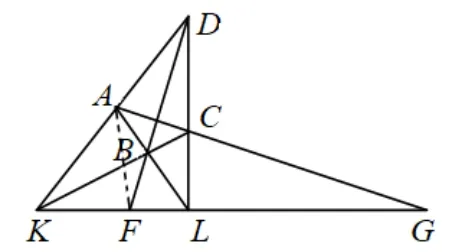
图4

在图4中连接AF,则有

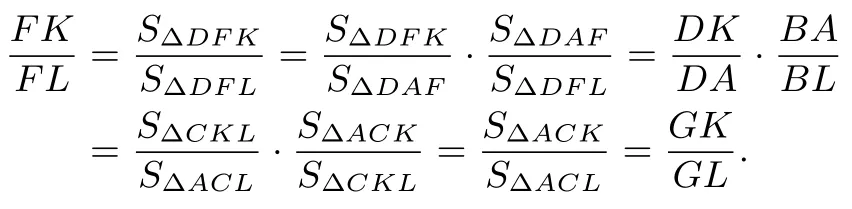
最后,容易看出图形中隐含“三线共点”和“三点共线”的条件,故可直接用塞瓦定理和梅涅劳斯定理进行转化.

证法3注意到对于点B与∆DKL,应用塞瓦定理可得对于直线AG截∆DLK,截点依次为A,C,G,应用梅涅劳斯定理可得

评注在数学竞赛试题中,当题设条件或所证结论涉及“三点共线”与“三线共点”时,常常利用梅涅劳斯定理和塞瓦定理来解决.

3 变式探究

由于上述几何问题所要证的K,F,L,G是同一直线上的四个点,而图形中这样的点还有很多,例如D,M,B,F;A,M,C,G,以及延长BC与DG交于点N的K,B,C,N,等等.因此,我们对上述几何问题进行探究,可以得到下面几个变式题.

变式1若凸四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC相交于点M,且对角线BD,AC延长后分别与直线KL交于点F,G.求证:

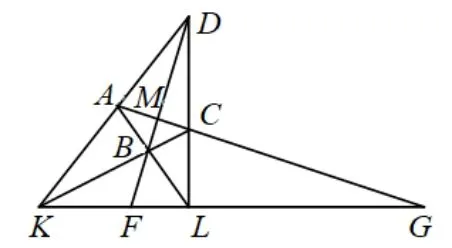
图5

证法1由共边定理可得

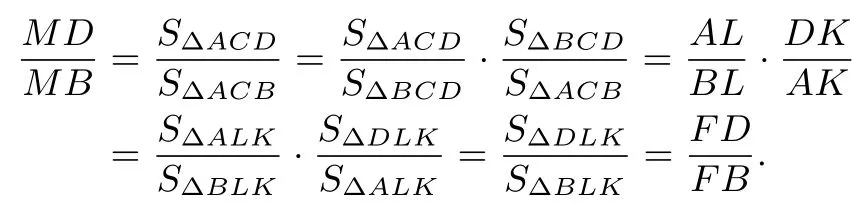
证法2注意到对于点C与∆ABD,应用塞瓦定理可得对于直线KL截∆ABD,截点依次为K,F,L,应用梅涅劳斯定理可得

变式2若凸四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC相交于点M,且对角线BD,AC延长后分别与直线KL交于点F,G.求证:

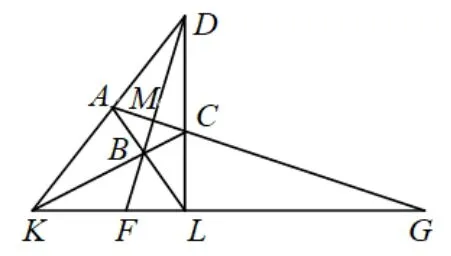
图6

证法1由共边定理可得

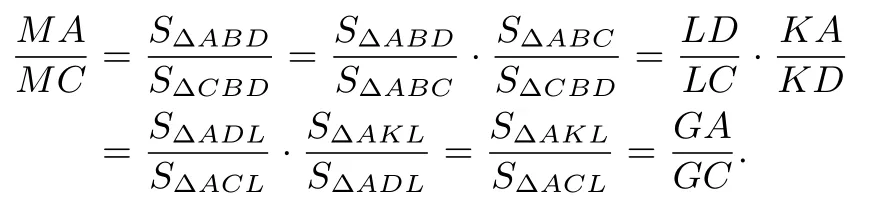
证法2注意到对于点B与∆ACD,应用塞瓦定理可得对于直线KG截∆ACD,截点依次为K,L,G,应用梅涅劳斯定理可得

变式3若凸四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC延长后分别与直线KL交于点F,G,边BC延长后与直线DG交于点N.求证:

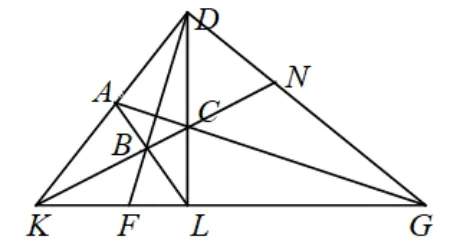
图7

证法1由共边定理可得

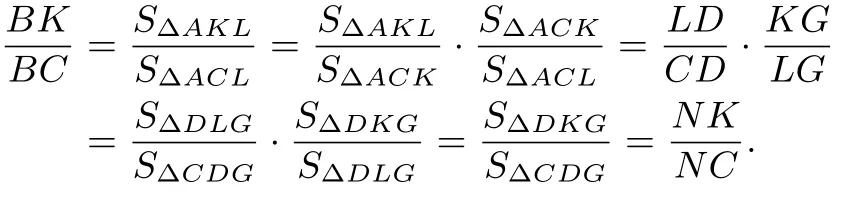
证法2注意到对于点A与∆CKL,应用塞瓦定理可得对于直线DG截∆CKL,截点依次为D,N,G,应用梅涅劳斯定理可得

评注事实上,上述变式题也可用面积法和消点法来解决.此外,连接BG分别交直线DK,DL于点P,Q,还有等结论.

4 拓展延伸

4.1 直接推广

考虑到凸四边形只是较为特殊的一种平面四边形,相应的还有凹四边形和星形四边形,故可将凸四边形推广至平面四边形,从而得到下面的几何问题.

推广1若平面四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC延长后分别与直线KL交于点F,G.则有

分析若平面四边形ABCD是凸四边形,则证明方法同原题目;若平面四边形ABCD是凹四边形(如下图8),则证明方法同变式2;若平面四边形ABCD是星形四边形(如下图9),则证明方法同变式1.

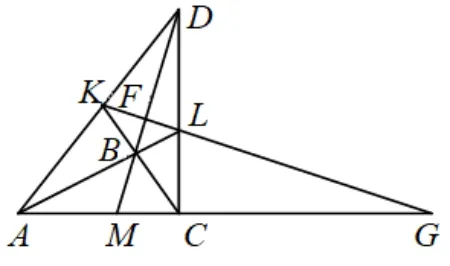
图8

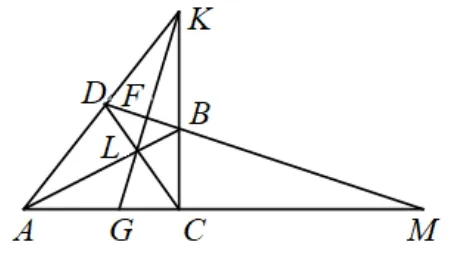
图9

推广2若平面四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC相交于点M,且对角线BD,AC延长后分别与直线KL交于点F,G.则有

推广3若平面四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC相交于点M,且对角线BD,AC延长后分别与直线KL交于点F,G.则有

推广4若平面四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC相交于点M,且对角线BD,AC延长后分别与直线KL交于点F,G,边BC延长后与直线DG交于点N.则有

评注事实上,推广1 至推广3 相互等价,而推广4 的证明也大同小异,故留给读者思考,不再赘述.

4.2 利用调和点列的性质进行拓展

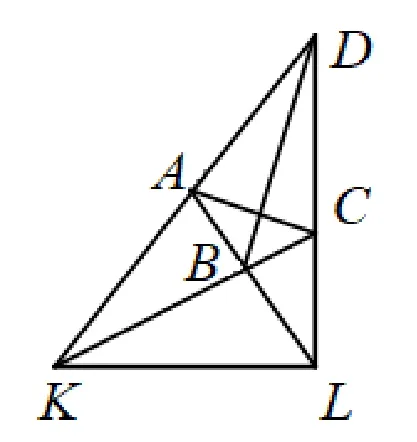
图10

我们观察图1发现,其中蕴含下面一个基本图形——完全四边形.这是由两两相交且没有三线共点的四条直线及它们的六个交点所构成的图形,如图10.与完全四边形联系紧密的是调和点列,这涉及到线段的内分点与外分点,我们设两点C,D内分与外分同一线段AB成同一比例,即则称点C和D调和分割线段AB,或者A,B,C,D是调和点列.因此,原题目中K,L,F,G成调和点列,变式1 至变式3 中的A,C,M,G;D,B,M,F;K,C,B,N均为调和点列.

接下来,我们介绍有关调和点列的两个性质[3]:

性质1若A,C,B,D是共线的四点,则C,D调和分割线段AB的充要条件是AB·CD=2AD·BC=2AC·BD;

性质2若A,C,B,D是共线的四点,过共点直线外一点O引射线OA,OC,OB,OD,则C,D调和分割线段AB的充要条件是另一直线l分别交射线OA,OC,OB,OD于点A′,C′,B′,D′,点C′,D′调和分割线段A′B′.

根据上述两个性质,可进一步探究得到下面两个结论:

推广5若凸四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,对角线BD,AC相交于点M,且过点M的直线分别交AD,BC,KL于点P,Q,G.则有

分析如图11,延长BD与KL交于点F,且连接KM.注意到过点K的四条线束KD,KM,KC,KL均被两条直线DF,PG所截.又由变式1 的结论可知D,B,M,F成调和点列,从而由性质2 知P,Q,M,G是调和点列,故

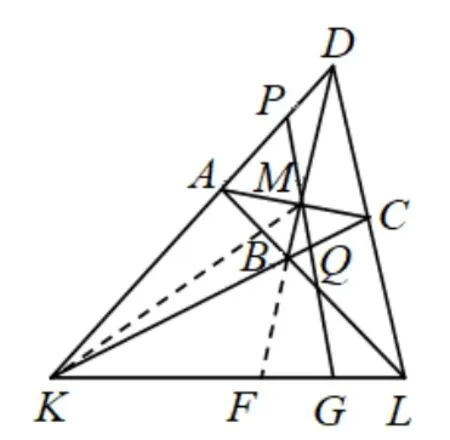
图11

评注特别地,当直线PG绕着点M顺时针旋转至与DF重合时,推广5 便退化为变式1.

推广6若凸四边形ABCD的两边AD,BC延长后交于点K,两边AB,CD延长后交于点L,过点D的直线分别交AC,AL,CK,KL于点E,F,P,Q,延长KL,AC交于点G,延长GB分别交DL,DQ于点H,I.则有

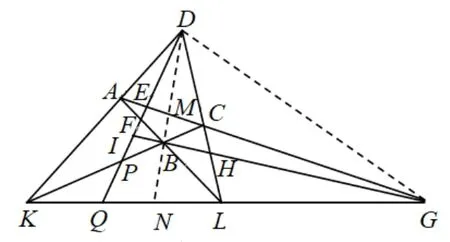
图12

分析如图12,延长BD分别交AC,KL于点M,N,连接DG,则由变式1 可知故D,B,M,N成调和点列.考虑过点G的四条直线GD,GA,GF,GK分别与直线DN,DQ交于点D,M,B,N和点D,E,I,Q,从而由性质2 知D,I,E,Q成调和点列,故由性质1 可得DI ·EQ=2DQ·IE=2ED·QI.

同理可知,K,L,N,G成调和点列,考虑过点B的四条直线BK,BN,BL,BG分别与直线AG,DQ交于点K,N,L,G和点P,D,F,I,从而由性质2 知P,F,D,I成调和点列,故由性质1 可得PF ·DI=2PI·FD=2PD·FI.

由上述两式可得

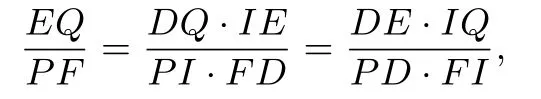
从而

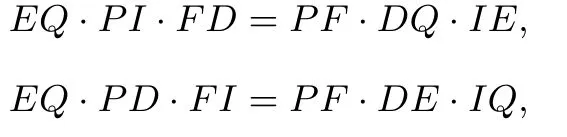
故

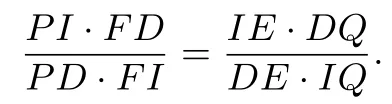
评注特别地,当直线DQ绕着点D逆时针旋转至与DB重合时,则推广6 退化为变式1.