从2019年浙江卷解几压轴题谈两三角形面积之比的求解策略*

福建省龙海第一中学新校区 苏艺伟

福建省漳州漳浦第四中学 陈锦山

一、试题呈现

题目(2019年浙江卷理科解几压轴试题)如图1,已知点F(1,0)为抛物线y2= 2px(p>0)的焦点.过点F的直线交抛物线于A,B两点,点C在抛物线上,使得∆ABC的重心G在x轴上,直线AC交x轴于点Q,且Q在点F的右侧.记∆AFG,∆CQG的面积分别为S1,S2.

(1)求p的值及抛物线的准线方程;(2)求的最小值及此时点G的坐标.

图1

二、试题分析

在文[1]中,林国红老师对此题的第二步进行了探究,给出了两种解法,并将结论推广.两种解法中计算∆AFG和∆CQG面积都是采用底乘以高除以2 的方法,在运算量上偏大.试题第二步要求的是∆AFG和∆CQG面积之比的最小值.观察图形,分析图中几何要素中隐含的几何关系.不难发现,可以借助平面几何知识求解.∆ABC的重心G告诉我们S∆ABG=S∆ACG.从图1不难发现,S1和S∆ABG存在一定的关系,S2和S∆ACG存在一定的关系,只要能够把它们的关系研究清楚,本题就顺利求解.

不妨设A(x1,y1),B(x2,y2),C(x3,y3)

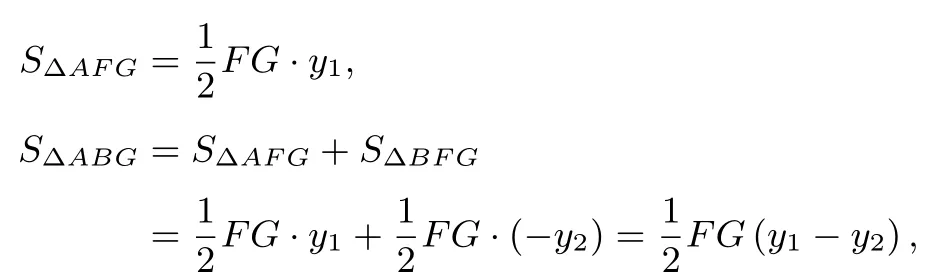
所以∆ABG和∆AFG都是以FG为底,面积之比为高之比,即.同理

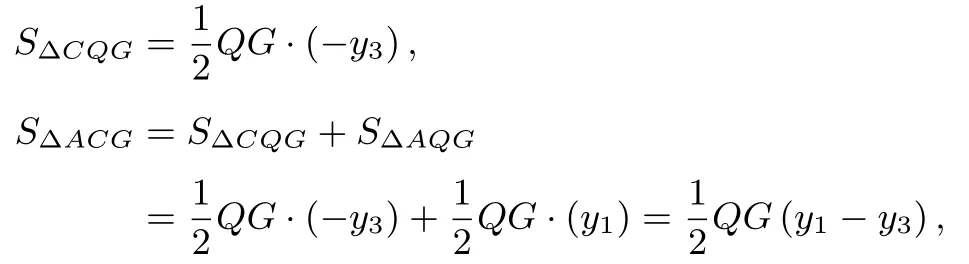
所以∆CQG和∆ACG都是以QG为底,面积之比为高之比,即

又由于S∆ABG=S∆ACG,从而可以得到的表达式.

三、试题解析

解析(2)由第一步知抛物线方程为y2= 4x.设A(x1,y1),B(x2,y2),C(x3,y3).y1+y2+y3= 0,y3=−y1−y2.从而

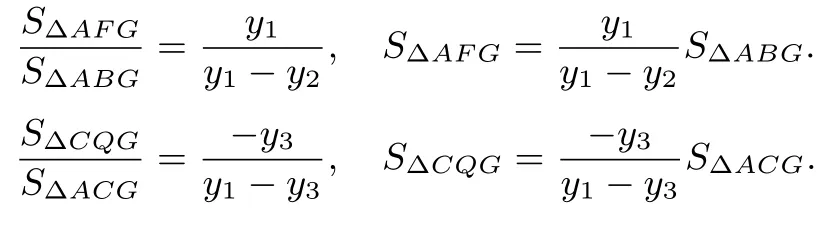
故

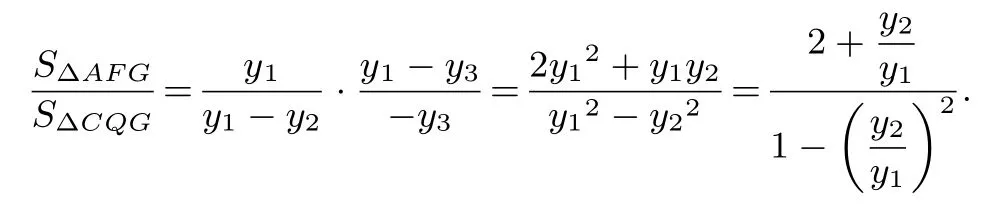
令f′(t)=0,得在单调递减,在单调递增.

因此,f(t)的最小值为所以的最小值为

四、试题方法总结

本题求解的关键在于借助平面几何知识准确地表示出相关三角形的面积或者面积之比.通过观察图形不难发现∆ABG和∆AFG都是以FG为底,则面积之比为高之比;∆CQG和∆ACG都是以QG为底,面积之比也为高之比.这些几何关系的挖掘是建立在求三角形面积的平面几何知识基础之上,用到了“两三角形如果同底,则面积之比为高之比”这样的几何结论.因此,借助三角形面积的平面几何知识求解此类面积之比问题至关重要.

五、方法归纳

类型1:两个三角形同底,则面积之比为高之比

例1如图2,过点P(1,0)作两条直线x= 1 和l分别交抛物线y2=4x于A,B和C,D(其中A,C位于x轴的上方,l斜率大于零).直线AC,BD交于Q.

(1)求证点Q在定直线上.(2)若,求λ的最小值.

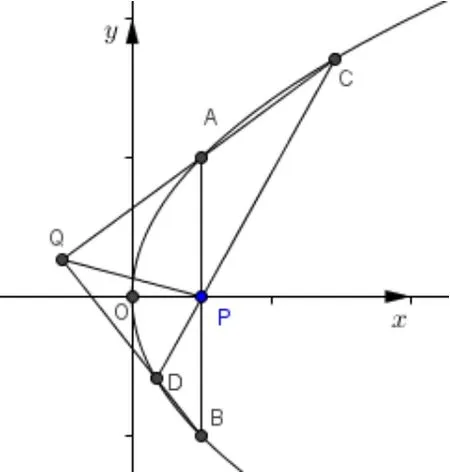
图2

解析由已知可得A(1,2),B(1,−2).设直线CD:x=my+1,m>0.设

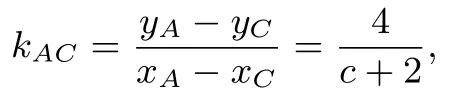
从而

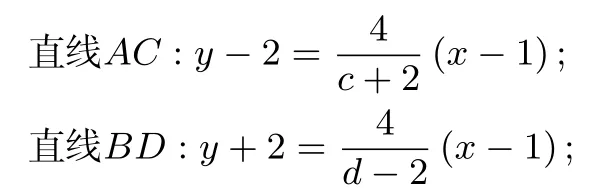
所以

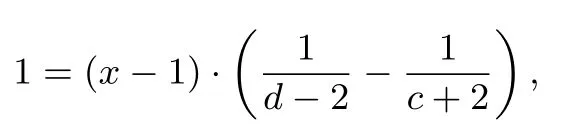
(2)因为

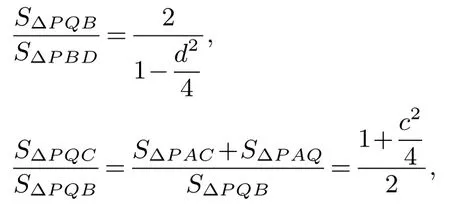
所以

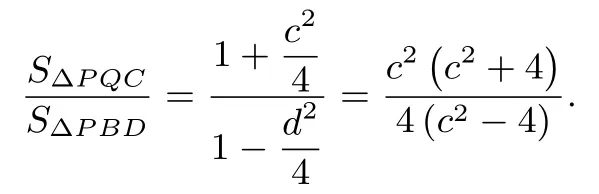
令c2−4=t,则t>0.所以

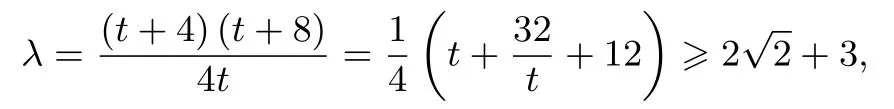
注记∆PQB和∆PBD同底,都是以PB为底,所以面积之比为高之比,即

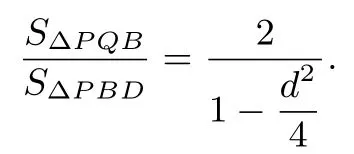
∆PAC和∆PAQ都是以AP为底,其面积之和为,即而∆PQB以PB为底,由于AP和PB相等,所以可视为∆PQC和∆PQB同底,都是以PB为底,所以面积之比为高之比,即

类型2:两个三角形等高,则面积之比为底之比

例2如图3,过抛物线y2=2px(p>0)上一点P作抛物线的切线l交x轴于Q,F为抛物线的焦点.以原点O为圆心的圆与直线l相切于点M.

(1)当P变化时,求证为定值.(2)当P变化时,记三角形PFM的面积为S1,三角形OFM的面积为S2,求的最小值.

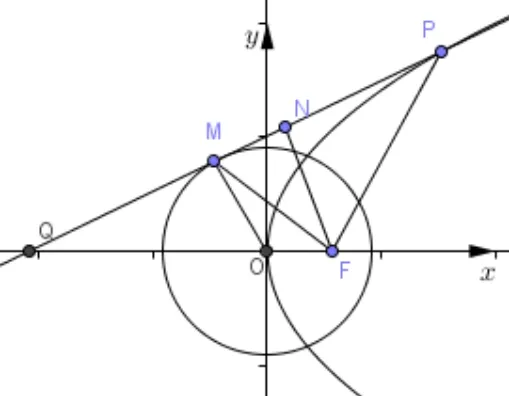
图3

解析(1)设P(x0,y0),则切线l方程为yy0=p(x+x0).令y= 0,得x=−x0,所以Q(−x0,0).则所以|QF|=|PF|,即

(2)由(1)知三角形PFQ为等腰三角形.取PQ中点N,则FN⊥PQ,OM//FN.设三角形MQF的面积为S3,OQ=t.则

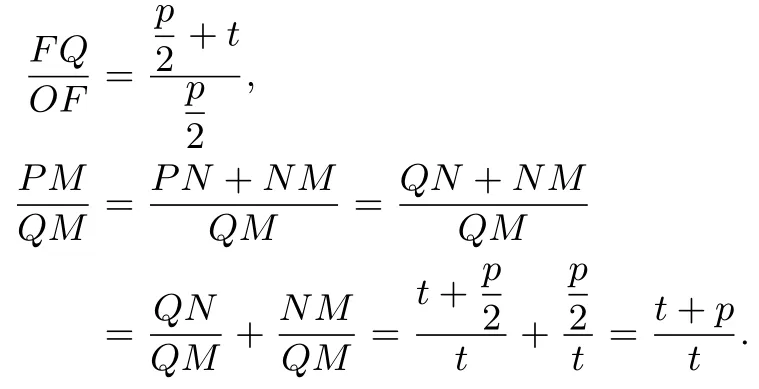
注记∆PFM和∆MQF等高,所以∆MQF和∆OFM等高,所以

例3(2013年高考湖北卷理科第21 题)如图4,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m > n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D.记∆BDM和∆ABN的面积分别为S1和S2.

(1)略.(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2? 并说明理由.

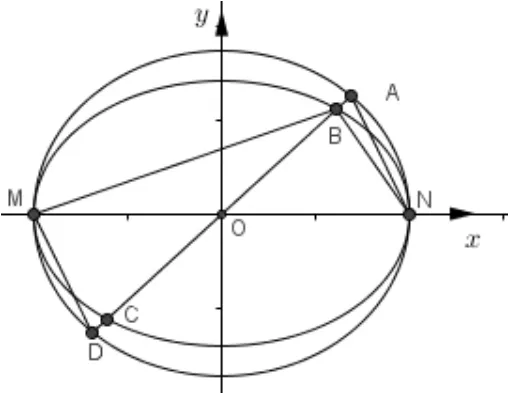
图4

解析设直线l的倾斜角为θ,则θ ∈(0,π),且,设OA=R,OB=r,则A(Rcosθ,Rsinθ),B(rcosθ,rsinθ).由已知有两式相减,得所以

注记∆BDM和∆ABN等高,所以

类型3:两个三角形相似,则面积之比为边长之比的平方

例4如图5,已知抛物线x2= 4y,F为其焦点,椭圆F1,F2为其左右焦点,离心率过F作x轴的平行线交椭圆于P,Q两点,

(1)求椭圆的标准方程;(2)过抛物线上一点A作切线l交椭圆于B,C两点,设l与x轴的交点为D,BC中点E,BC的中垂线交x轴于K,∆KED,∆FOD的面积分别为S1,S2,若且点A在第一象限,求A坐标.

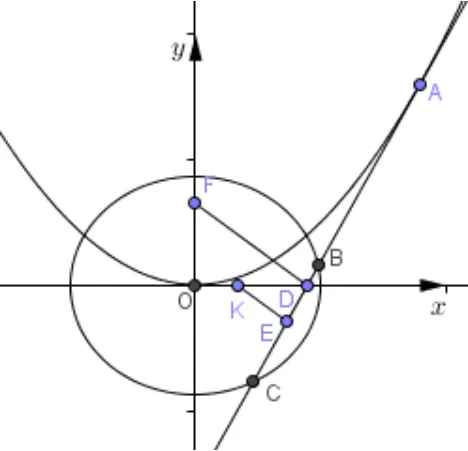
图5

解析(1)

设B(x1,y1),C(x2,y2),E(x3,y3).则

KE的方程:

令y= 0 得在直线l方程中,令y=0 得

注记∆DEK相似于∆FOD,所以

练习1如图6,过抛物线C:y=x2上的一点A(1,1)作抛物线的切线,分别交x轴于点D,交y轴于点B,点Q在抛物线上,点E,F分别在线段AQ,BQ上,且线段QD与EF交于点P.

(1)当点P在抛物线上,且时,求直线EF的方程;(2)当λ+µ=1 时,求S∆PAB:S∆QAB的值.

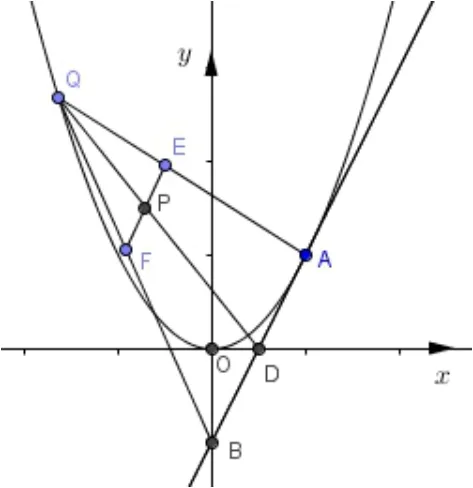
图6

解析(1)因为所以EF//AB.由y=x2得y′= 2x,故直线AB斜率为2,所以直线AB方程为y=2x −1.则

设Q(t,t2),P(x,y),由得代入y=x2得或者所以直线EF方程为或者

(2)由第(1)步知D为AB中点,所以由得

由Q,P,D三点共线可得由E,P,F三点共线可得

练习2已知抛物线C:x2=ay的图象经过点(2,1).

(1)求抛物线C的方程和焦点坐标;(2)直线l交抛物线C于A,B不同的两点,且A,B位于y轴的两侧,过A,B分别作抛物线C的两条切线交于点P,直线AP,BP与x轴的交点分别记作M,N.记∆ABP的面积为S1,∆ANP的面积为S2,∆BMP的面积为S3,试问是否为定值.

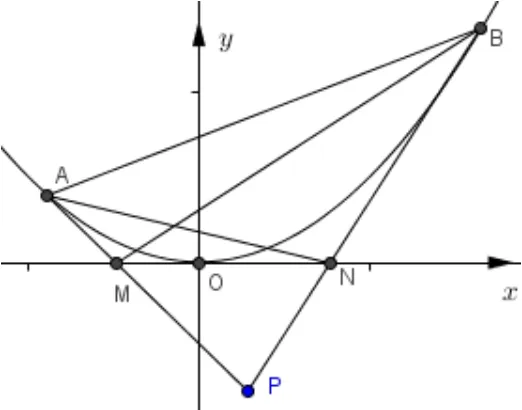
图7

解析(1)x2=4y,F(0,1).

(2)设直线AB方程为x=my+t,代入x2= 4y得m2y2+(2mt −4)y+t2=0.

设A(x1,y1),B(x2,y2),则

抛物线C在点A处的切线方程为

抛物线C在点B处的切线方程为

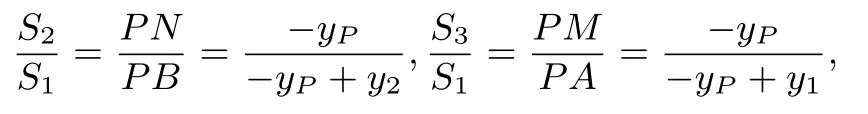
两式相加,得

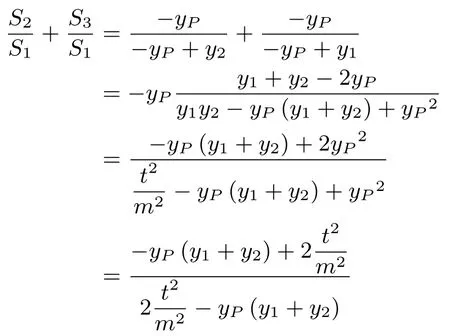
注记∆ABP与∆ANP等高,面积之比为底边之比,即;∆ABP与∆BMP等高,面积之比为底边之比,即

六、教学启示

通过上面的分析,不难发现解析几何压轴试题中的此类两三角形面积之比问题,求解策略是运用三角形面积的平面几何知识.由此可见平面几何知识的重要作用.几何是学生在初中就已经接触到的知识.学生在初中就已经学习了平面几何的一些性质,再加上高中几何知识的补充与强化,学生有了较为全面的平面几何知识,较好的应用平面几何的能力.因此,在解决圆锥曲线的相关问题中,如果我们能够将平面几何的知识应用上去,抓住解析几何问题的本质特征“几何性”,结合圆锥曲线的定义进行求解,那么可以使问题的解决变得清爽简明,自然简约,收到事半功倍的效果.